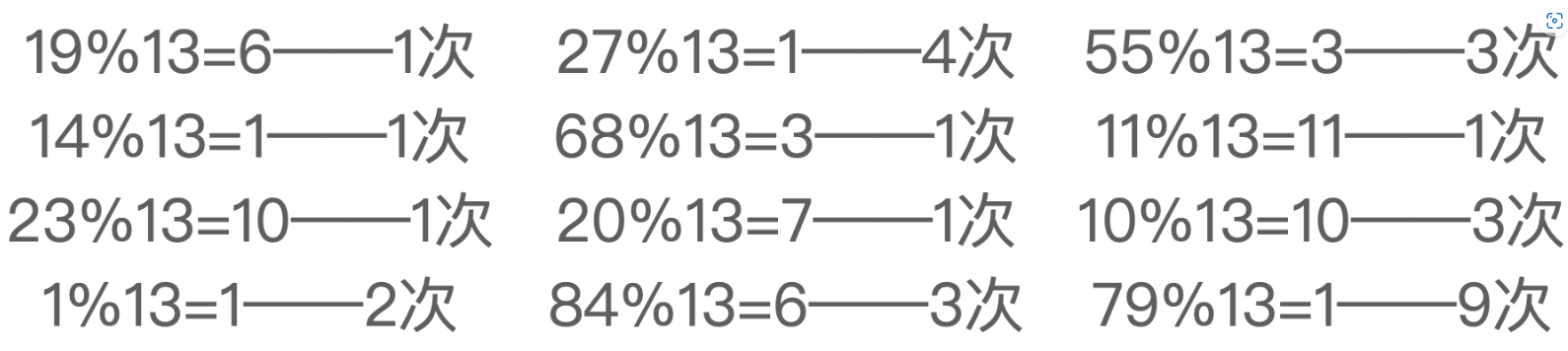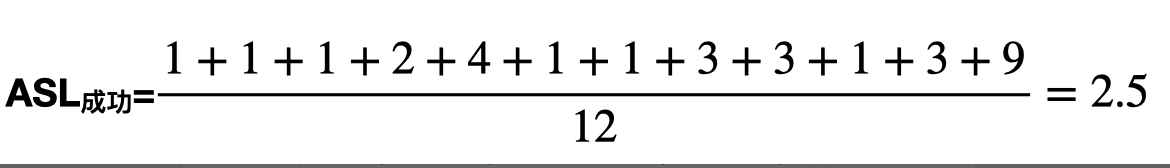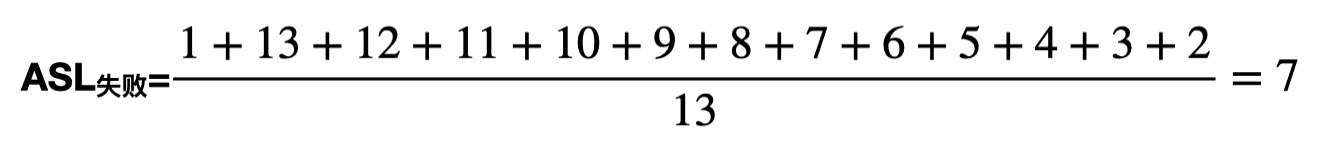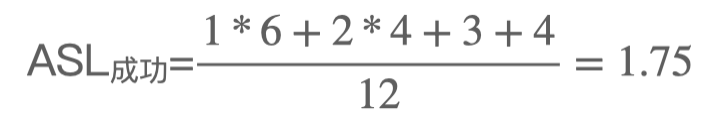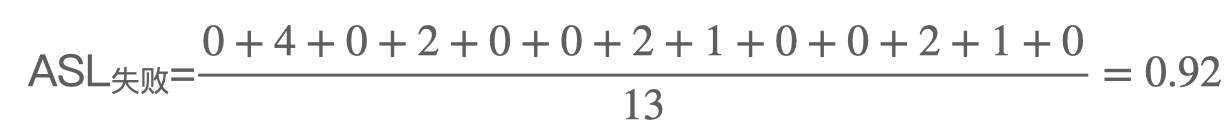数据结构打卡
树的应用
二叉树的定义、性质、画图
总结二叉树的度、树高、结点数等属性之间的关系
通过王道书 5.2.3 课后小题来复习“二叉树的性质”
定义顺序存储的二叉树–下标从1开始
二叉树顺序存储的数据结构定义,需要注意以下两点:
1 .二叉树的结点用数组存储,每个结点需要标记“是否为空”
2.各结点的数组下标隐含结点关系,要能根据一个结点的数组下标 i,计算出其父节点、左孩子、右孩子的数组下标
1 | 若顺序二叉树从数组下标1开始存储结点,则: |
1 | typedef struct TreeNode { |
实现函数,找到结点 i 的父结点、左孩子、右孩子
1 | //判断下标为 index 的结点是否为空 |
利用上述三个函数,实现先/中/后序遍历
1 | //从下标为 index 的结点开始先序遍历 |
定义顺序存储的二叉树(从数组下标0开始存储)
1 | 与 上面思路相同,只不过结点编号的计算有些区别而已 |
定义链式存储的二叉树
1 | //二叉树的链表结点 |
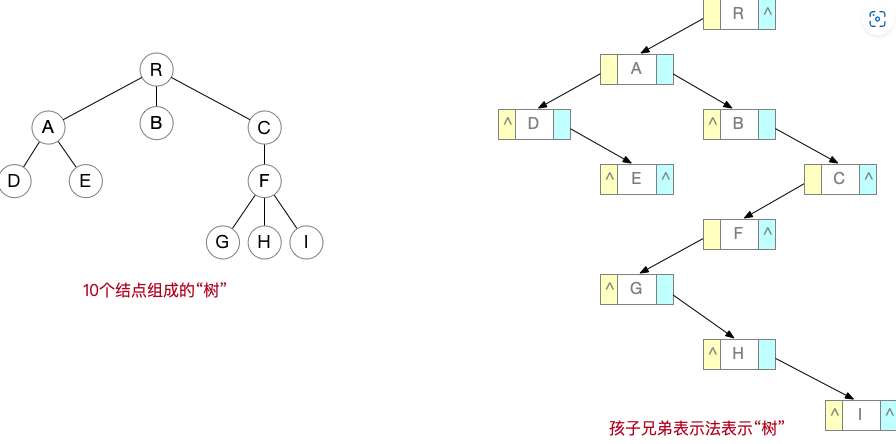
使用“孩子兄弟表示法”,定义链式存储的树(以及森林)
1 | typedef struct CSNode{ |
树的性质
总结树的度、树高、结点数等属性之间的关系
通过王道书 5.1.4、5.4.4 课后小题来复习“树和森林的性质”
树的定义、性质、画图
并查集的应用
实现并查集的数据结构定义,并实现 Union、Find 两个基本操作
1 |
|
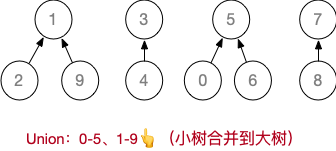
可采取“小树合并到大树”的策略优化 Union操作
1 | //Union “并”操作,小树合并到大树 |
可采取“路径压缩”的策略优化 Find 操作
1 | //Find “查”操作优化,先找到根节点,再进行“压缩路径” |
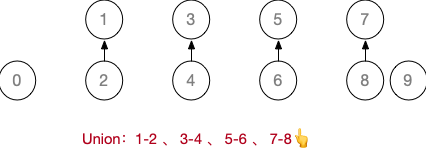
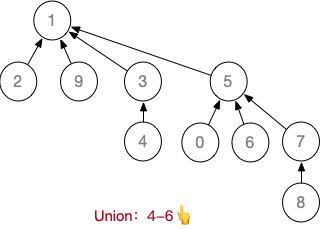
设计一个例子,对10个元素 Union
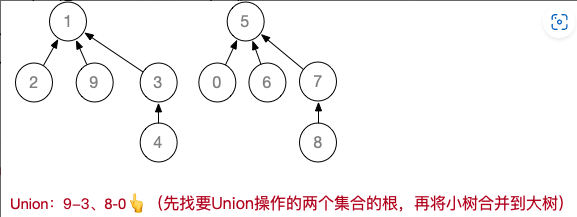
假设初始长度为 10 ( 0 ~ 9 )的并查集,按 1-2、3-4、5-6、7-8、 0-5 、1-9、9-3、8-0、4-6 的顺序进行Union操作
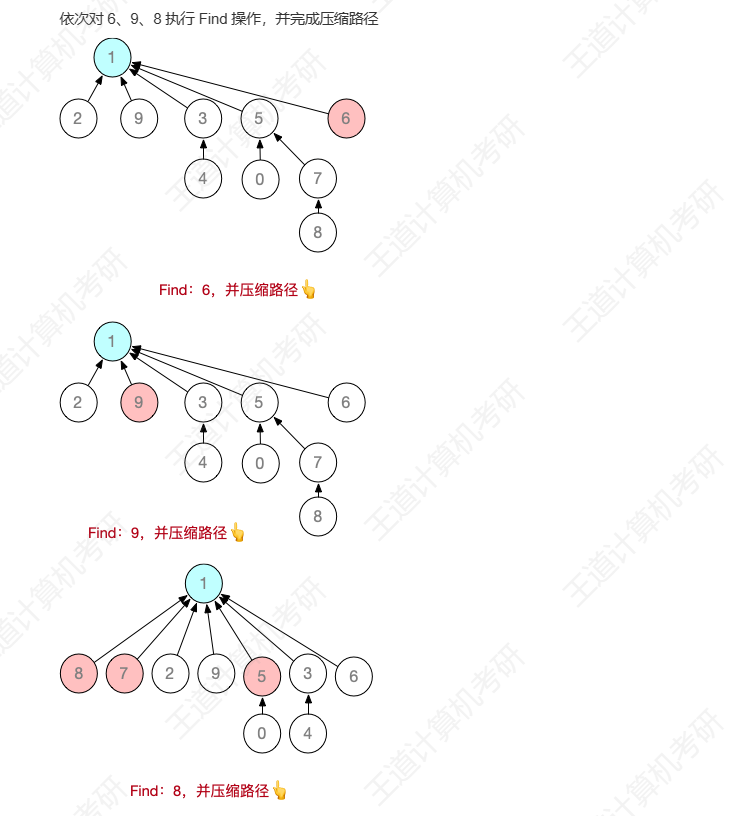
基于上述例子,进行若干次 Find,并完成“压缩路径”
图的应用
图数据结构的定义
写代码:定义一个顺序存储的图(邻接矩阵实现)
1 |
|
写代码:定义一个链式存储的图(邻接表实现)
1 |
|
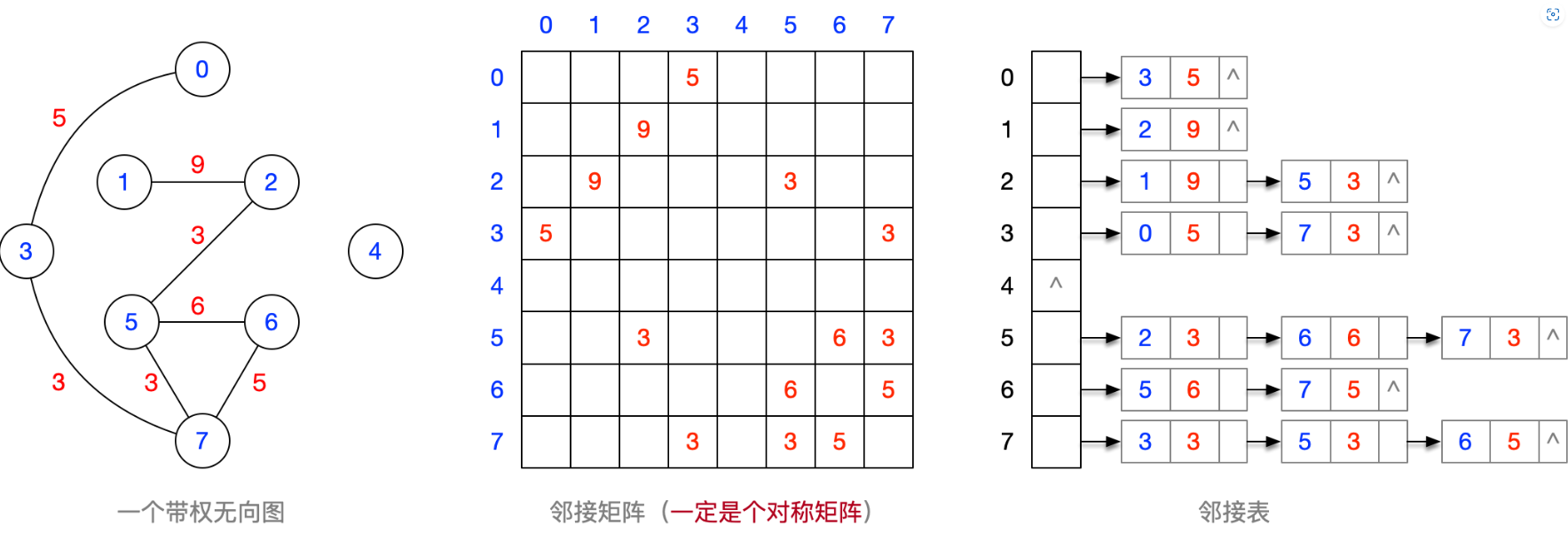
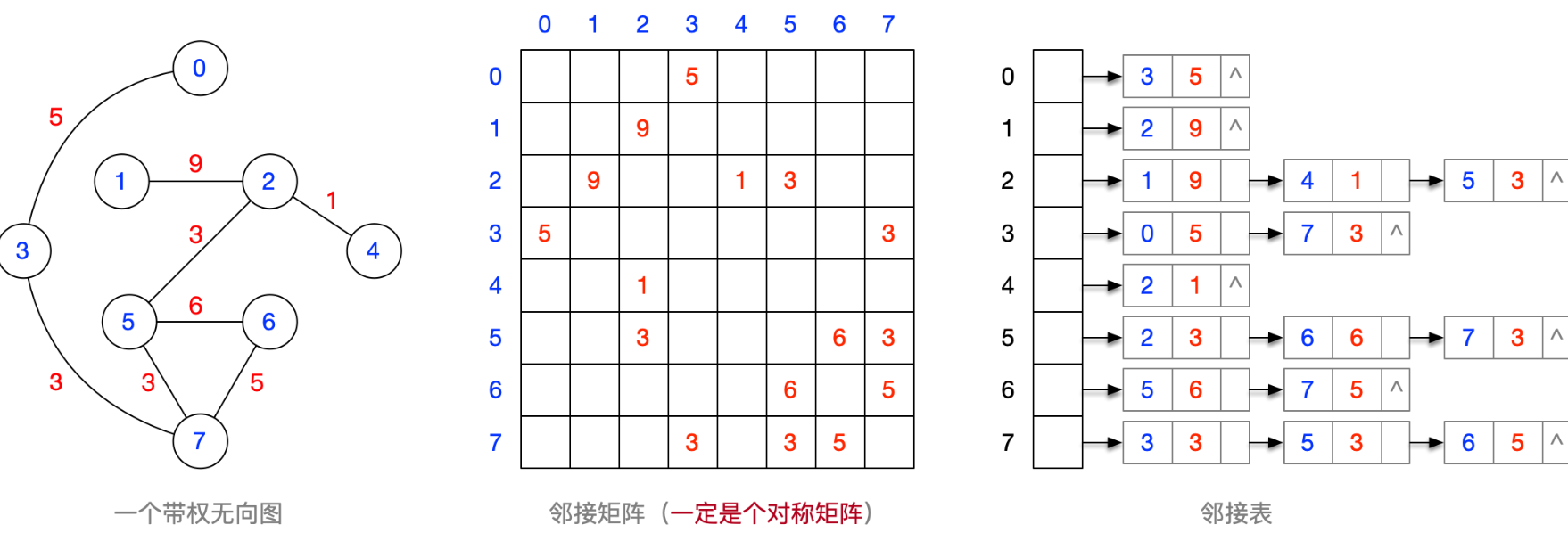
自己设计一个不少于6个结点的带权无向图,并画出其邻接矩阵、邻接表的样子
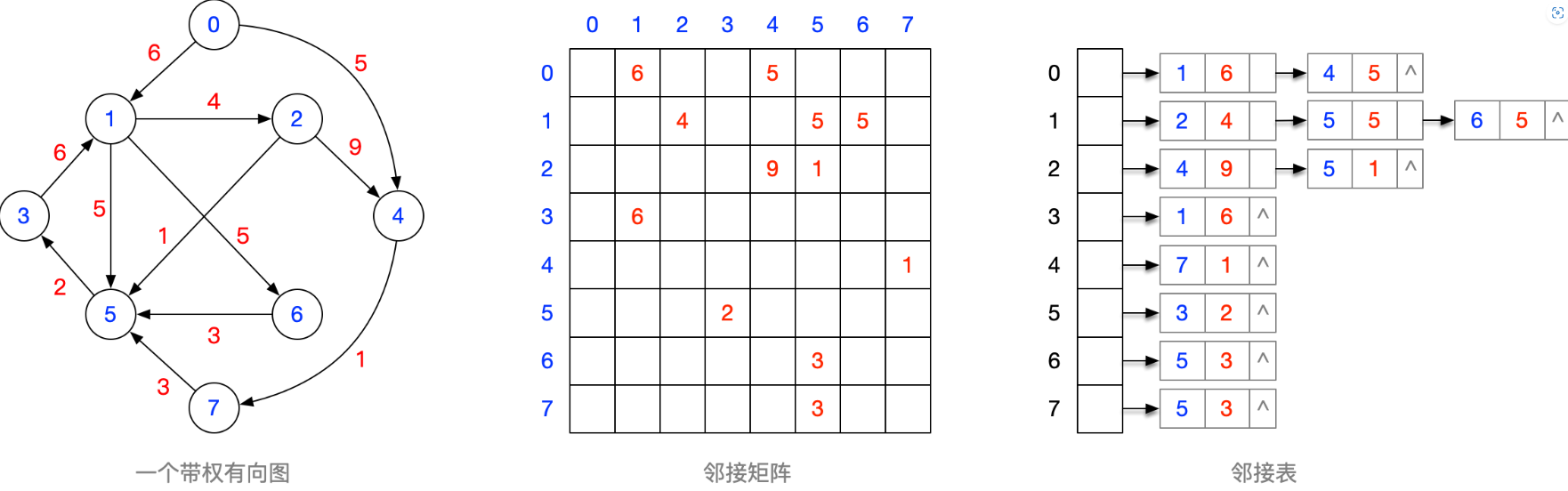
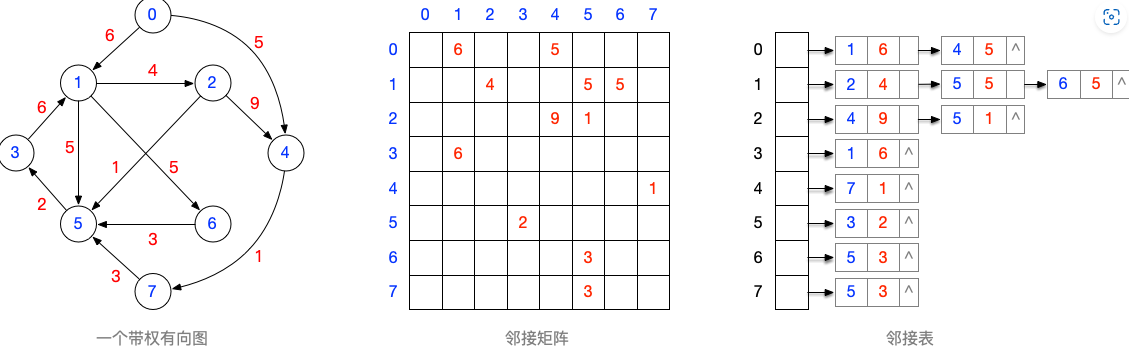
自己设计一个不少于6个结点的带权有向图,并画出其邻接矩阵、邻接表的样子
图的应用:最小生成树
自己设计一个不少于6个结点的带权无向连通图,并画出其邻接矩阵、邻接表的样子
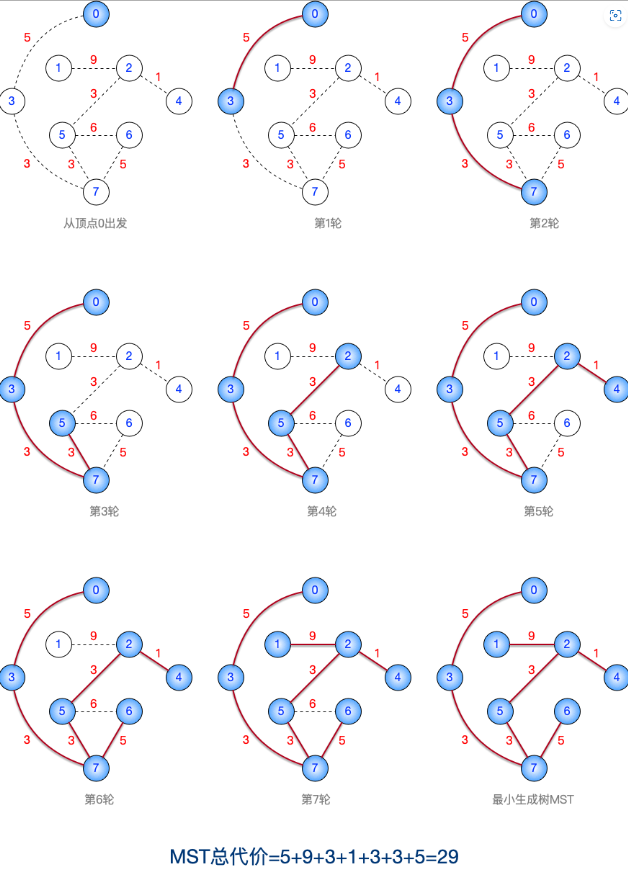
基于上述无向连通图,使用Prim算法生成MST,画出算法执行过程的示意图,并计算MST的总代价
1 | 从顶点0开始,运行 Prim 算法的过程如下: |
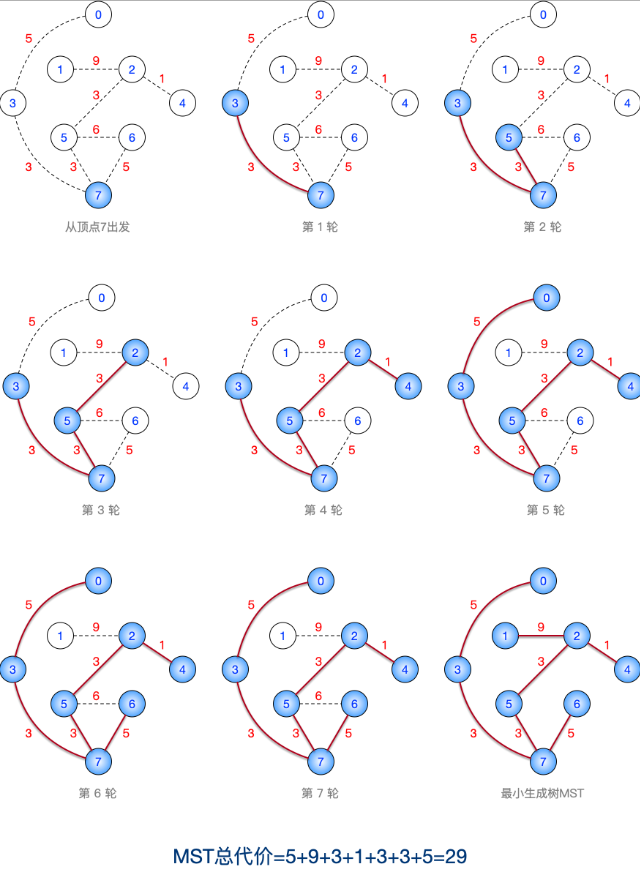
1 | 从顶点7开始,运行 Prim 算法的过程如下。这里想强调的是:当同时有两个代价相同的顶点时,优先将编号小的顶点加入MST。如:第 1 轮从顶点7出发,与其相连的顶点3、顶点5代价都是最小的,优先选择编号更小的顶点3。 |
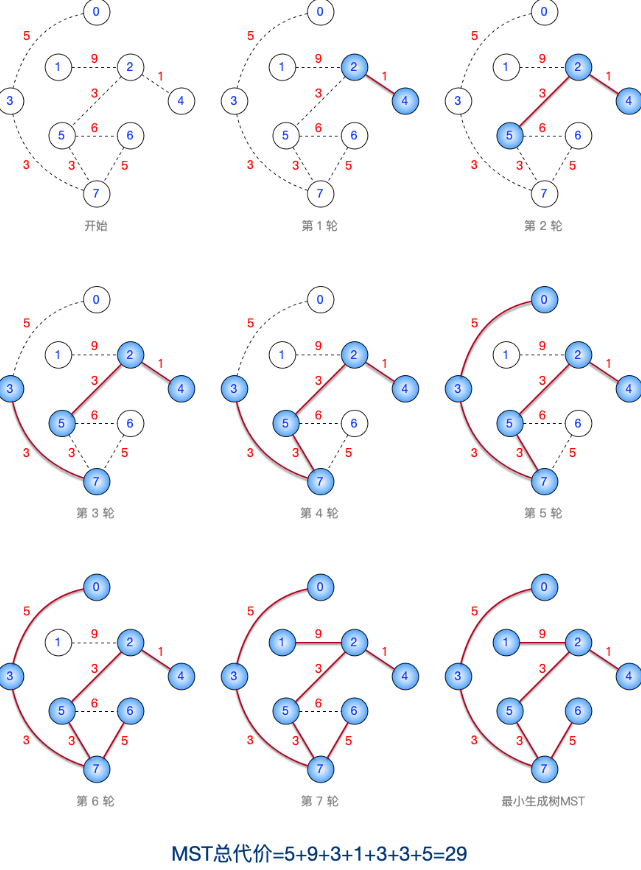
基于上述无向连通图,使用Kruskal算法生成MST,画出算法执行过程的示意图,并计算MST的总代价
1 | Kruskal 算法的执行过程是:先将各条边按照权值递减的排序,再按顺序依次检查是否将这些边加入MST。各条边排序结果如下: |
图的应用:最短路径
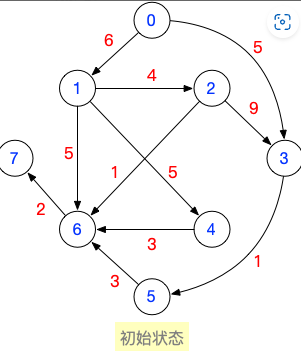
基于你设计的带权有向图,从某一结点出发,执行Dijkstra算法求单源最短路径。用文字描述每一轮执行的过程
下面将从顶点1出发,执行 Dijkstra 算法
注1:如果题目让你描述迪杰斯特拉算法的执行过程,可以试着模仿王道书画一张表。如下所示。你会发现这个表画起来很崩溃,复杂的飞起。相信我,老师改卷也不愿意改这么复杂的答案。因此,考场上不太可能让你画这么复杂的表。
| 顶点(这一列不包含起点) | 第 1 轮 | 第 2 轮 | 第 3 轮 | 第 4 轮 | 第 5 轮 | 第 6 轮 | 第 7 轮 |
| 0 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ |
| 2 | 4 1→2 | 已完成 | 已完成 | 已完成 | 已完成 | 已完成 | 已完成 |
| 3 | ∞ | ∞ | 7 1→5→3 | 7 1→5→3 | 已完成 | 已完成 | 已完成 |
| 4 | ∞ | 13 1→2→4 | 13 1→2→4 | 13 1→2→4 | 13 1→2→4 | 已完成 | 已完成 |
| 5 | 5 1→5 | 5 1→5 | 已完成 | 已完成 | 已完成 | 已完成 | 已完成 |
| 6 | 5 1→6 | 5 1→6 | 5 1→6 | 已完成 | 已完成 | 已完成 | 已完成 |
| 7 | ∞ | ∞ | ∞ | ∞ | ∞ | 14 1→2→4→7 | 已完成 |
| 集合S | {1, 2} | {1,2,5} | {1,2,5,6} | {1,2,5,6,3} | {1,2,5,6,3,4} | {1,2,5,6,3,4,7} | {1,2,5,6,3,4,7,0} |
| 注2:以下是一种更适合考试的“简洁答题方法”。自己打草稿,快速确定每一轮Dijkstra算法的运行结果,然后按下面这种方式答题到试卷上。 |
答:
从顶点1出发,运行迪杰斯特拉算法的过程如下:
第一轮:顶点1到2的最短路径为 1→2,距离为4
第二轮:顶点1到5的最短路径为 1→5,距离为5
第三轮:顶点1到6的最短路径为 1→6,距离为5
第四轮:顶点1到3的最短路径为 1→5→3,距离为7
第五轮:顶点1到4的最短路径为 1→2→4,距离为13
第六轮:顶点1到7的最短路径为 1→2→4→7,距离为14
第七轮:不存在顶点1到0的路径,距离为∞
图的应用:拓扑排序
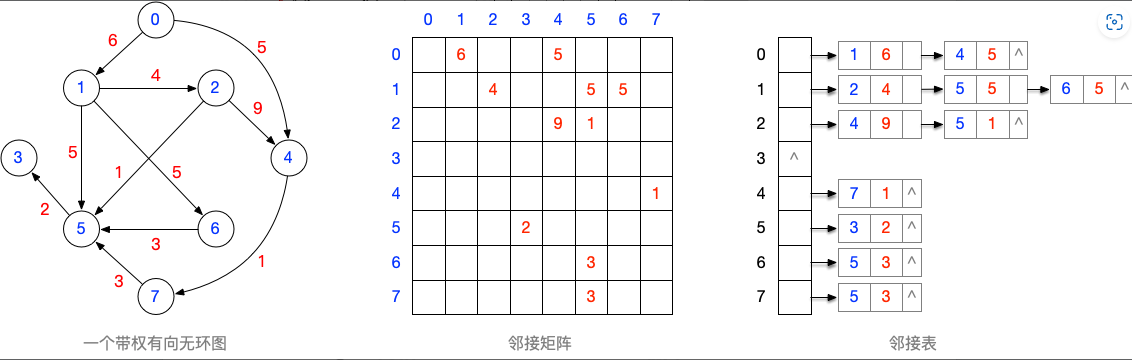
自己设计一个不少于6个结点的带权有向无环图,并画出其邻接矩阵的样子
用一维数组将你设计的有向无环图的邻接矩阵进行压缩存储
注:有向无环图,一定可以转化为一个上三角或下三角矩阵。但是需要调整顶点的编号。
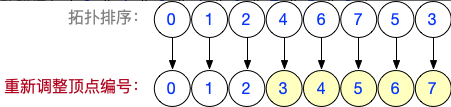
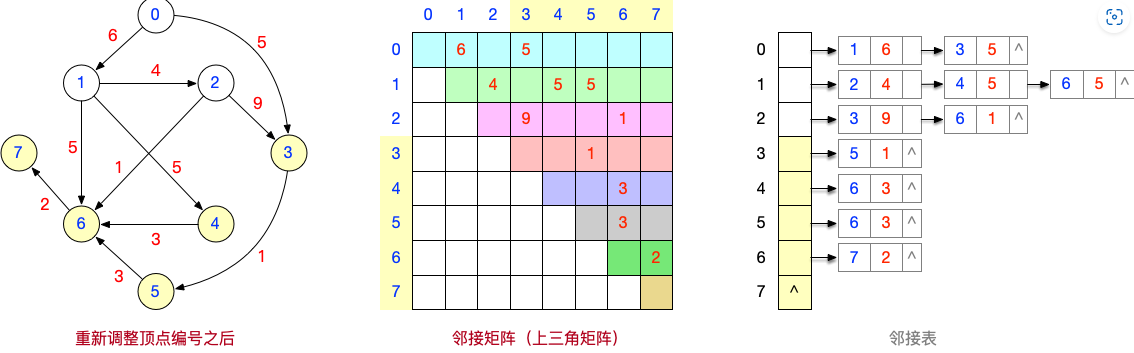
如果要用上三角矩阵表示有向无环图的邻接矩阵,可以对图进行拓扑排序,按照拓扑排序序列,重新调整各个顶点的编号。这样可以确保,所有的弧都是从小编号顶点指向大编号顶点,从而也就保证了邻接矩阵可以转化为“上三角矩阵”
“上三角矩阵”可以按行优先压缩存储,如下所示:
基于你设计的带权有向无环图,写出所有合法的拓扑排序序列
拓扑排序序列1:0,1,2,3,4,5,6,7
拓扑排序序列2:0,1,2,3,5,4,6,7
拓扑排序序列3:0,1,2,4,3,5,6,7
拓扑排序序列4:0,1,4,2,3,5,6,7
文字描述:拓扑排序的过程
图的应用:关键路径
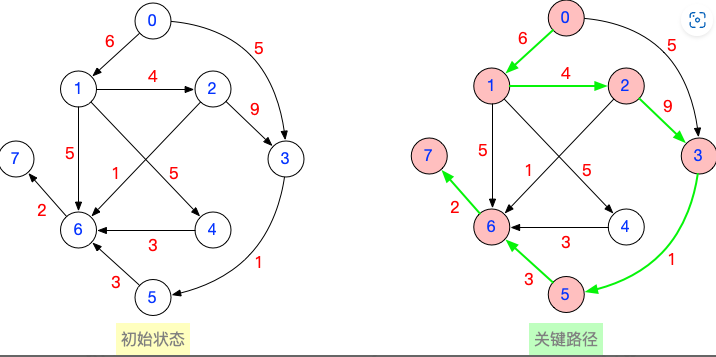
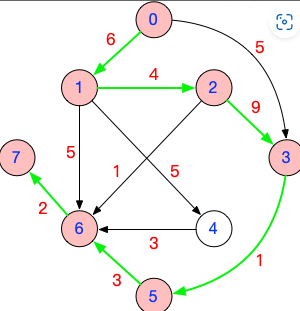
基于你设计的带权有向无环图,写出所有合法的关键路径,并算出关键路径总长度
1 | 用手算的方式求关键路径,就是要找到从起点到终点的所有路径中最长的那条。 |
文字描述:关键路径总长度的现实意义是什么?
AOE网可以表示一个项目,每个顶点表示事件,每个有向边表示活动。关键路径的总长度为25,意味着从启动项目到完成该项目,时间开销至少需要25。
查找算法的分析和应用
考研大纲中,要求我们掌握的查找算法是:
1. 顺序查找
2. 分块查找
3. 折半查找
4. 树形查找(二叉查找树、平衡二叉树、红黑树)
5. B树
6. 散列查找
7. 字符串的模式匹配
其中,顺序查找过于简单,不可能在应用题中专门考察;红黑树、B树难度较大,也不太可能在应用题中专门考察;字符串的模式匹配通常以小题考察为主。因此,在应用题中最有可能专门考察的是 分块查找、折半查找、二叉查找树、平衡二叉树、散列查找。其中,二叉查找树、平衡二叉树的可能考法已在本文档的 3.6 有详细介绍。接下来我们主要训练 分块查找、折半查找、散列查找在应用题中的可能考法
分块查找
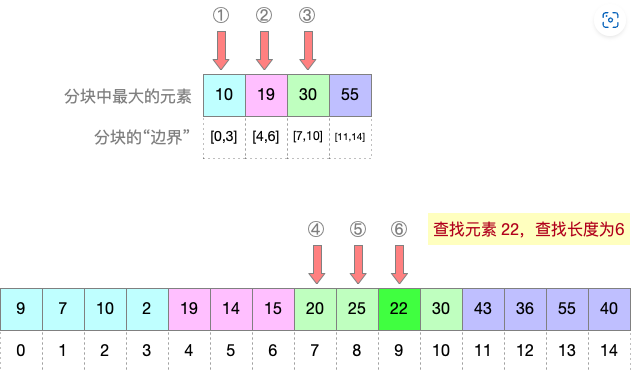
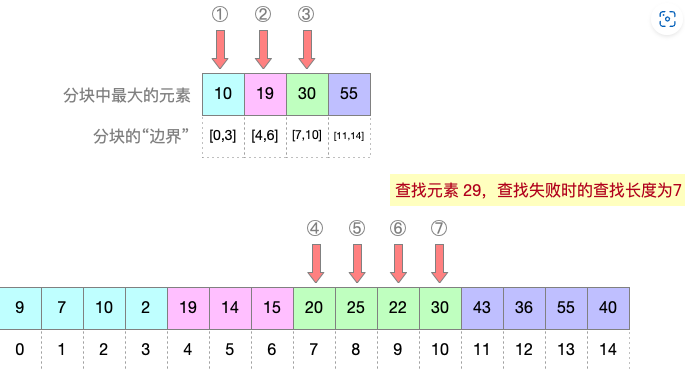
自己设计一个分块查找的例子,不少于15个数据元素,并建立分块查找的索引
基于上述例子,计算查找成功的ASL、查找失败的ASL
上图中,共有15个元素,计算查找成功时的平均查找长度ASL,每个元素被查找的概率相同,都是 1/15。每个元素的查找都需要先查分块索引,再顺序查找分块内各个元素。
查找元素9时,查找长度为 1+1
查找元素7时,查找长度为 1+2
查找元素10时,查找长度为 1+3
查找元素2时,查找长度为 1+4
查找元素19时,查找长度为 2+1
查找元素14时,查找长度为 2+2
查找元素15时,查找长度为 2+3
查找元素20时,查找长度为 3+1
查找元素25时,查找长度为 3+2
查找元素22时,查找长度为 3+3
查找元素30时,查找长度为 3+4
查找元素43时,查找长度为 4+1
查找元素36时,查找长度为 4+2
查找元素55时,查找长度为 4+3
查找元素40时,查找长度为 4+4
综上,查找成功的ASL=(2+3+4+5+3+4+5+4+5+6+7+5+6+7+8)×1/15=4.933
对于查找失败的情况,题目不太可能让你分析查找失败的平均查找长度ASL(因为查找失败的情形很多,我们无法预估出现每一种失败情形的概率)。
因此,如果分块查找要考察“查找失败”的情形,很有可能是给你一个特定的关键字,让你分析该关键字查找失败时的查找长度。
例:如下图所示,查找元素 29(查找失败)时,首先顺序查找分块索引;确认元素29属于第三个分块,该分块在数组中下标范围是 7-10;紧接着在数组中查找下标为 7-10 的几个元素,所有元素和目标关键字都不匹配,最终可确定查找失败。
综上,查找元素 29(查找失败)时,总计对比关键字7次。
折半查找
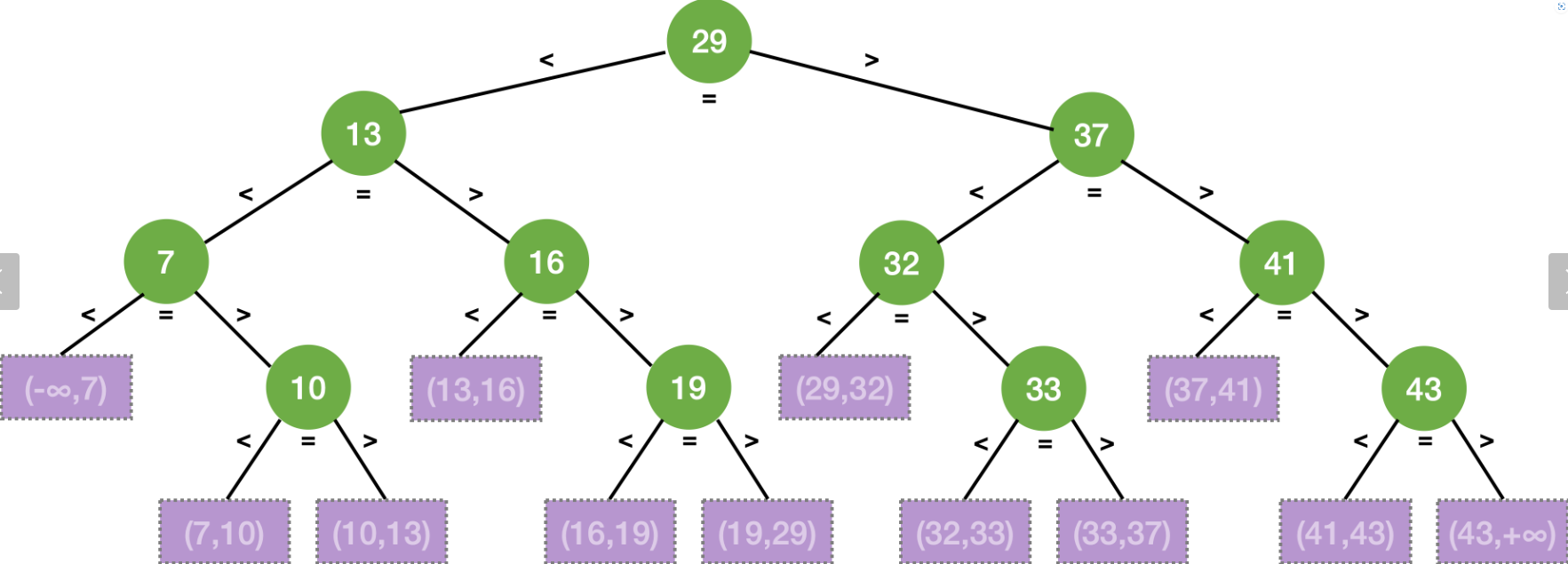
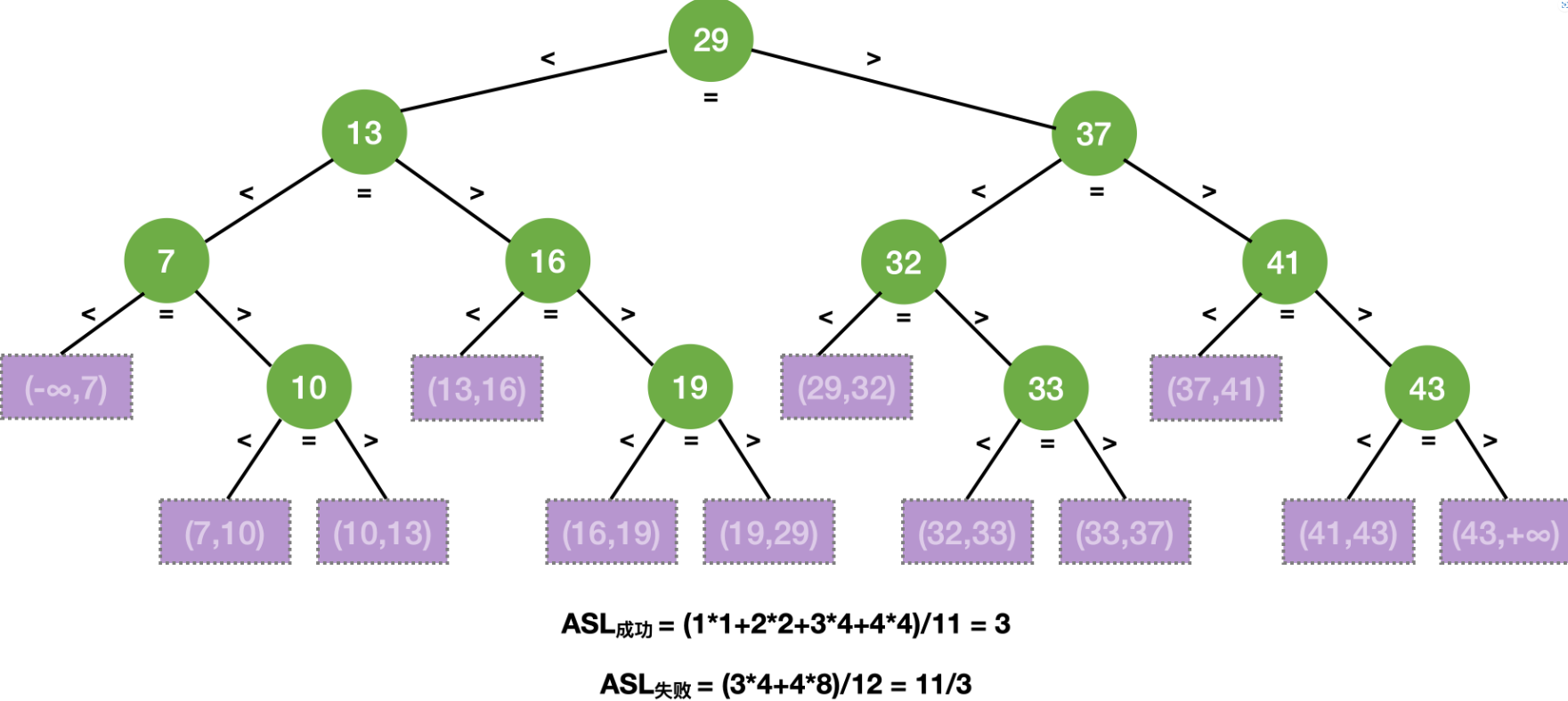
自己设计一个折半查找的例子,不少于10个数据元素,画出对应的查找分析树
基于上述例子,计算查找成功的ASL、查找失败的ASL
散列查找
自己设计一个散列表,总长度由你决定,并设计一个合理的散列函数,使用线性探测法解决冲突
设散列表长度为16,采用线性探测法解决冲突,从空表开始,依次插入关键字 {19, 14, 23, 1, 68, 20, 84, 27, 55, 11, 10, 79},散列函数 H(key)=key%13
注:散列表的长度可以比散列函数的映射范围更大,散列函数的映射范围是 0-12,散列表的后面几个位置 13-15 不可能被散列函数直接映射,但是在线性探测法处理冲突时,可能被使用到
基于上述例子,计算查找成功的ASL、查找失败ASL
考虑查找成功的所有情况。各元素查找成功时的查找长度如下:
考虑查找失败的所有情况。若目标元素的散列值为0,则只需对比位置0的关键字即可确定查找失败,查找长度为1;若目标元素的散列值为1,采用线性探测法,需对比位置#1-#13,才能确定查找失败,查找长度是13;若目标元素的散列值为2,采用线性探测法,需对比位置#2-#13,才能确定查找失败,查找长度是12;其他散列值同理。
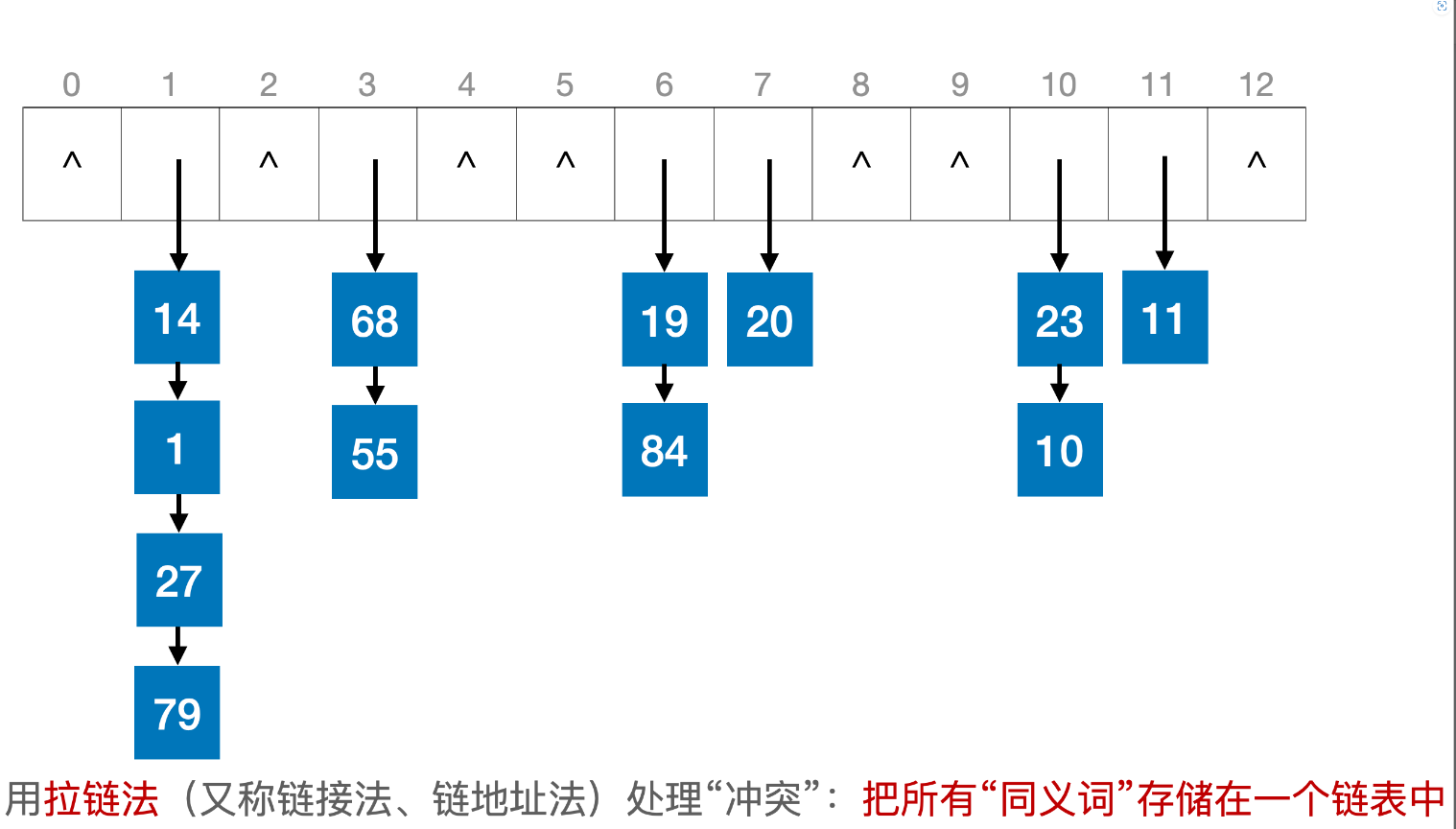
基于上述散列表,设计不少于10个元素的插入序列,依次插入散列表,画出散列表最终的样子(插入过程至少发生4次冲突)
基于上述例子,计算查找成功的ASL、查找失败的ASL
考虑查找成功的所有情况。元素 14、68、19、29、23、11 的查找长度为1;元素1、55、84、10 的查找长度为2;元素27的查找长度为3;元素79的查找长度为4,因此:
考虑查找失败的所有情况。若目标元素的散列值为0,则无需对比任何关键字即可确定查找失败,查找长度为0;若目标元素的散列值为1,则需要依次对比关键字14、1、27、79才能确定查找失败,查找长度为4;其他散列值同理。
排序算法的分析和应用
希尔排序
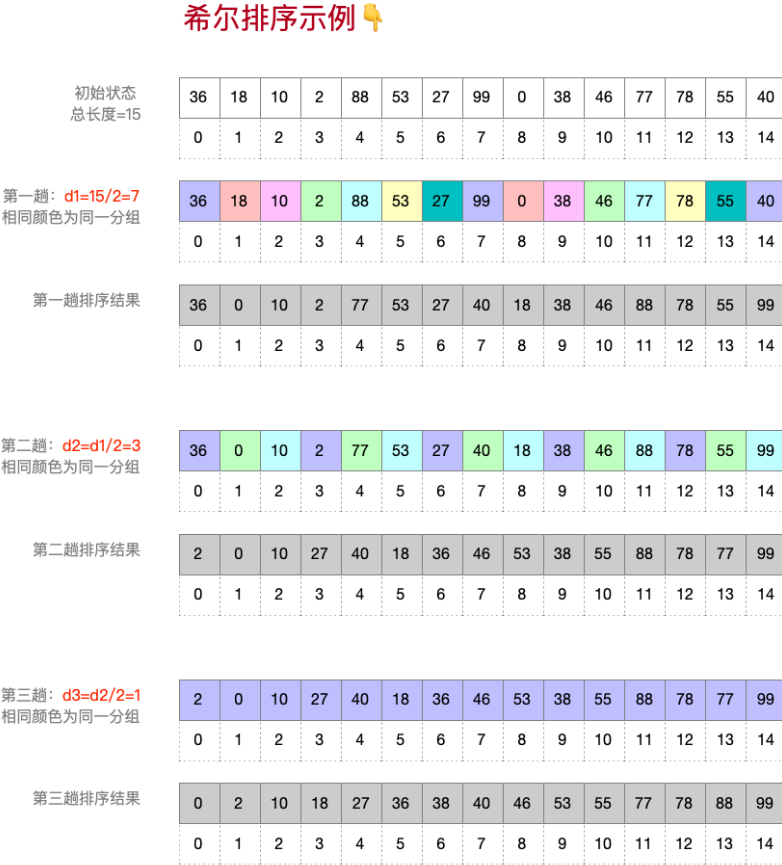
自己设计一个长度不小于10的乱序数组,用希尔排序,自己设定希尔排序参数画出每一轮希尔排序的状态
堆排序
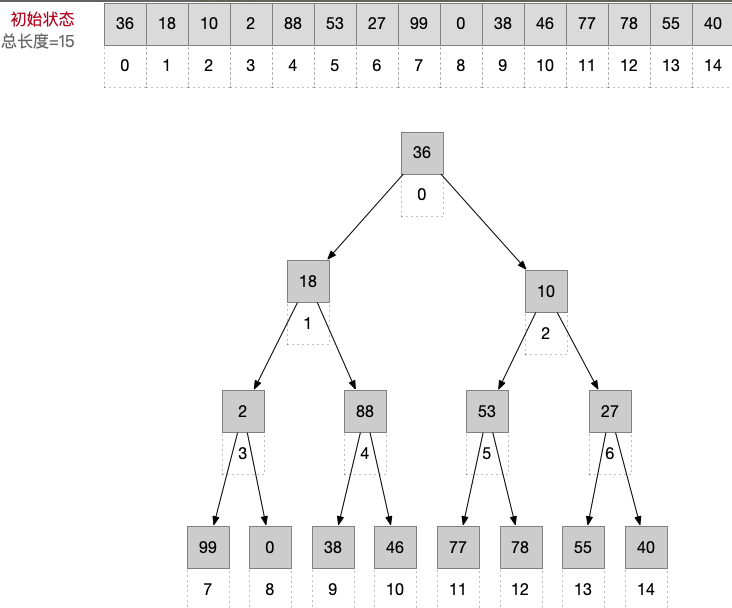
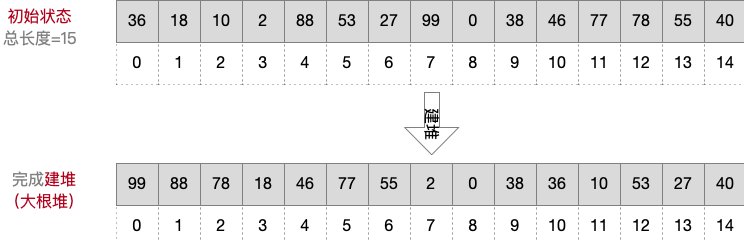
自己设计一个长度不小于10的乱序数组,用堆排序,最终要生成升序数组,画出建堆后的状态
假设乱序数组的初始状态如下,元素从0开始存储👇:
若顺序二叉树从数组下标1开始存储结点,则:
● 结点 i 的父结点编号为i/2
● 结点 i 的左孩子编号为i*2
● 结点 i 的右孩子编号为i*2+1
若顺序二叉树从数组下标0开始存储结点,则:
● 结点 i 的父结点编号为[(i+1)/2] - 1
● 结点 i 的左孩子编号为[(i+1)*2] - 1 = 2*i + 1
● 结点 i 的右孩子编号为[(i+1)*2+1] - 1 = 2*i + 2
在本例中,元素从数组下标0开始存储,因此,0号元素是根节点,1号元素是其左孩子,2号元素是其右孩子。其他元素间的关系如下:
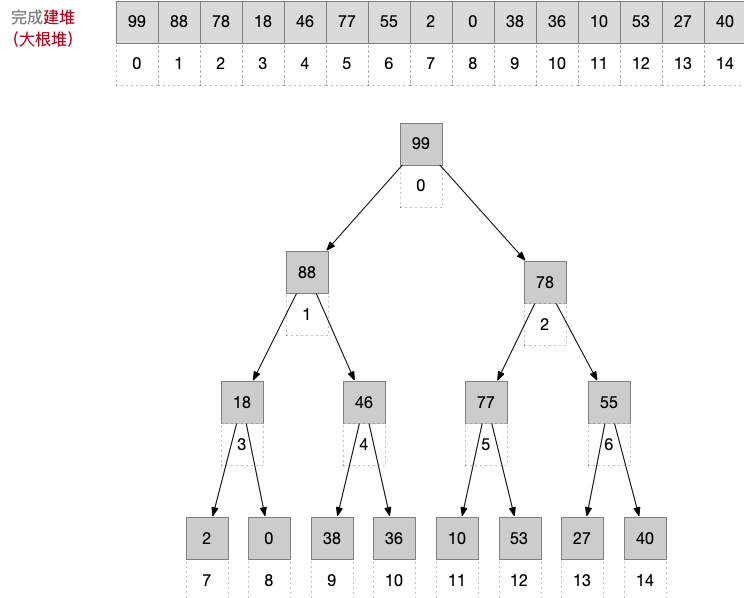
由于最终要生成升序数组,因此需要建立大根堆,从最后一个分支(即6号结点)开始调整,即依次调整结点 6、5、4、3、2、1、0。建立好的大根堆如下:
注:如果应用题让你画出一个乱序数组建堆后的样子,只需要画出数组形式的图示即可,不用画二叉树形态的图示。如下👇
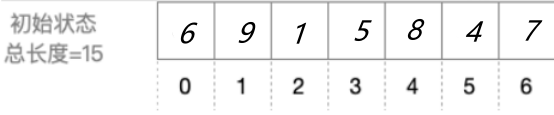
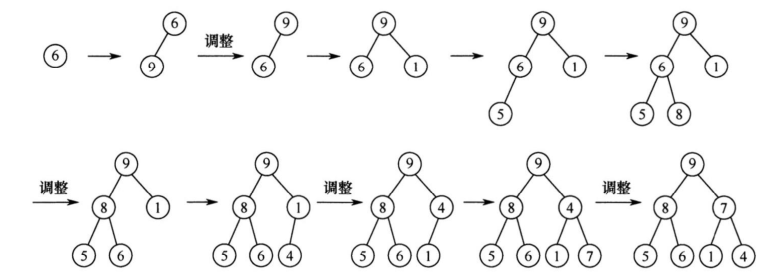
给定一组无序的数,需要依次加入大根堆,给出建立大根堆完整过程
假设乱序数组的初始状态如下,元素从0开始存储👇:
完整建立大根堆过程👇:
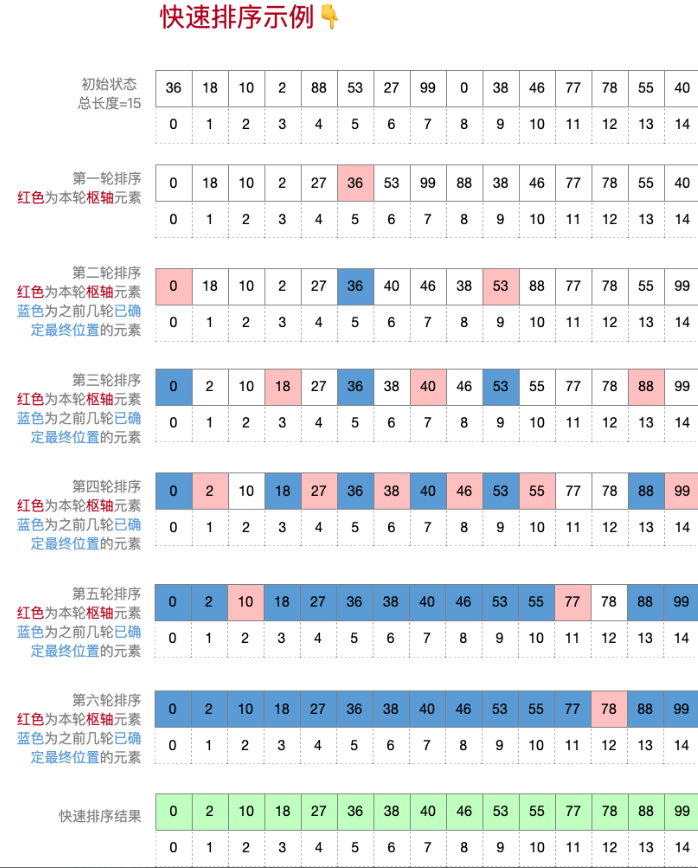
快速排序
自己设计一个长度不小于10的乱序数组,用快速排序,最终要生成升序数组画出每一轮快速排序的状态
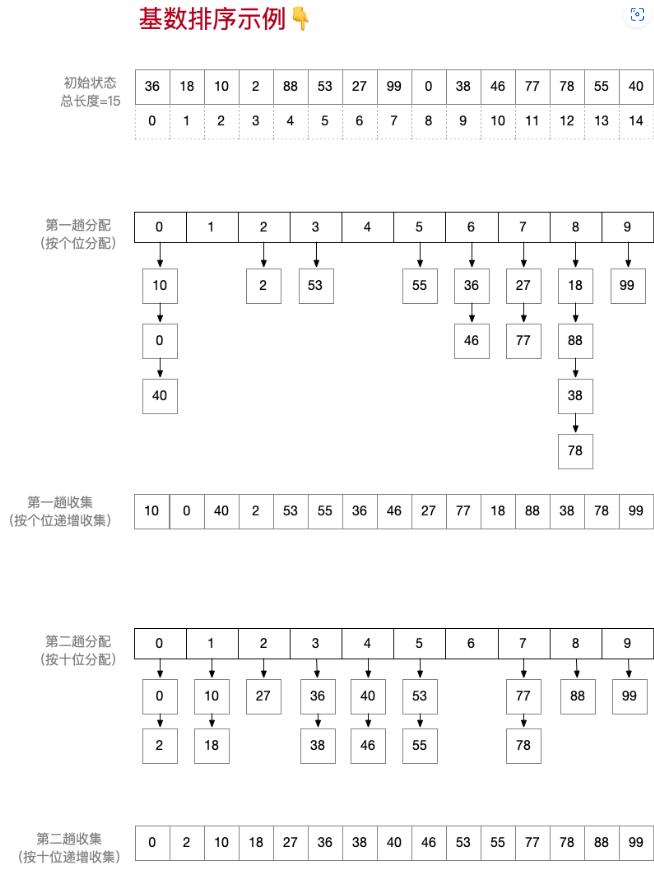
基数排序
自己设计一个长度不小于15的乱序链表,每个数据元素取值范围0~99,用基数排序,最终要生成升序链,画出每一轮基数排序的状态表
外部排序
选择-置换算法
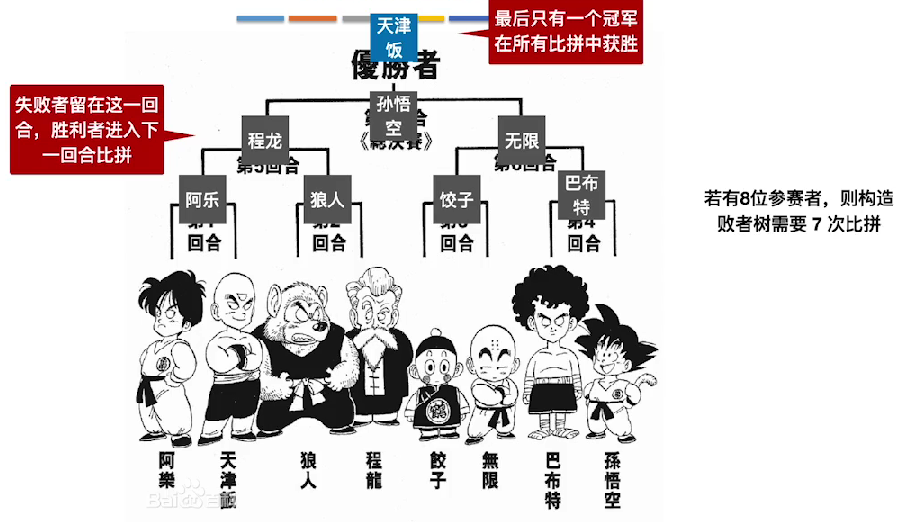
败者树
败者树可以
保留比较的结果记录,使得挑选出最小元素后,新增一个元素进入时,再次挑选最小时,可以根据之前比较的结果,减少比较的次数
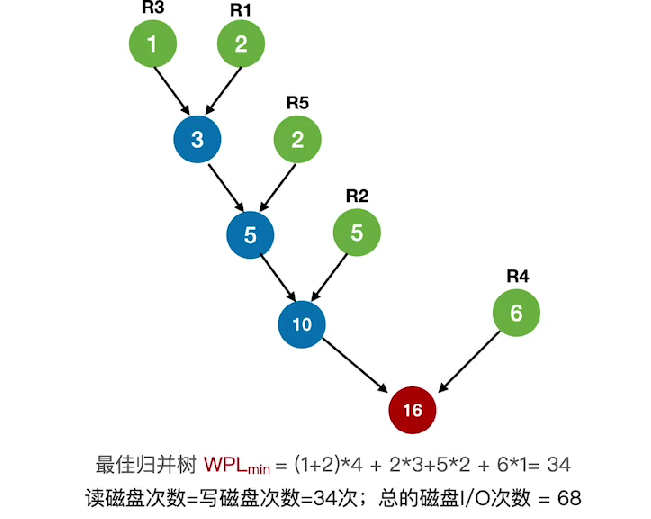
最佳归并树
归并段,使得比较次数最少->归并段的比较构造成哈夫曼树->每次都选择最小的段归并->这就是最佳归并树(比较次数最少即IO磁盘次数最少)
真题训练-应用题
5.5.3-2
答案👇
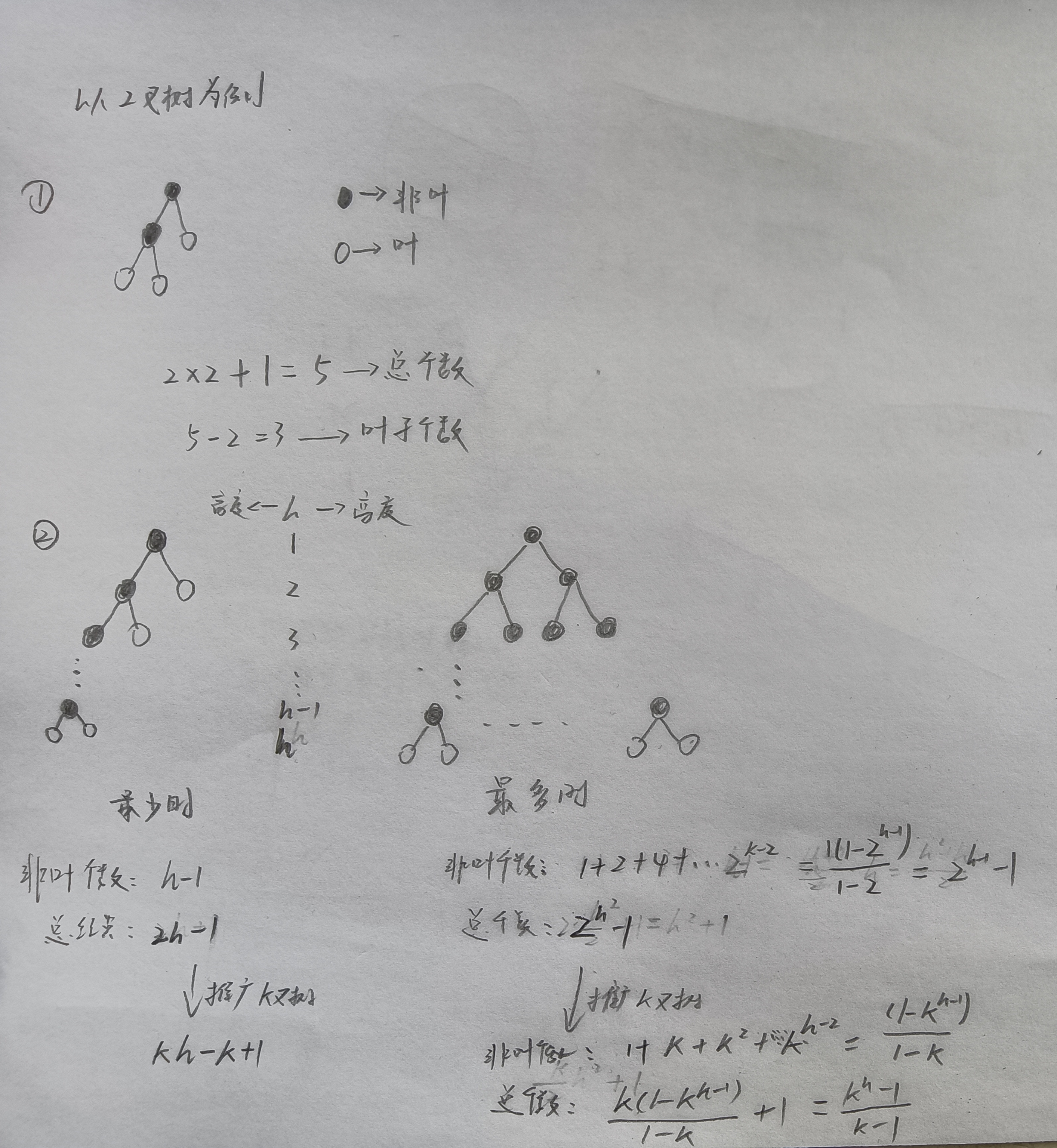
5.4.4-7
答案👇
总结点:km+1
叶结点:km+1-m = (k-1)m + 1
.6.4.6-8
答案👇
6.4.6-9
答案👇
6.4.6-10
答案👇
答案不唯一,但是分析思路相通
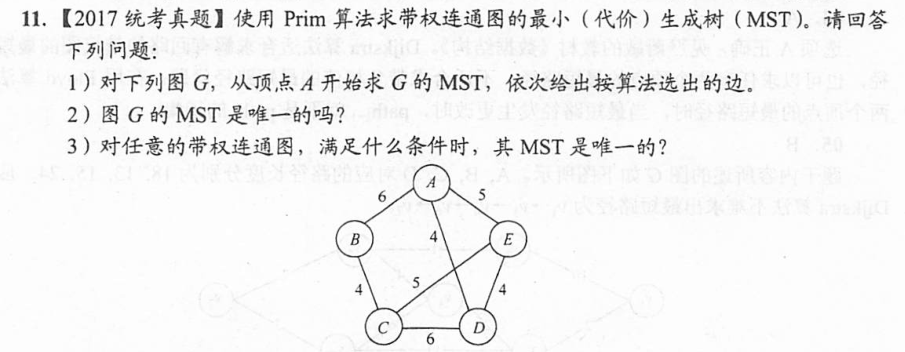
6.4.6-11
答案👇
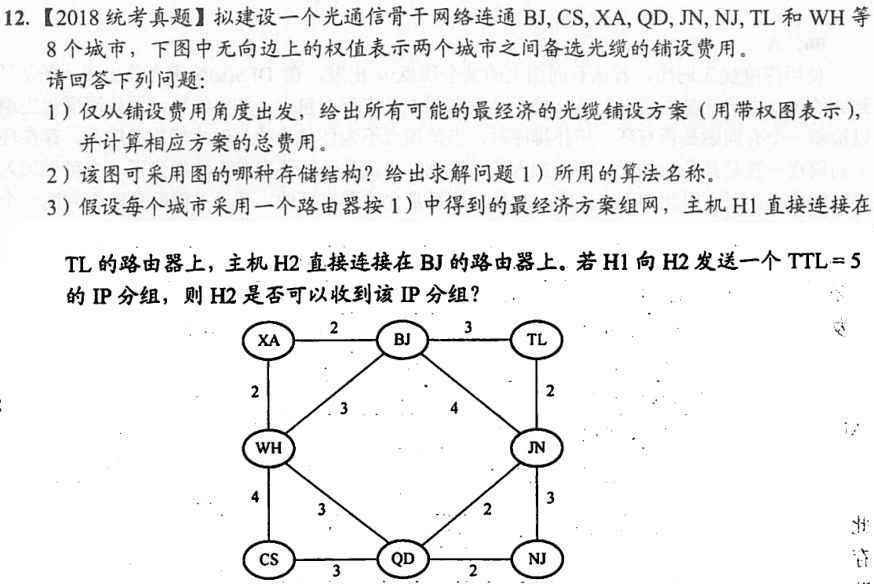
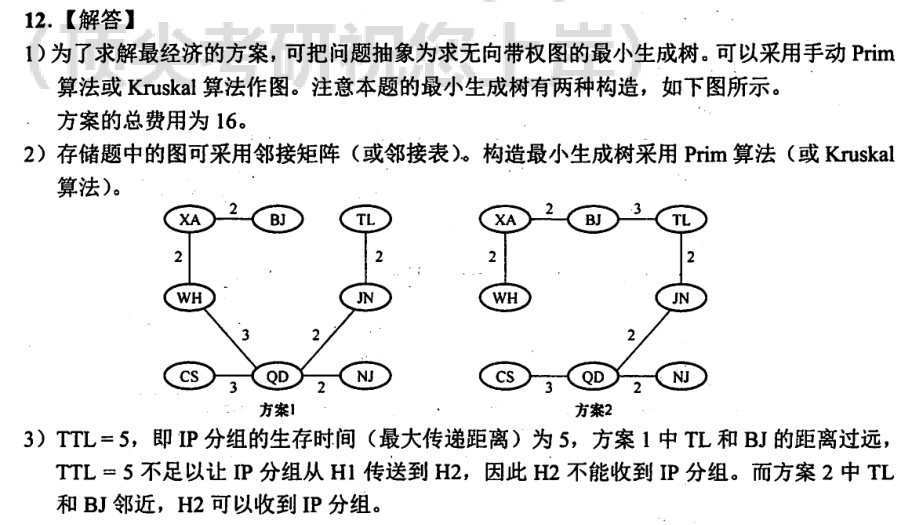
6.4.6-12
答案👇
2020-42
答案👇
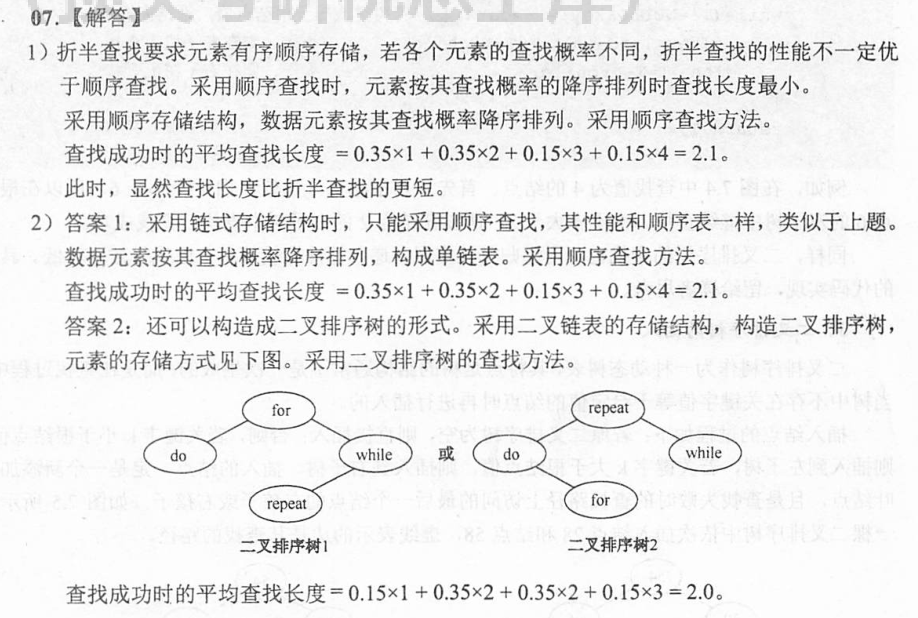
7.2.4-7
答案👇
7.5.5-6
答案👇
装填因子: a=n/m 其中n 为关键字个数,m为表长。散列函数的含义- 散列存储冲突解决方法之一–
线性探测法:冲突,往后跳一格
3.2.5-4
答案👇
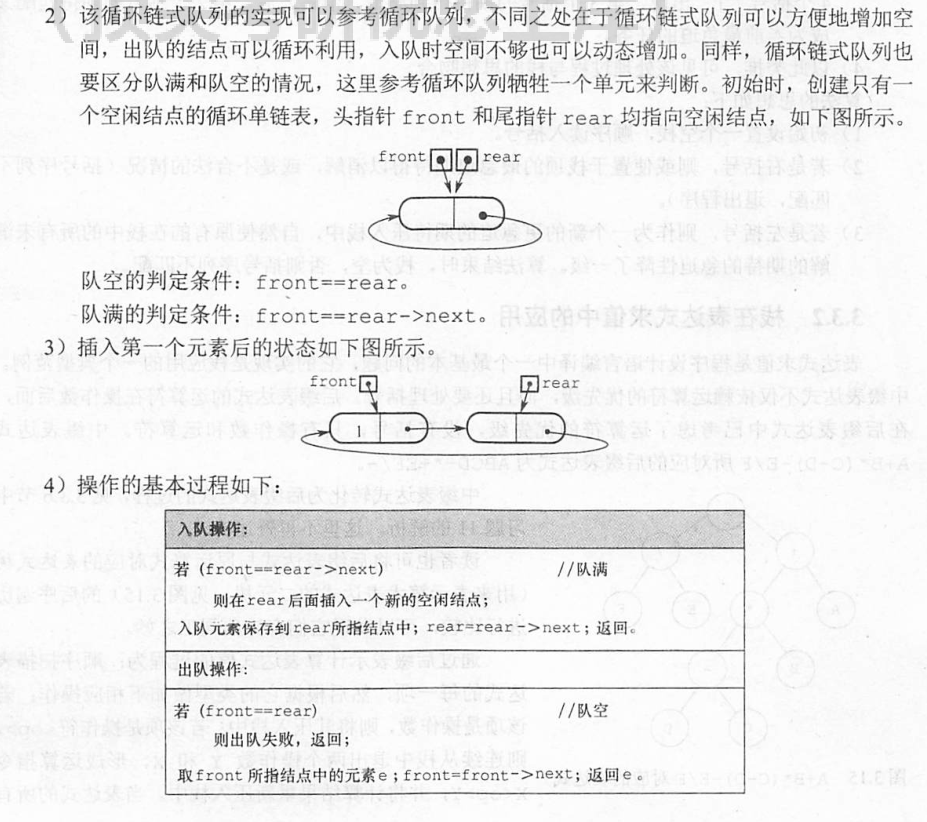
- 选择链式存储,采用循环链表
- 队空,rear==front;队满,rear->next=front;
2023-42
答案👇
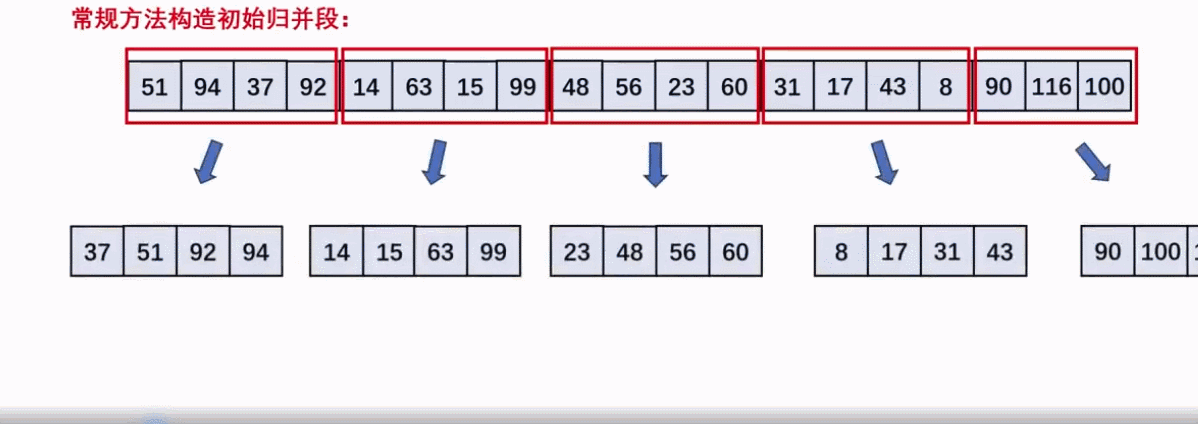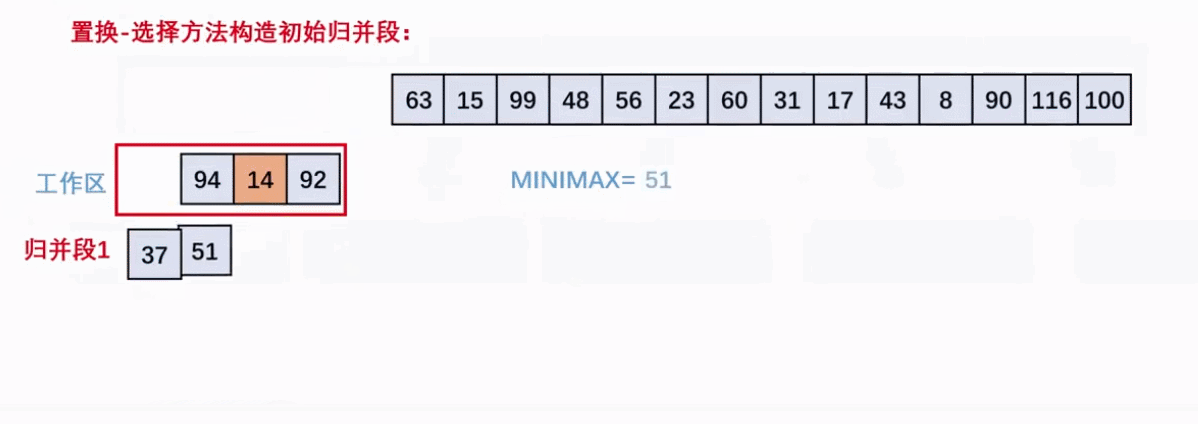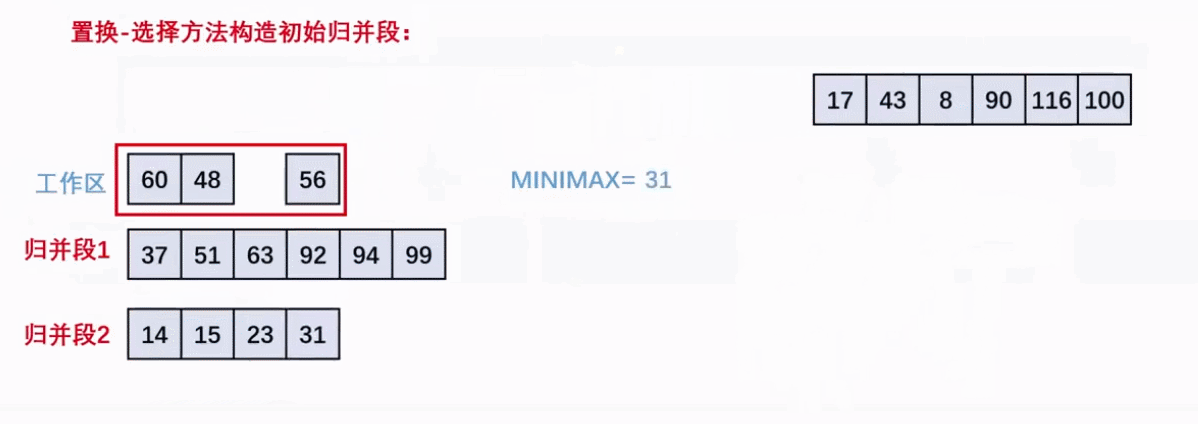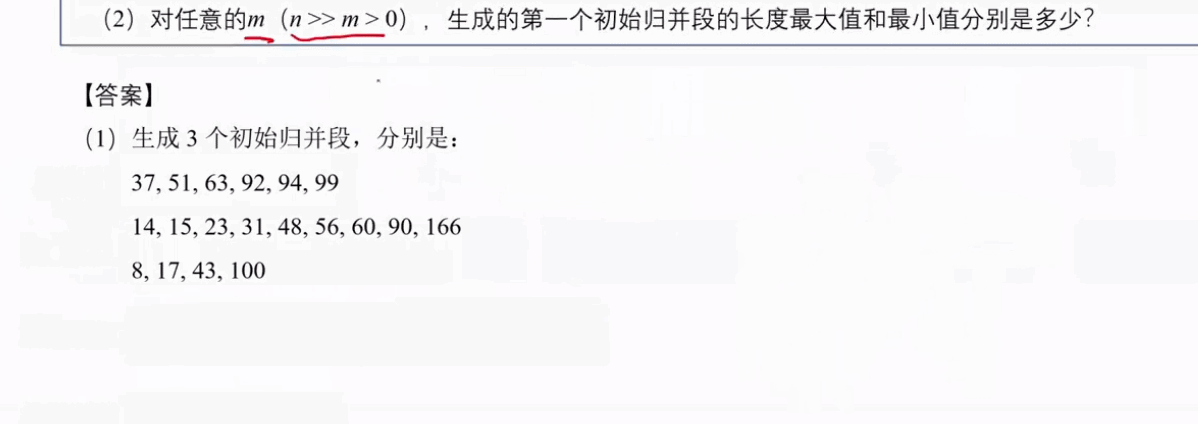
外部排序——置换-选择排序生成初始归并段
- 按照工作区大小m将n个数据分为n/m组
- 工作区初始填装第一组数据,并选择其中最小的加入归并段并设置
minMax=当前加入的数据 - 然后依次往右扫描用剩余的填补空缺的工作区,再次从中选择
大于minMax的最小数据加入归并段。 - 重复2,3.直至工作区
均小于minMax
真题训练-算法题
算法题型
- 顺序表、链表
- 树和二叉树
- 图
- 查找
- 排序
算法专项总结
- 不要过度追求最优解,除了树/图只有一种解
- 掌握快速排序(背诵)
- 空间换时间——辅助数组
- 双指针(快满指针)
- 树——掌握遍历
- 图——掌握存储结构
- 查找——折半查找
- 排序——快排、归并
常用的快速排序代码
假如每次快速排序数组都被平均地一分为二,那么可以得出QuickSort递归的次数是Iog2n,第一次partition遍历次数为n,分成两个数组后,每个数组遍历n/2次,加起来还是n,因此
时间复杂度是O(nlog2n);快排的
空间复杂度是O(log2n),因为递归的次数是log2n,而每次递归的形参都是需要占用栈空间的。
1 | int partition(int A[],int low,int high){ //一趟划分 |
顺序表
2010-42
1 |
|
2013-41
1 | //思想,申请一个数组B,记录遍历数组A时,不同数据的出现次数。同时一边记录一边检查次数是否超过n/2。时间复杂度O(n),空间复杂度(n) |
链表
预测
1 | typedef struct LNode{ |
树和二叉树
强化试卷-2
答案👇
1)算法思想:
由题⽬已知⼆叉树⾼度为H,因此可设置⽤于统计的数组 width[H],其中,width[i] 表示第 i 层共有⼏个结点(不妨规定层数从0开始);
使⽤⼆叉前序遍历的思想,遍历的同时,判断结点所处层数 i,令 width[i]++;
遍历完所有结点后,找到 width 数组中最⼤的值,即为⼆叉树的宽度。
1 | void PreOrder(int width[],int deep,BiTree T){ |
预测–层次遍历
1 |
|
预测
1 | //day23解析,难度:适中 |
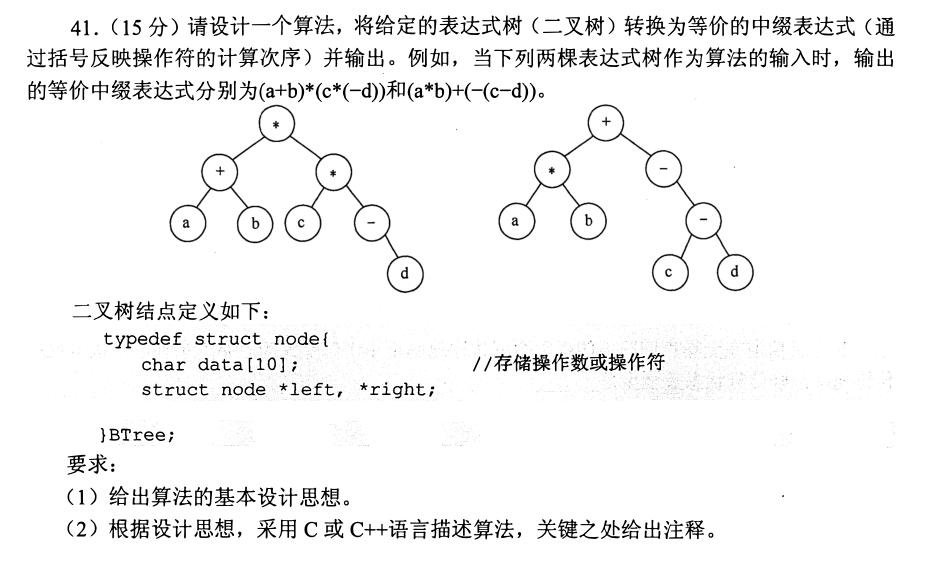
2017
1 | //设计思想:中序遍历序列就是中序表达式序列;括号碰到非根节点和叶子结点需要添加括号 |
2014
1 | //递归实现,从根节点开始,深度优先遍历(先序遍历),设置一个int变量记录深度,遍历到叶子结点时,WPL+=deep*weight |
查找
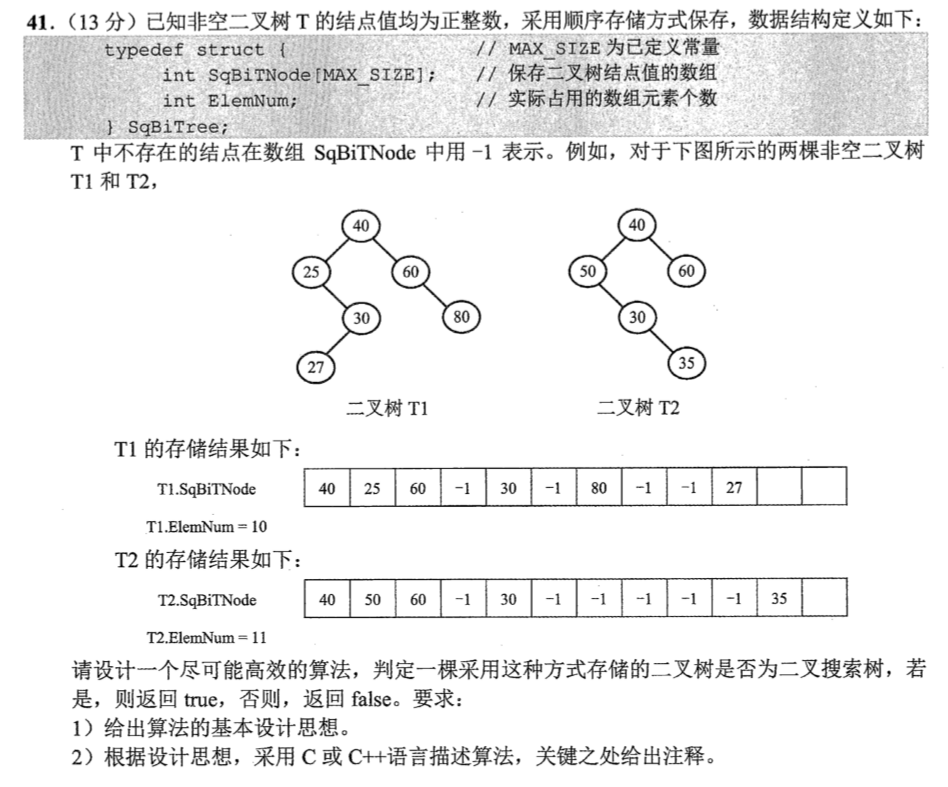
2022
1 | //(1).顺序存储的二叉树,下标k的左右子树下标分别为2k+1 ,2k+2;根据二叉排序树的性质,中序遍历后,其遍历结果是升序,所以可以对树进行递归的中序遍历,将遍历结果用数组存储,然后对数组进行遍历看是否是升序。 |
图
2021
1 | int Is ExistEL(MGraph G){ |
2023
1 | int printVertices(MGraph G){ |
排序
2016
1 | //先排序,后从中间划分 |
考点
- 时间复杂度与空间复杂度
- 线性表的顺序存储
- 线性表的链式存储
- 栈和队列的基本性质
- 栈和队列的存储结构
- 双端队列
- 栈和队列的应用
- 特殊矩阵的压缩存储+多为数组存储
- 串的模式匹配算法
- 树的基本性质
- 二叉树的定义与性质
- 二叉树的遍历
- 树森林二叉树的转换
- 线索二叉树的基本概念和构造
- 哈夫曼树和哈夫曼编码
- 并查集
- 图的基本概念
- 图的存储结构与基本操作
- 图的遍历
- 最小生成树
- 最短路径
- 拓扑排序
- 关键路劲
- 有向无环图存储算数表达式
- 顺序查找、折半查找
- 二叉排序树
- 二叉平衡树
- 红黑树
- B树和B+树
- 散列表
- 插入排序
- 交换排序
- 选择排序
- 二路归并排序
- 基数排序
- 各种内部排序算法的比较
- 外部排序思想