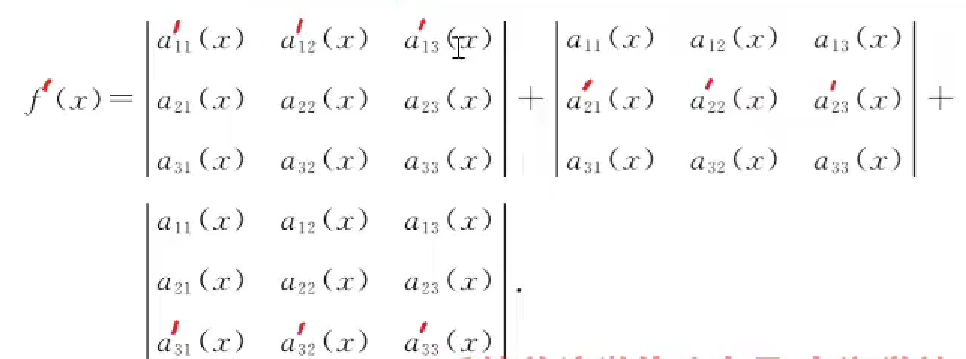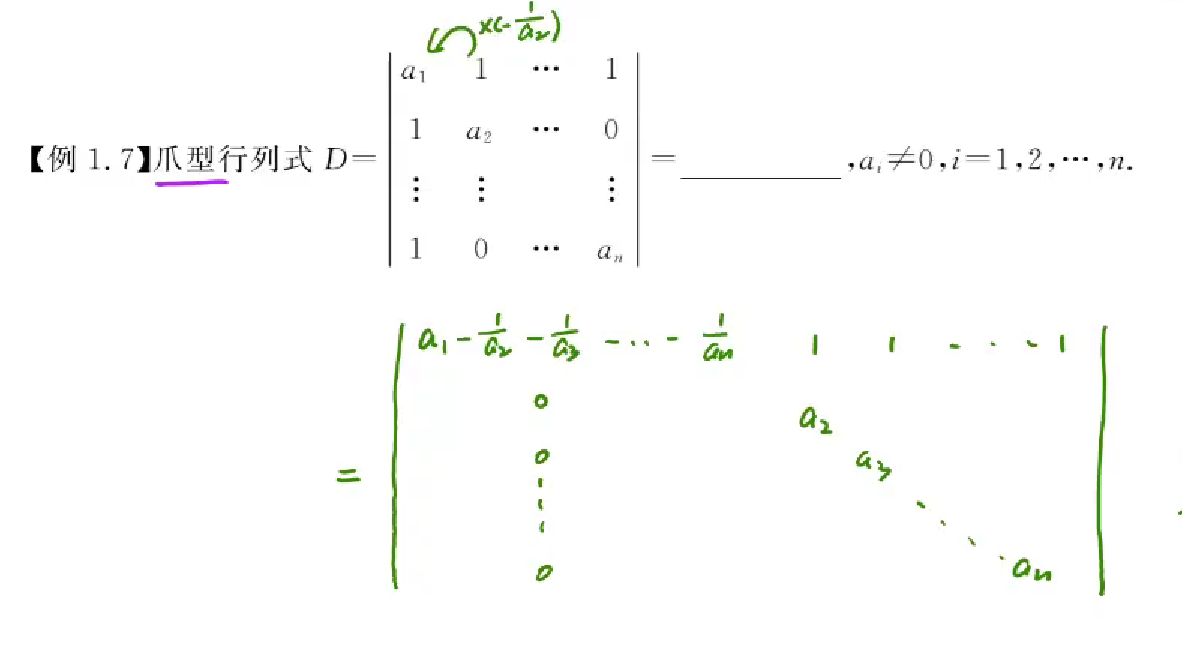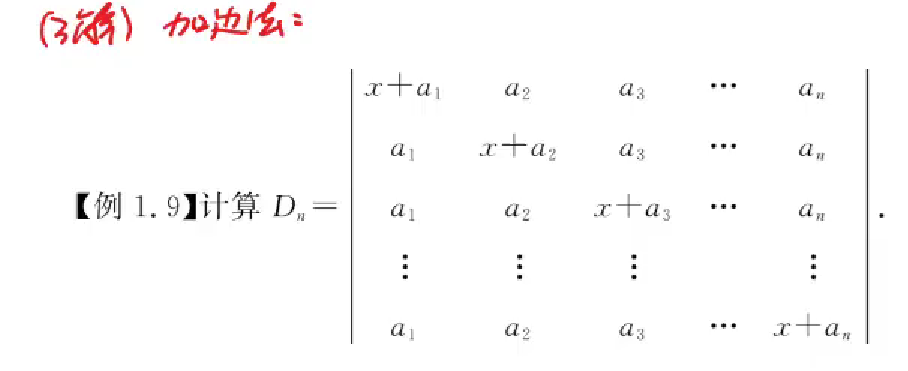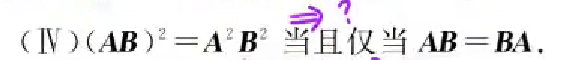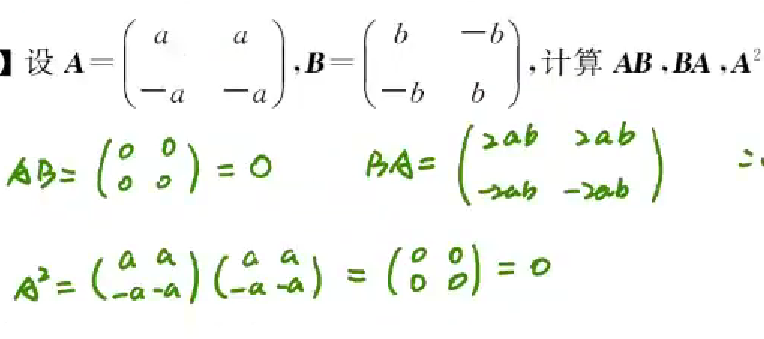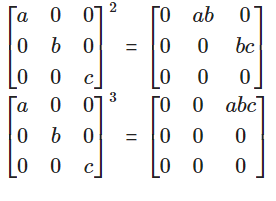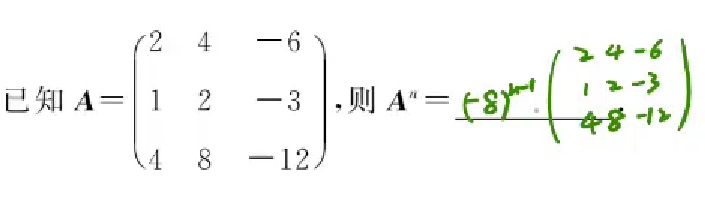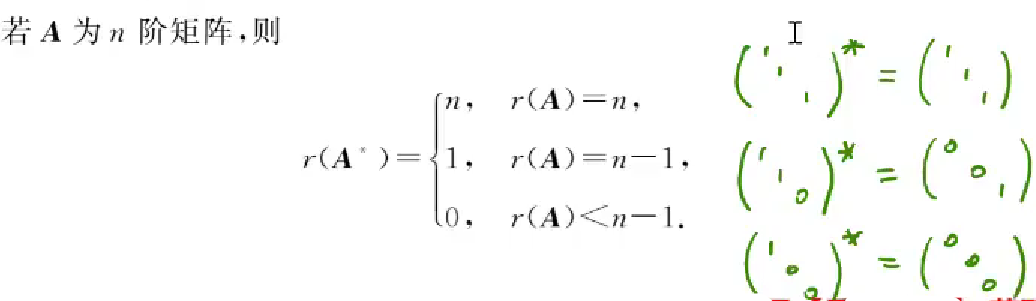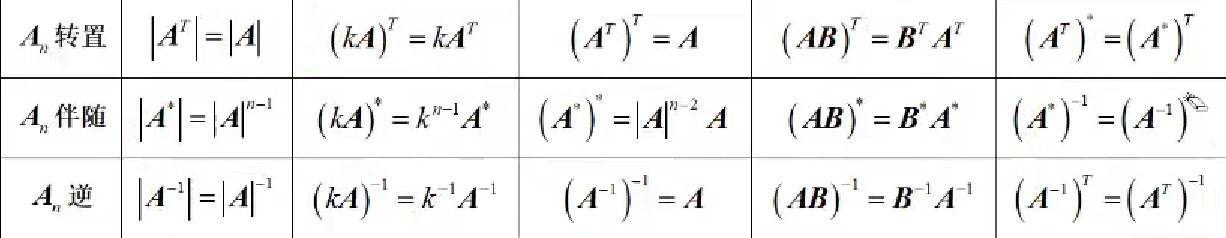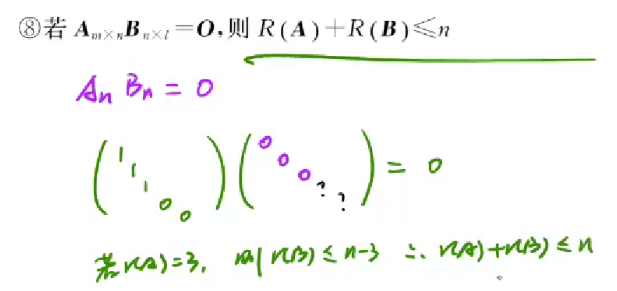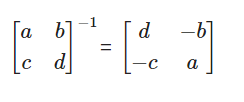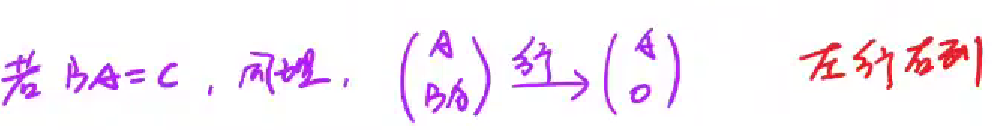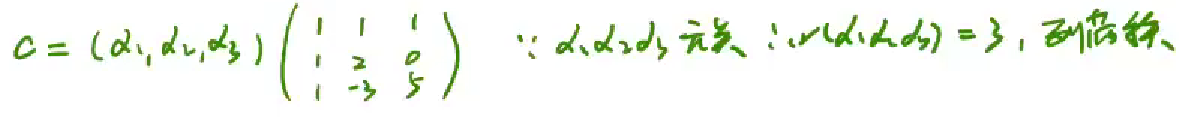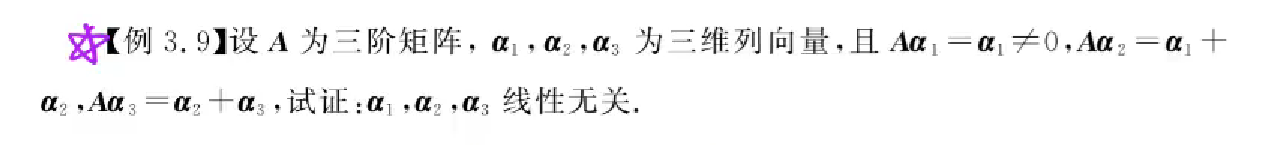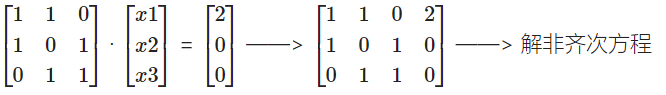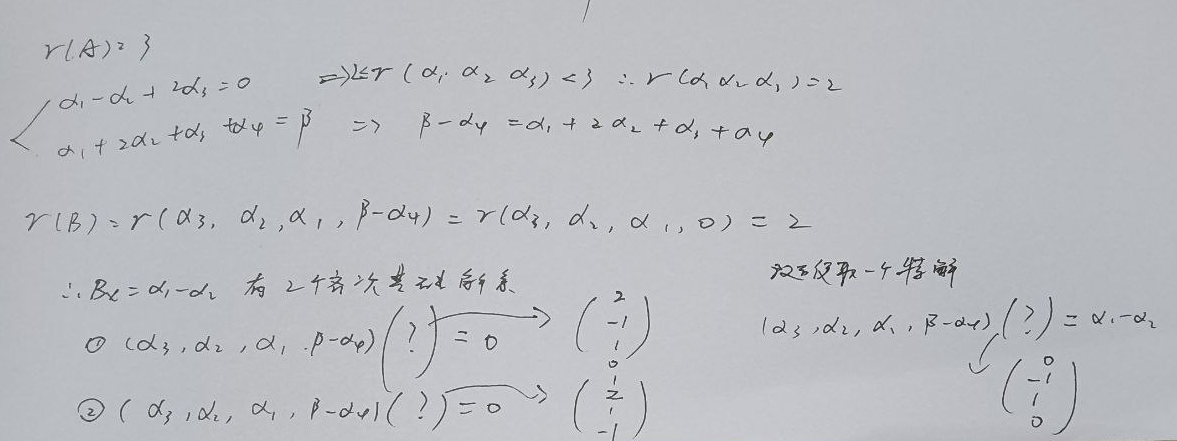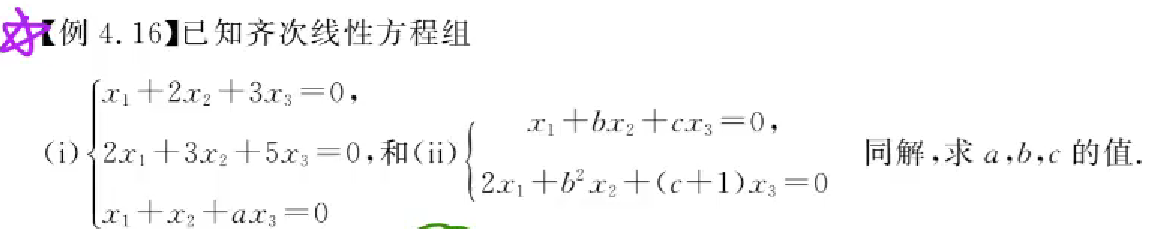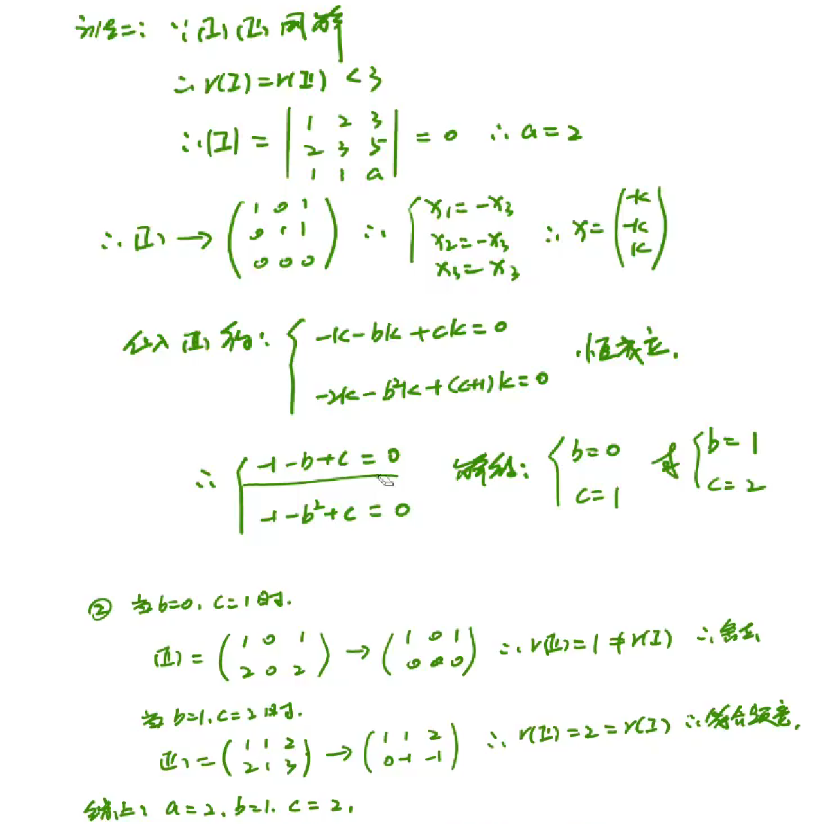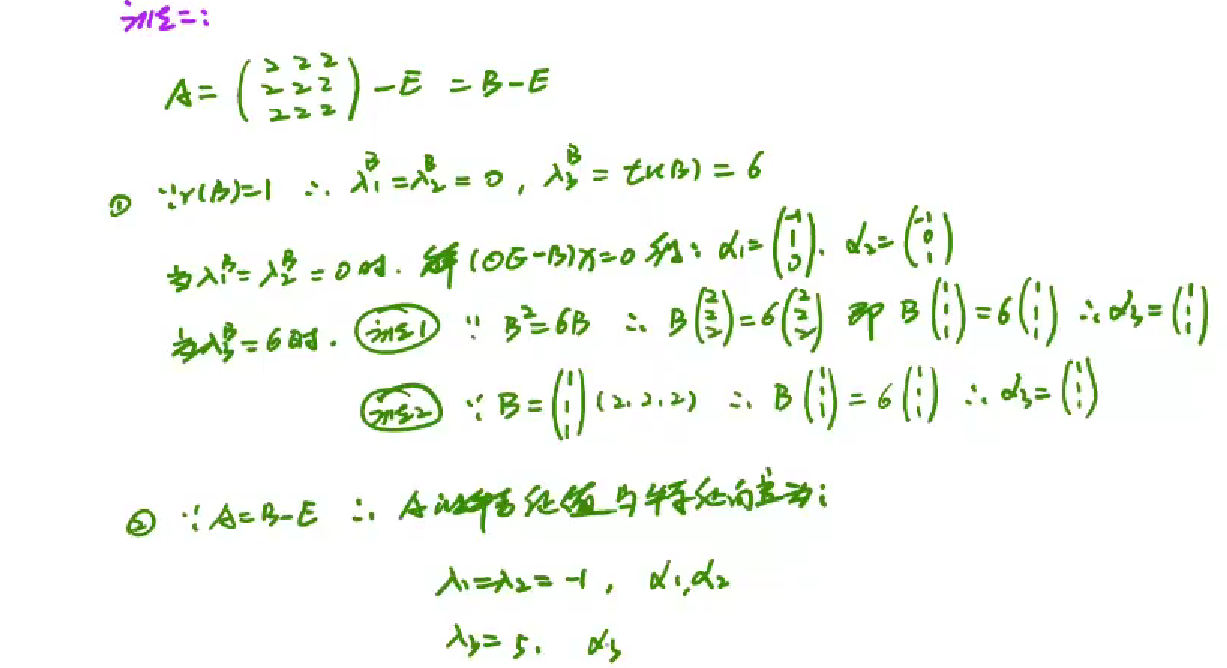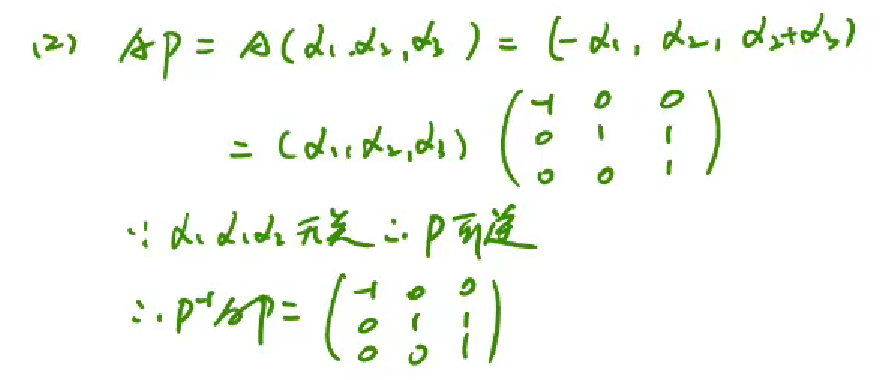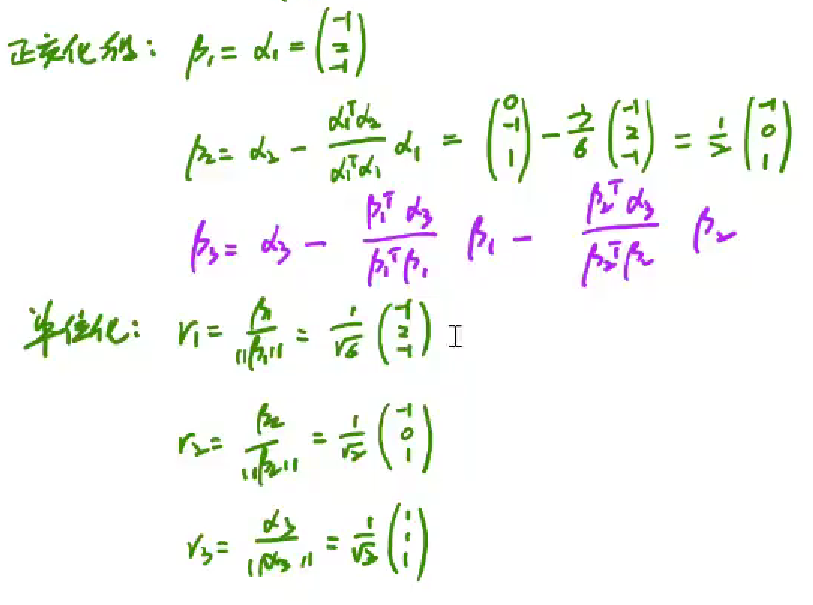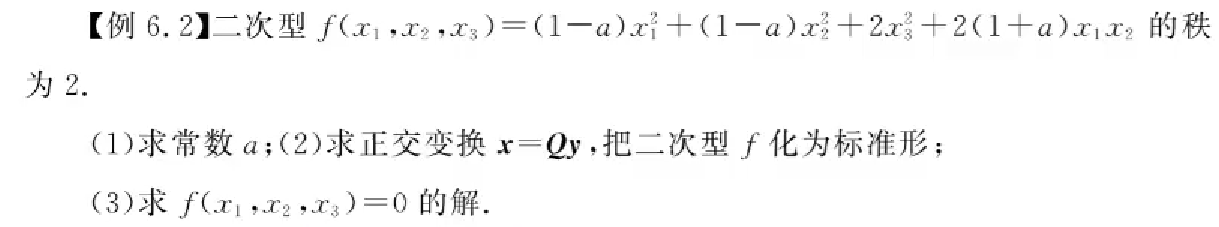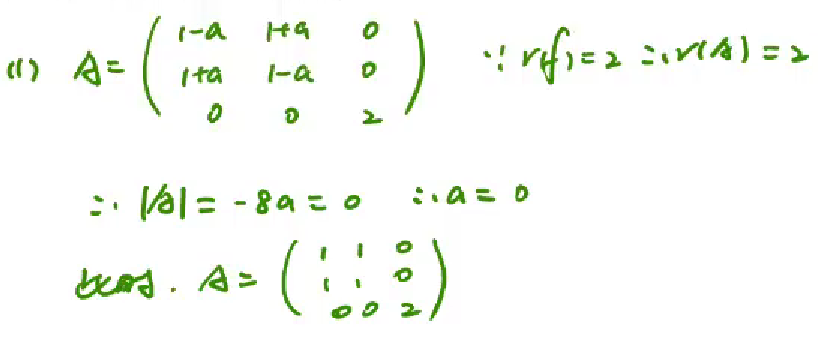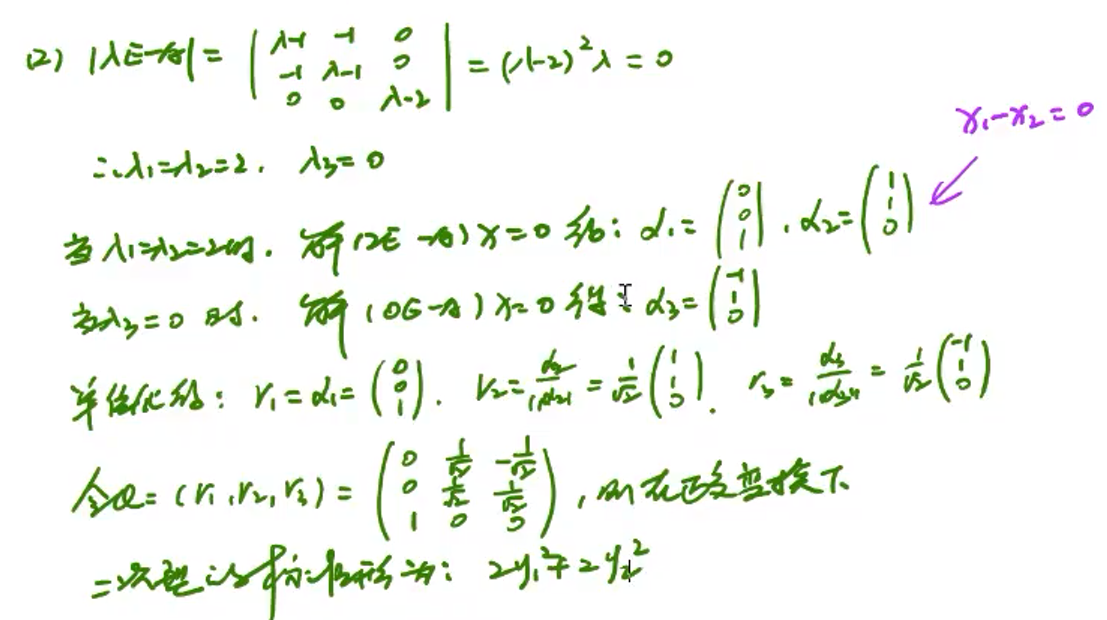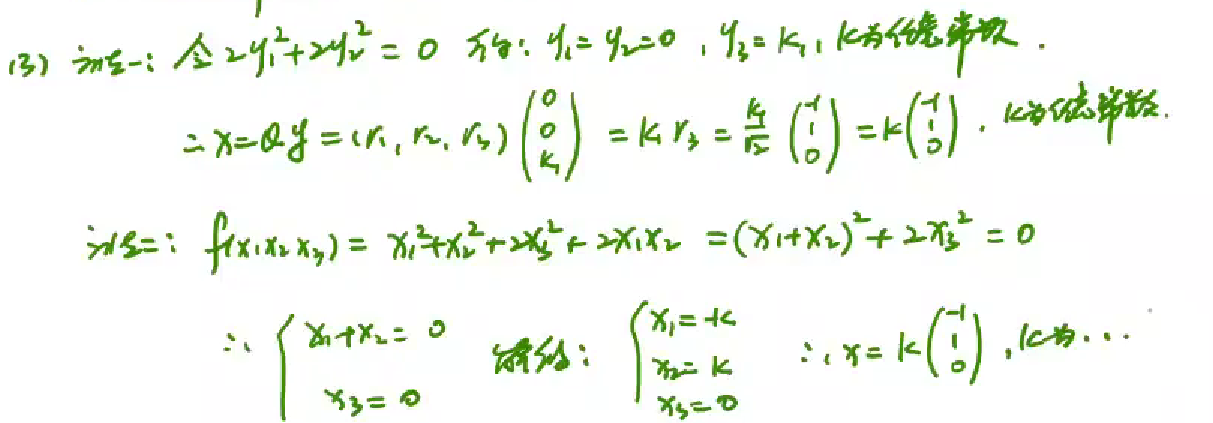线代强化

行列式

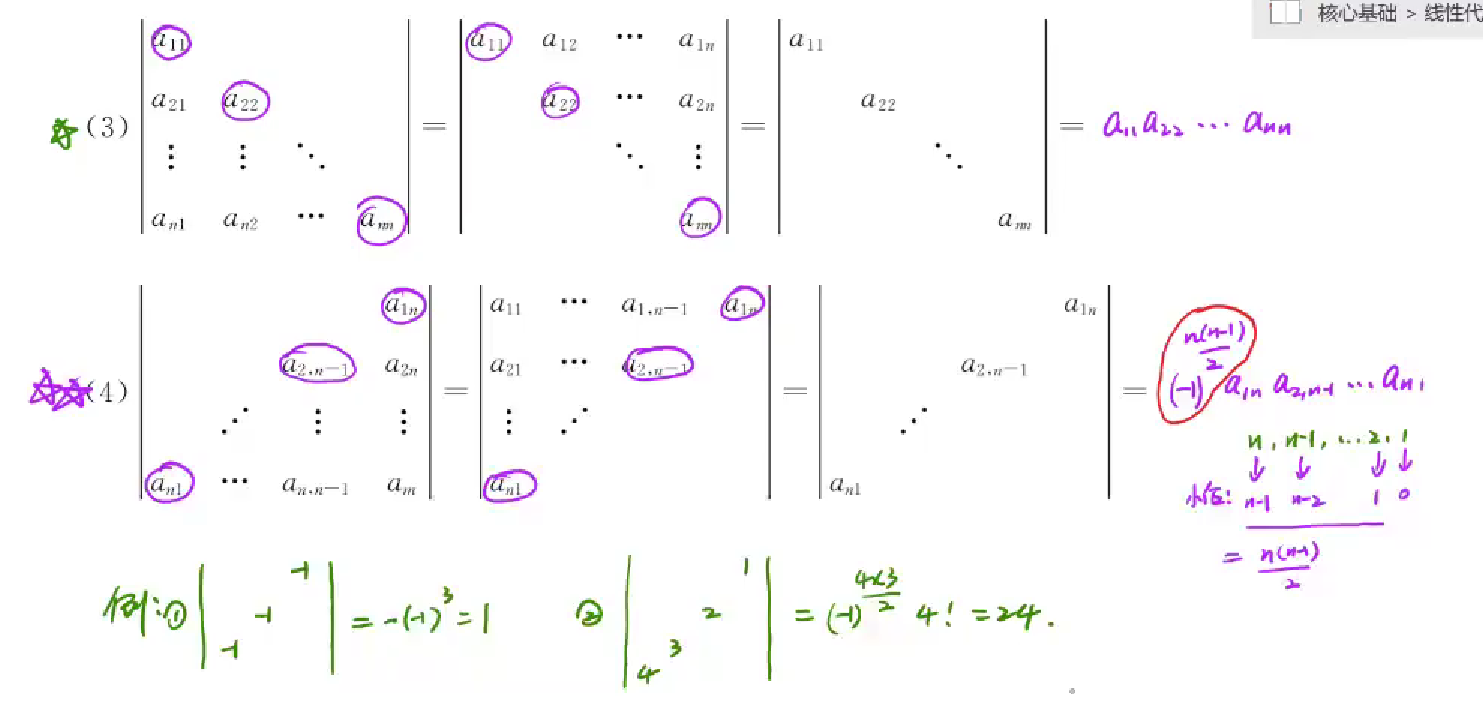
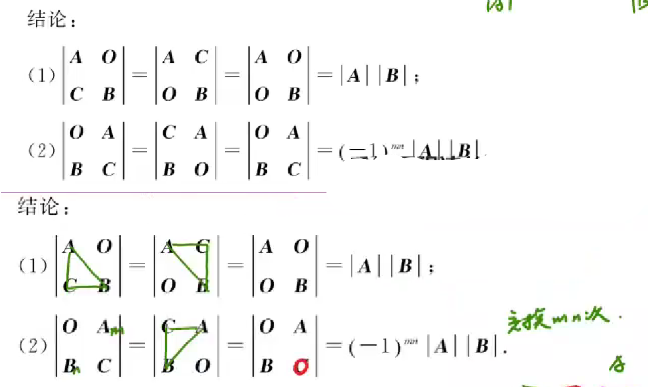
主对角线与副对角线矩阵的值

注：主对角线的矩阵的值等于对角线元素相乘，而副对角线矩阵的值等于-1^n(n-1)/2 a_1,n a_2,n-1 a_3,n-2....a_n,1

含有x的行列式的求导数，等于逐行求导，相加

证明过程很简单，不过不重要

爪型行列式的计算

注：爪型行列式的特点是，只有第一行，第一列全部不为0，像一个箭头，这种行列式转化为上三角或下三角矩阵

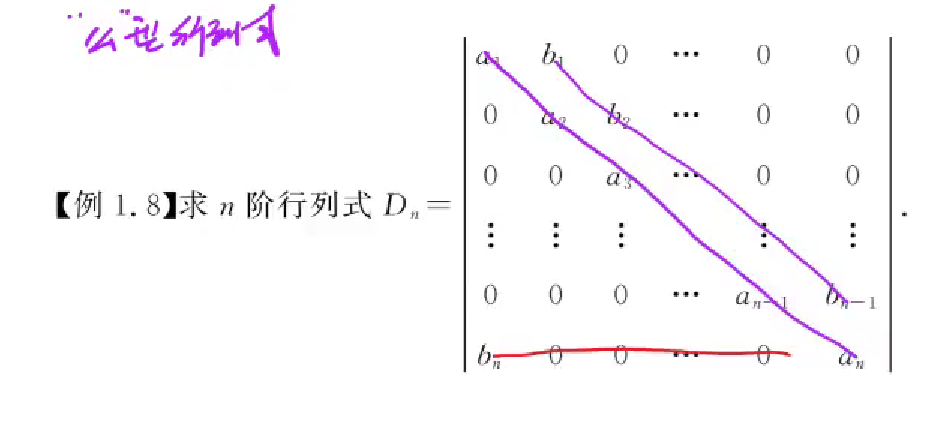
“么”型行列式计算

么型行列式按照，展开""么"那一“横”，计算就十分简单

加边法计算行列式

"加边法"适合有规律的数当加一行可以消去很多的行时，可以用加边法

梭型行列式计算

按照第一列展开 D_n=4D_n-1 - 3D_n-2 得到 D_n-D_n-1=3(D_n-1 - D_n-2) 。 递推得到
D_n-D_n-1=3(D_n-1- D_n-2)
D_n-1-D_n-2=3(D_n-2- D_n-3)
.......
D₃- D₂=3(D₂- D₁)
所以D_n-D_n-1=3^n-2(D₂ - D₁)=3ⁿ
D_n-D_n-1=3ⁿ
D_n-1-D_n-2=3^n-1
.......
D₃- D₂=3³
D₂- D₁=3²
等比数列相加得D_n - D₁ 即可计算出D_n

范德蒙行列式

$D_a=\begin{vmatrix}1&1&\cdots&1\\x_1&x_2&\cdots&x_n\\x_1^2&x_2^2&\cdots&x_n^2\\\vdots&\vdots&&\vdots\\x_1^{n-1}&x_2^{n-1}&\cdots&x_n^{n-1}\end{vmatrix}$

矩阵的基本运算

错误命题

倒推并不成立，下面是一个反例

坍缩矩阵

坍缩矩阵每次与自己相乘，有效信息都会被往外挤一次

利用坍缩矩阵性质求下列问题？

秩为1的矩阵

矩阵秩为1，对应每一行都成比例，有下面这样的一个结论
Aⁿ= l^n-1A

l 是A对角线元素之和

若A=αβ^T，r(A)=1

!

求一个矩阵与另一个矩阵的逆矩阵相乘AP^-1

已知矩阵A、P但是P的逆矩阵未知，所以可以先求出P^-1,再矩阵相乘。不过更好的方法是将P/A 竖的写在一起，将P通过列变换为E ,对于A来说，相当于乘了一个P^-1,那么A就变成了B

!

结论A^T+B^T= (A+B)^T

向量的线性组合写成矩阵的乘法

B是A的线性组合，写成两矩阵相乘形式，可以直观分离出矩阵A和所做的线性变换

 

伴随矩阵的重要性质

A^*A=AA^*=|A| E => A^*= |A| A^-1

伴随矩阵的秩 n 、1 、 0

 

抽象矩阵求逆 有难度

抽象矩阵求逆，题目中要求 (A+E)^-1
必然需要能通过题目得到一个等式 (A+E)(....)=E

(...)里的必然与A有关，相乘必然得到A²,所以先求A²

求出A²-4A=-3E，利用多项式除法凑出括号里的因式

综合表

初等矩阵、秩、分块矩阵

初等矩阵是单位矩阵经过一次初等变化后得到的矩阵

初等对换矩阵E_i,j : 由单位矩阵，交换i,j行或列得到

初等倍乘矩阵E_i(k) ：由单位矩阵，第i行或列乘k倍得到(k!=0)

初等倍乘矩阵E_i,j(k)：由单位矩阵，第i行+k*第j行得到 或 第 j列+k*第i列

重要：E_i,j(k)A是对A做 行变化；AE_i,j(k)是对A做 列变化

E_i,j^-1 = E_i,j

E_i(k)^-1=E_i(1/k)

E_i,j(k)^-1=E_i,j(-k)

E_i,j^T = E_i,j

E_i(k)^T=E_i(k)

E_i,j(k)^T=E_j,i(k)

!

AB=O

正规证明： 当矩阵A、B相乘得到零矩阵，可以想象A_(mxn)是系数矩阵，B_(nxm)是解向量矩阵；一个齐次线性方程组的线性无关解向量数=n-r(A)
简便记忆：标准型记忆法

例题：

重要结论：r(AA^T)=r(A^TA)=r(A)

分块矩阵的结论

合理利用矩阵分块，将矩阵分块成更小的方阵，可以简便计算

二阶矩阵的逆矩阵

主 对调；副 变号

左行右列，BA=C

将矩阵B看做一种线性变换。
BA可由 A经过B行变换得到；
但是反过来A不一定可由BA经过B^-1行变换得到，因为B不一定可逆。
所以下面这个式子中，BA可以被上面的A经过行变换后逐项消去

例题

向量组

向量组等价

矩阵等价，只需要两矩阵秩相等；
向量组等价，需要两向量组A: α₁,α₂,α₃...α_n与向量组B：β₁,β₂,β₃...β_m,可以互相线性表示，也就是r(A,B)=r(A)=r(B),对于A来说B的任何一个向量加入都是混子，对于B来说A的任何一个向量加入都是混子

问题：已知α₁,α₂,α₃线性无关，判断下列是否线性无关？

请判断α₁+α₂+α₃，α₁+2α₂-3α₃，α₁+5α₃是否线性无关？

思路1：凑系数k1,k2,k3，当只有k1,k2,k3全为0时才满足k1(α₁+α₂+α₃)+k2(α₁+2α₂-3α₃)+k3(α₁+5α₃)=0,这时向量组就是线性无关的，都是无法相互消去的

思路2：像这种比较难凑，写成矩阵相乘，将线性变换用矩阵写出，然后根据r(α₁,α₂,α₃)=3，所以相乘矩阵的秩=后面的线性变换矩阵的秩，计算行列式，如果不等于0，说明满秩，从而向量组线性无关

用定义法证明向量组线性无关

解：令k₁α₁+k₂α₂+k₃α₃=0 ①
两边同乘Ak₁Aα₁ + k₂Aα₂ + k₃Aα₃= k₁α₁ + k₂(α₁ + α₂) + k₃(α₂+α₃)=0 ②②-①得k₂α₁ + k₃α₂=0 ③两边再次同乘Ak₂Aα₁ + k₃Aα₂= k₂α₁ + k₃(α₁+α₂) =0 ④④-③得k₃α₁=0，由于α₁!=0,所以k₃=0,往回代入，求得k₂=0，k₁=0,所以三个向量线性无关

求一个向量在以另一组向量作为基底下，的坐标

就是求x₁α₁ + x₂α₂ + x₃α₃ = α，α在基底下的坐标就是(x₁,x₂,x₃)
1.可以直接列方程解；2.也可以作为非齐次方程求解

注：一组基，一定是一组线性无关的向量

过渡矩阵

AP=B,则称，A过渡到B的过渡矩阵是P

线性方程组求解

典型例题

若AB=O,则r(A)+r(B)≤n

典型例题2

两个方程有公共解问题

两个方程组有同解问题

①两方程组，同解，那么基础解系个数一定相等，分别求出两线性方程矩阵的秩；
②然后再根据其中一个方程，求出解系，代入另外一个方程，使得等式恒成立
③求出结果，带回去验证秩是否符合

公共解、同解与特征值特征向量

对于任何一个矩阵，矩阵对角线系数之和=它的特征值之和


解特征值，特征向量的方法

方法1.常规方式，解非齐次方程

方法2.技巧性方法
①.这题的矩阵A可以拆开为一个秩为1的矩阵 B-E
②r(B)=1，特征值0, 0，λ₃
③利用对角线元素之和=特征值之和=6，所以λ₃=6
④A=B-E，Aα=Bα-Eα ，λ_Aα=λ_Bα - α，所以λ_A=λ_B-1，对应特征值是一样的

各种矩阵的特征值

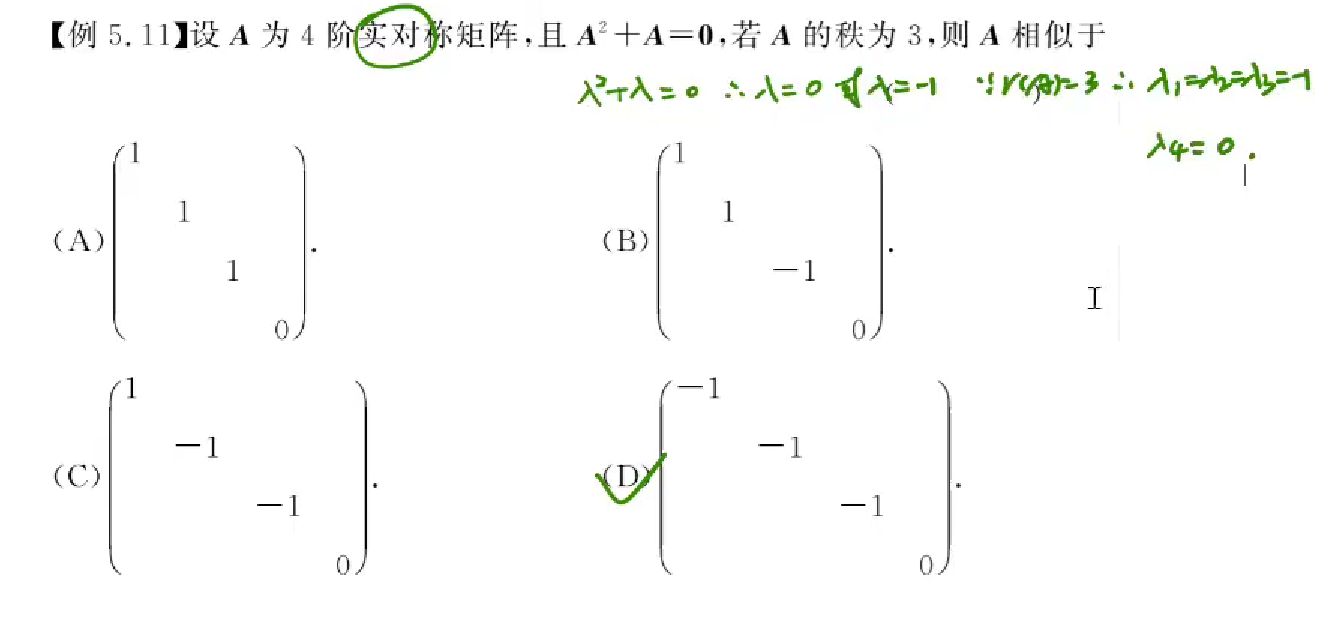
很经典的一道题

考察伴随矩阵的特征值之和

判断一个矩阵A可否对角化

1.证明存在三个线性无关的特征向量，能组成P，使得P^-1AP=∧

特征值不是重根的特征向量的组合，求其特征值

对于P=(α₁ α₂ α₃), 它是A的特征向量组成的矩阵，对应的特征值分别为λ₁、λ₂、λ₃，则有AP=λP ==> P^-1AP=∧_p

典型例题

实对称矩阵与二次型的标准型

实对称矩阵性质

• 若A是实对称矩阵，则一定可以对角化即P^-1AP = ∧，且不同特征值对应的特征向量一定是正交的；相同特征值对应的特征向量就只是线性无关不一定相互正交。
• 实对称矩阵进行相似变换的矩阵P的可以正交化，单位化为一个正交矩阵Q，可以使得Q^-1AQ=∧
• 又因为正交矩阵有性质Q^-1=Q^T，所以Q^TAQ = ∧，称之为合同对角化

例题

这里A有两个特征值，0,-1。又因为r(A)=3，所以他的对角矩阵的秩也等于3，那么只能是3个-1

矩阵的正交化合单位化

求方阵的幂次Aⁿ

方法1.利用方阵成比例，如果方阵成比例，r(A)=1, Aⁿ=l^n-1A

方法2.利用对角化，P^-1AP=∧，则A=P∧P^-1,则Aⁿ=P ∧ⁿ P^-1

二次型的基本概念

1.一般型 f(x)=X^TAX
2.标准型 X^TAX = X^TP^-1 ∧ PX = Y^T∧Y 【X=PY就是正交变换，P为正交矩阵】
3.规范型 换元对角线系数全为1

67
解二次型问题

解二次型，一般先转换为标准型，解出Y，利用正交变换解出X

例题

二次型的正定性与合同

正定二次型的判定

二次型f(x)=X^TAX,对于任意x取值，都为正，就称之为正定

所以正定的二次型，配方转换为标准型(只有平方项)，那么平方项系数都大于0

另外还能通过各阶主子式都大于0，确认正定

区分等价、相似、合同之间的关系

假设P、Q可逆

等价：PAQ=B，称A与B等价

相似：P^-1AP=B，称A于B相似

合同：P^TAP=B，称A与B合同【注：一般只考察二次型的合同】

那要如何判断两个二次型是否合同？

1与二次型矩阵合同的矩阵一定也是一个对称矩阵因为P^TAP=B，则B^T=P^TAP=B，得先满足这个条件
2.满足上述条件后，如果两个二次型对应的标准型的正负号相同(特征值的符号相同)，那么就是这两个二次型合同的

若A是方阵，α是向量则，Aα，任然是一个向量

典型例题

---

二次型正负定性的判定

判断一个对称矩阵是否正定：
1.正交变换法化为标准型，看得到标准型矩阵，对角线的特征值是否都>0
2.配方法化标准型，看得到的标准型矩阵，对角线的数是否都>0
3.看正惯性指数，看是否全都是正的
4.看A的各阶主子式是否都为正
判断一个对称矩阵是否负定：
1.前三条与上面正好相反
2.看A的各阶主子式，奇数阶为负，偶数阶为正，那么就是负定