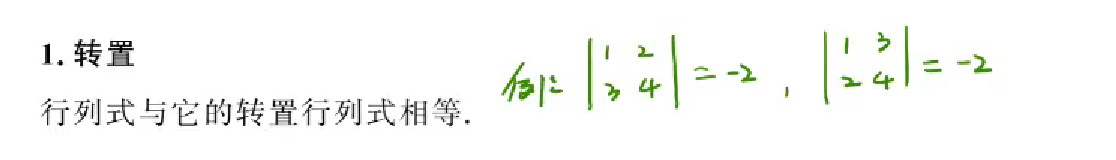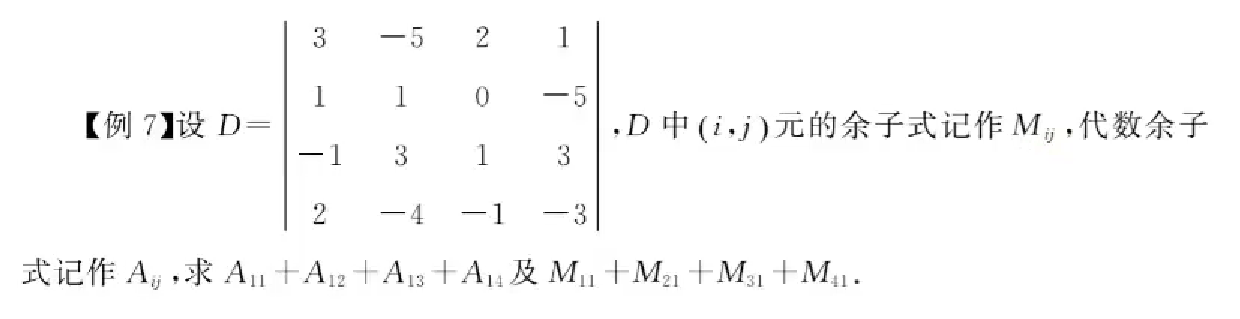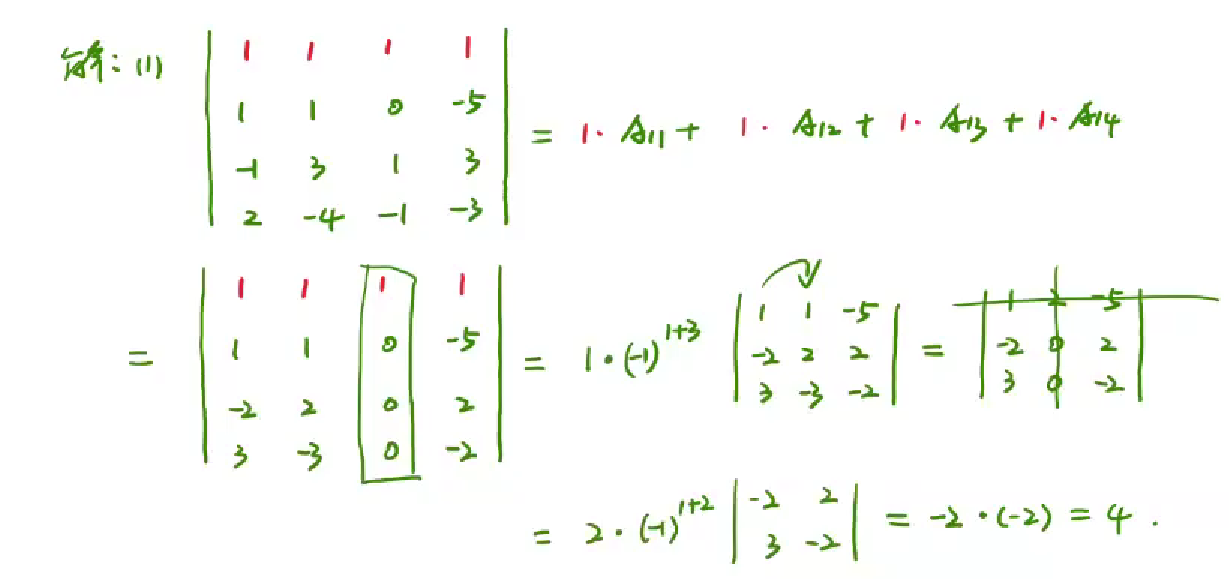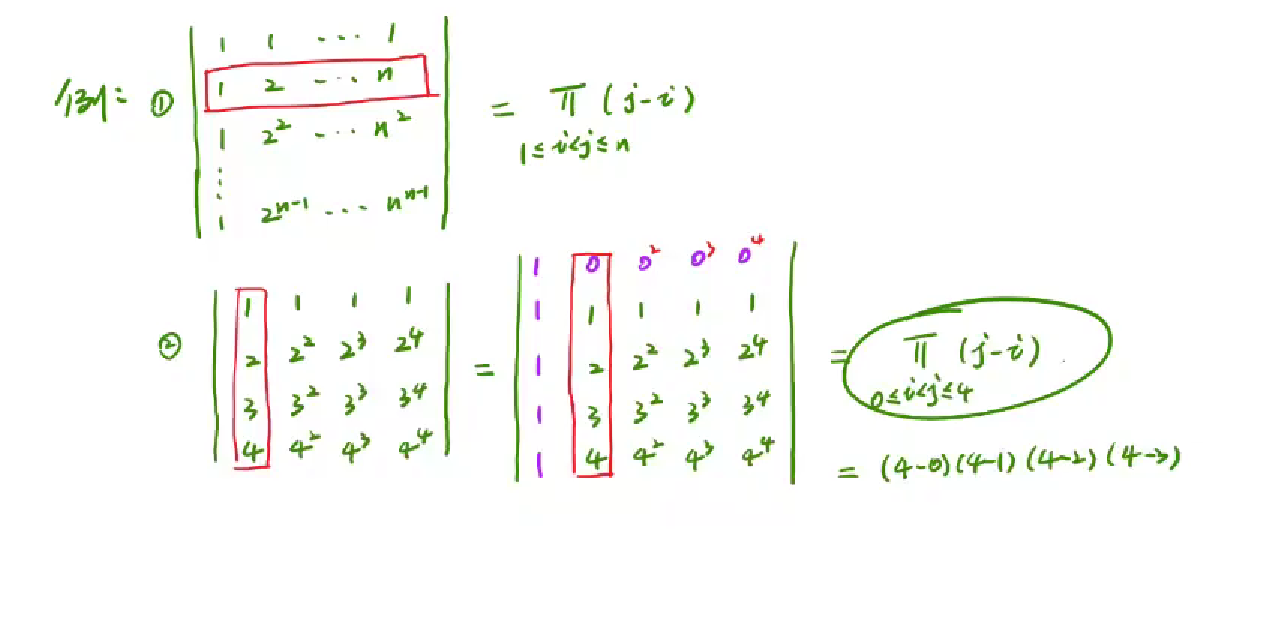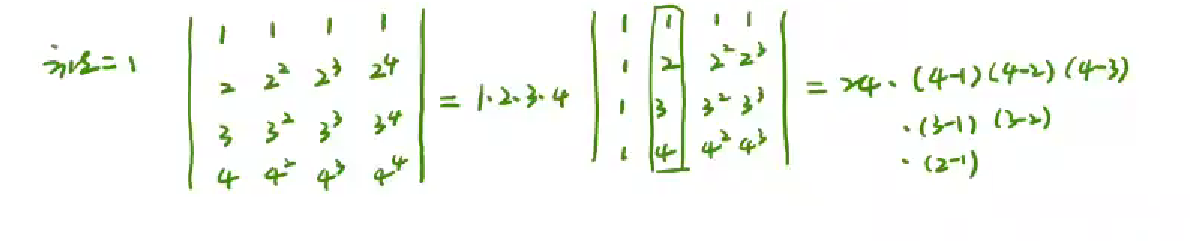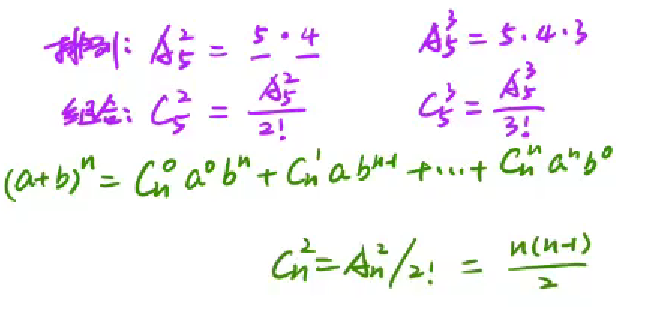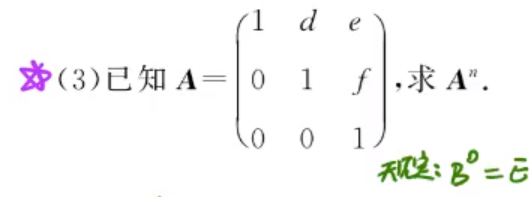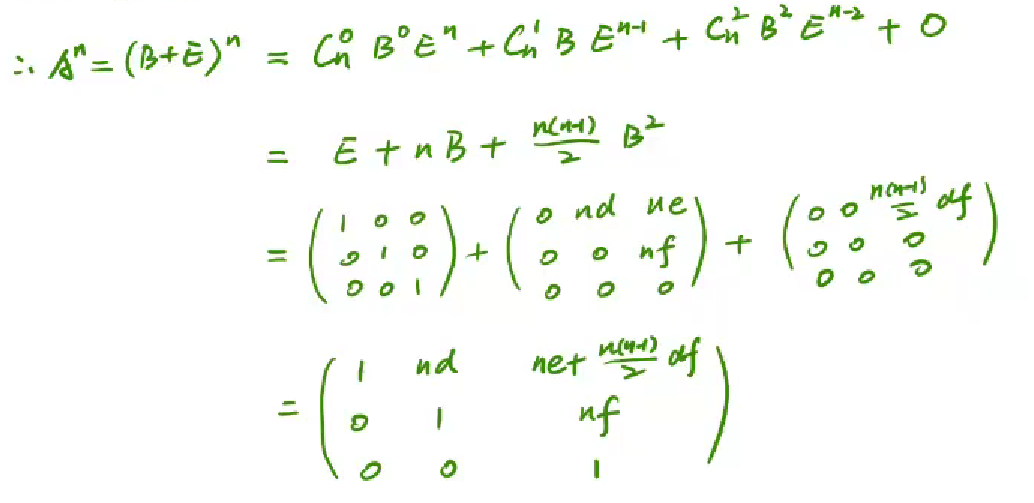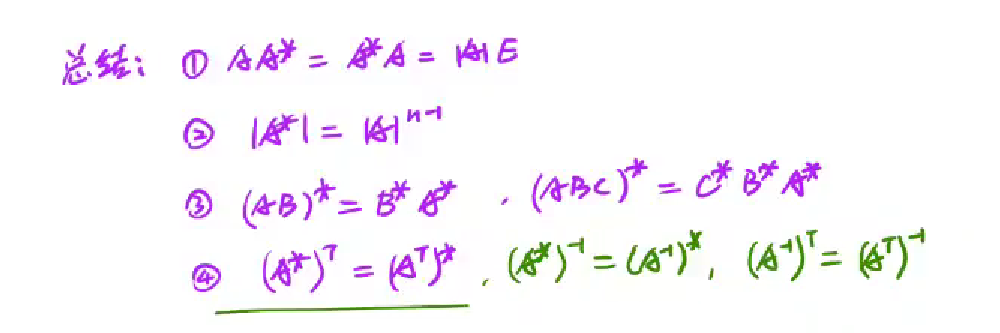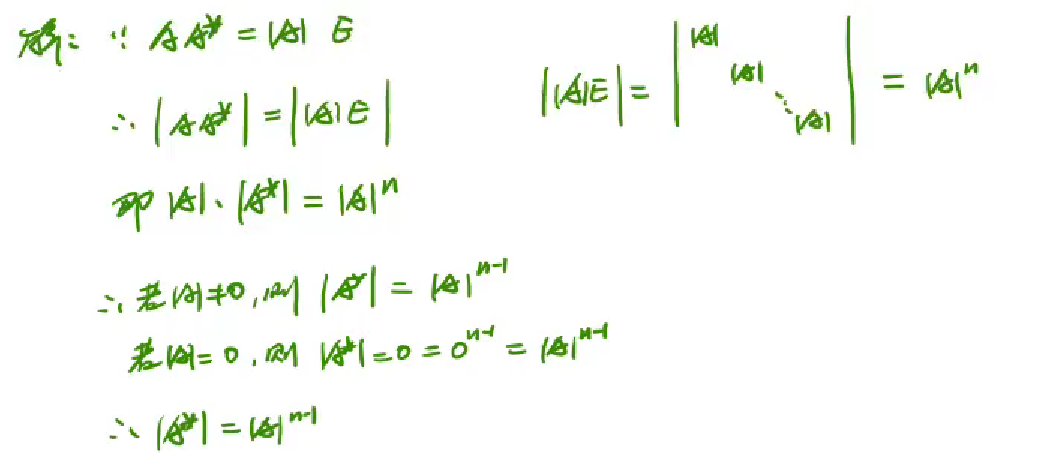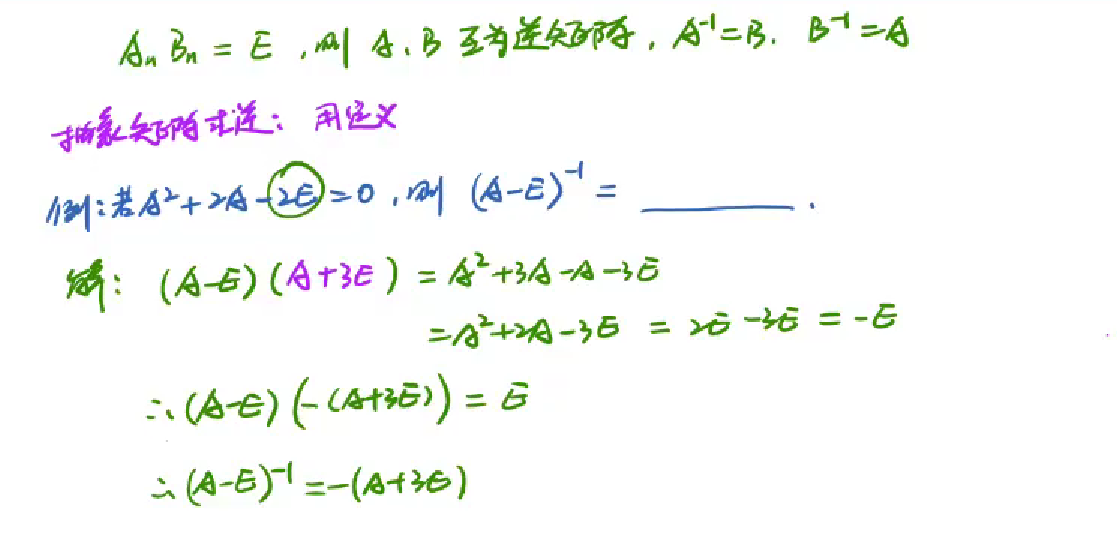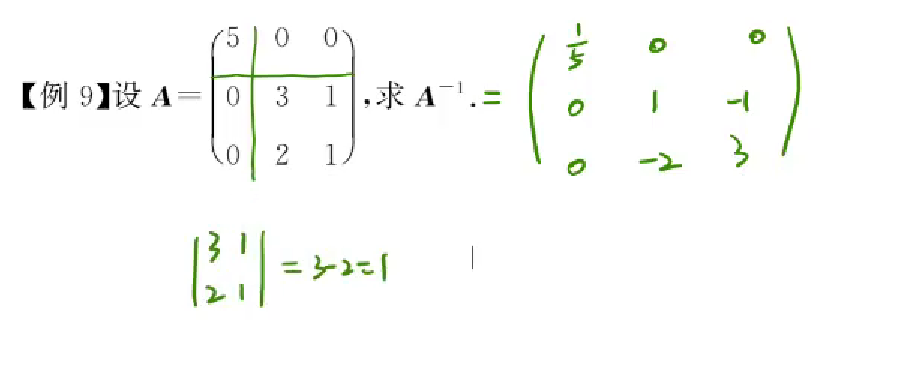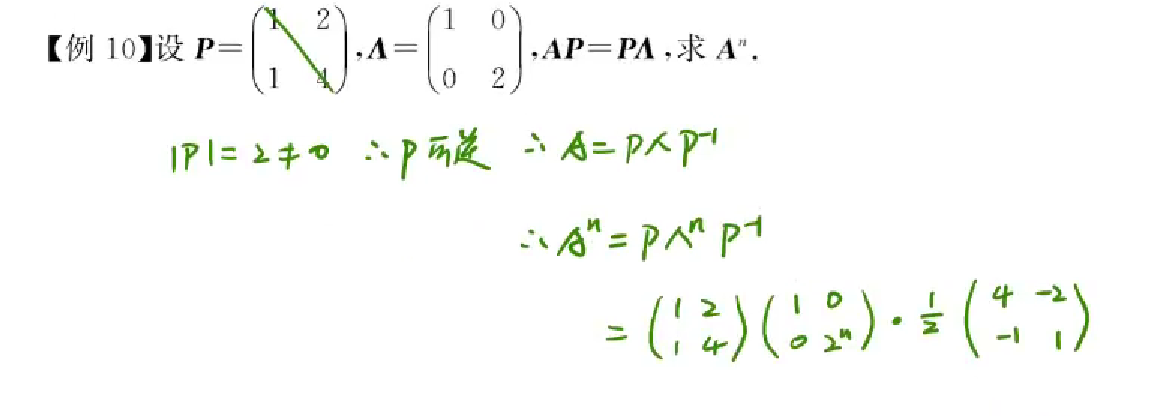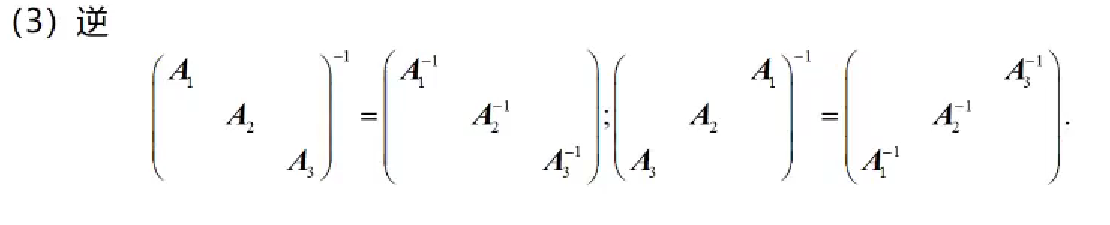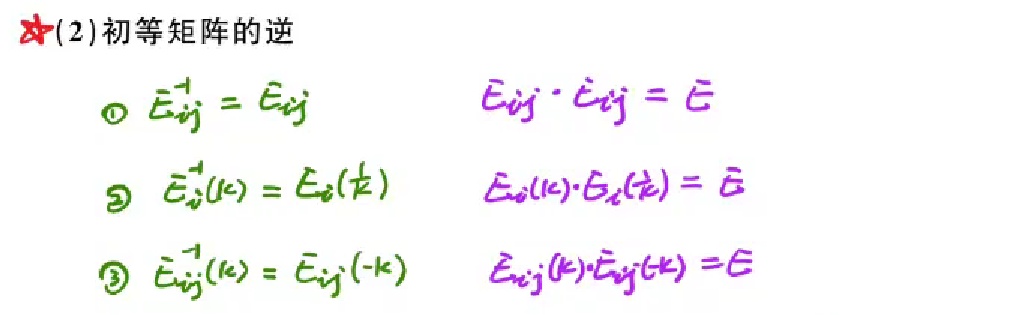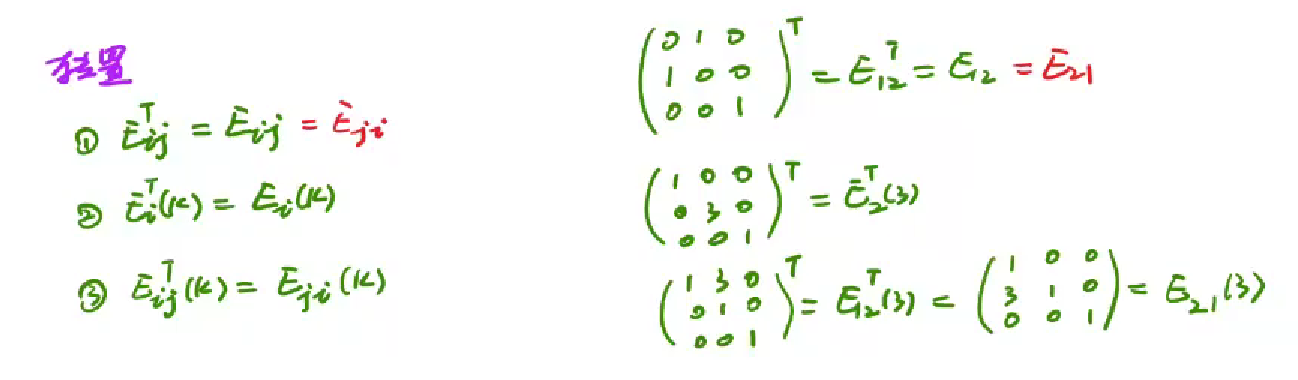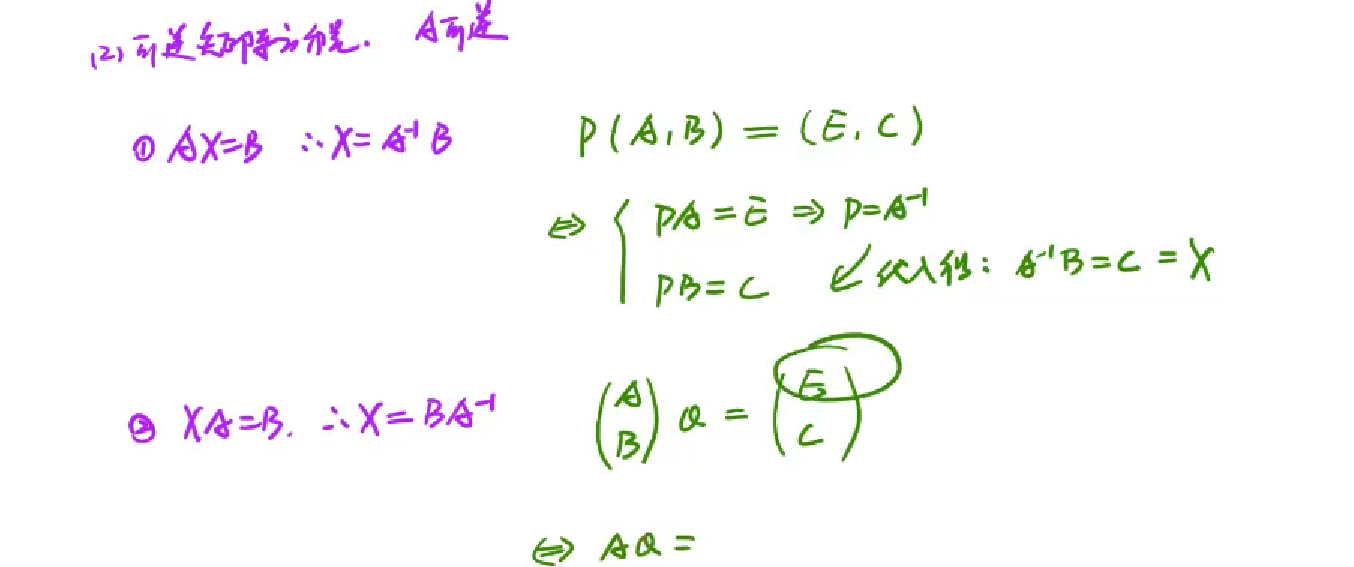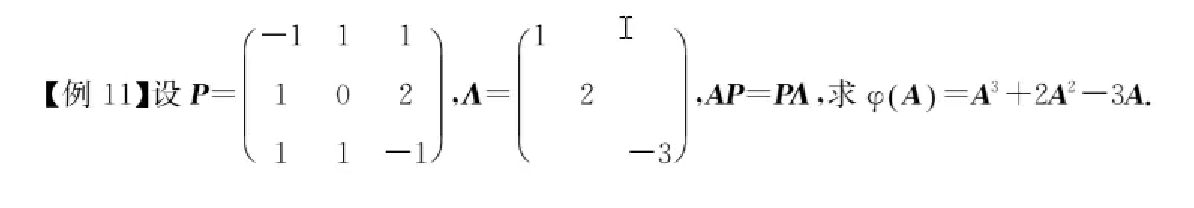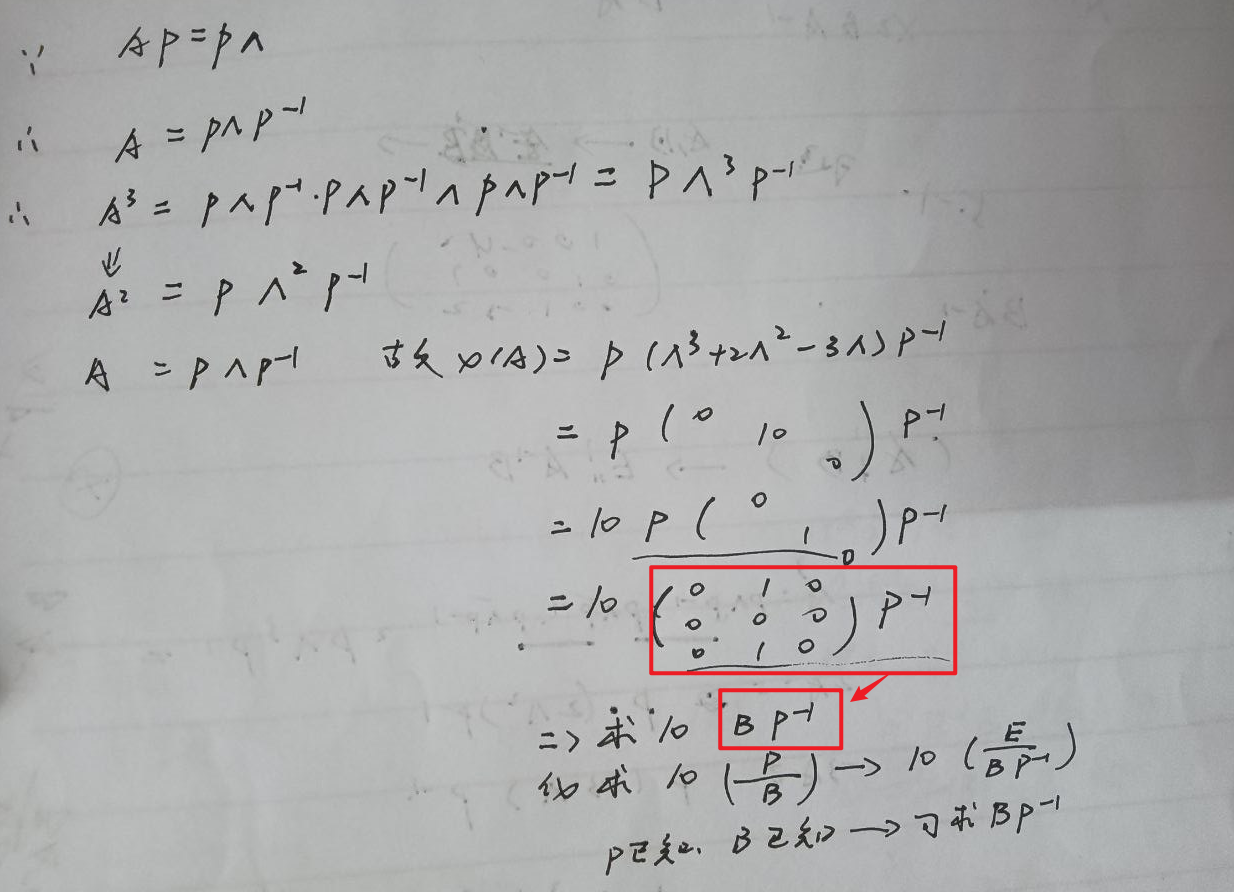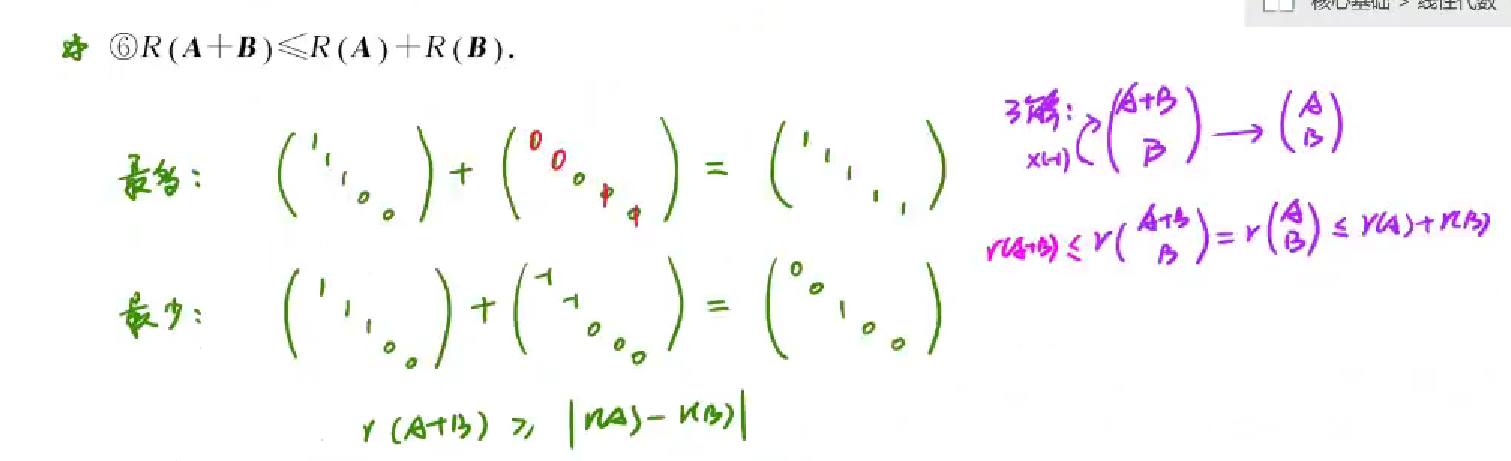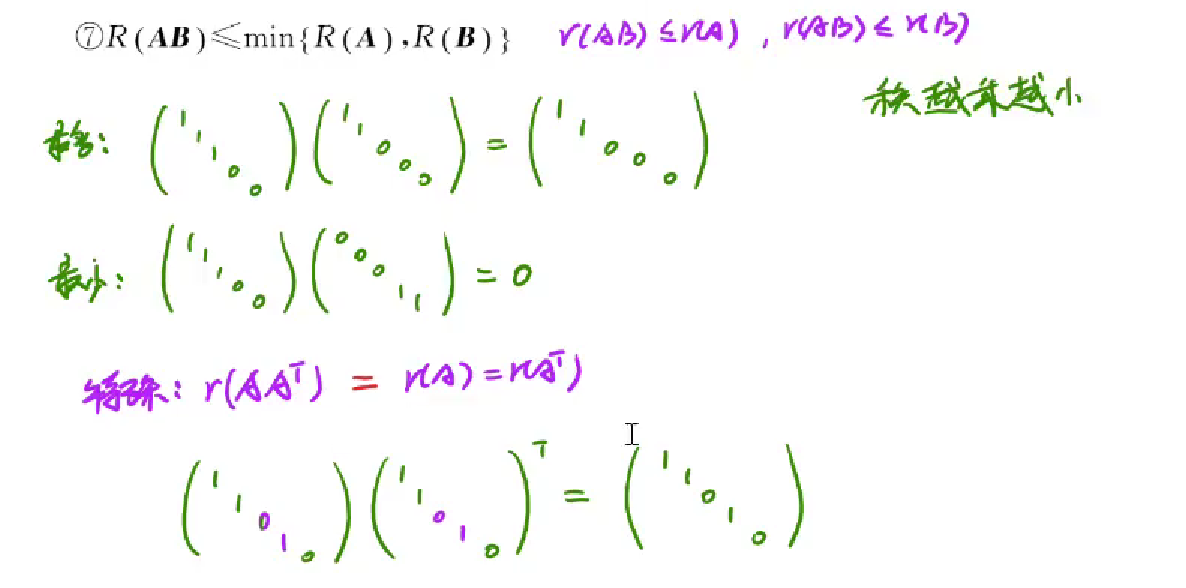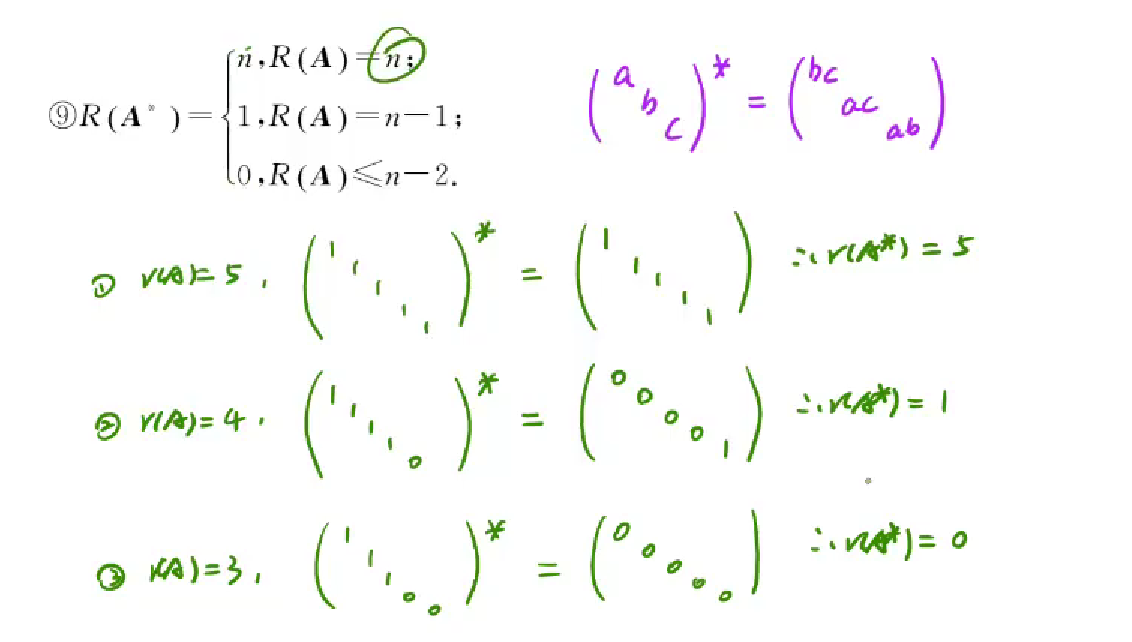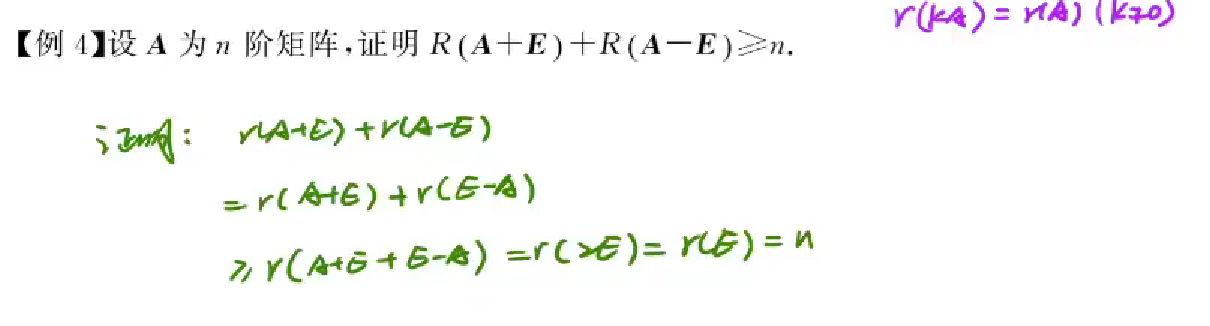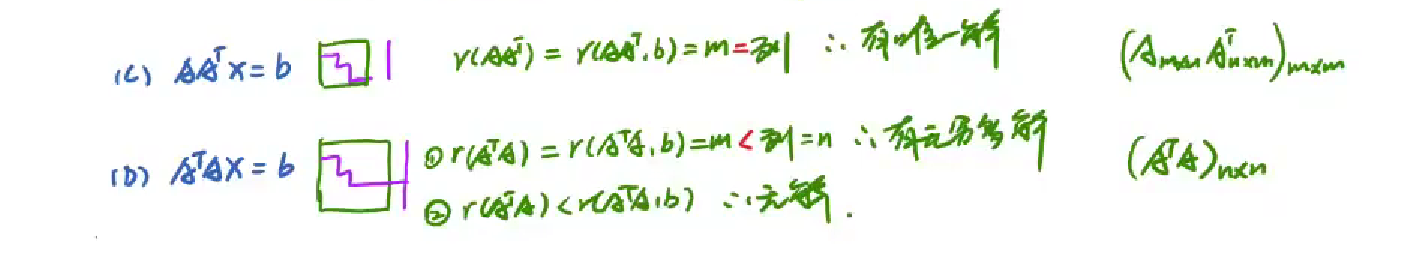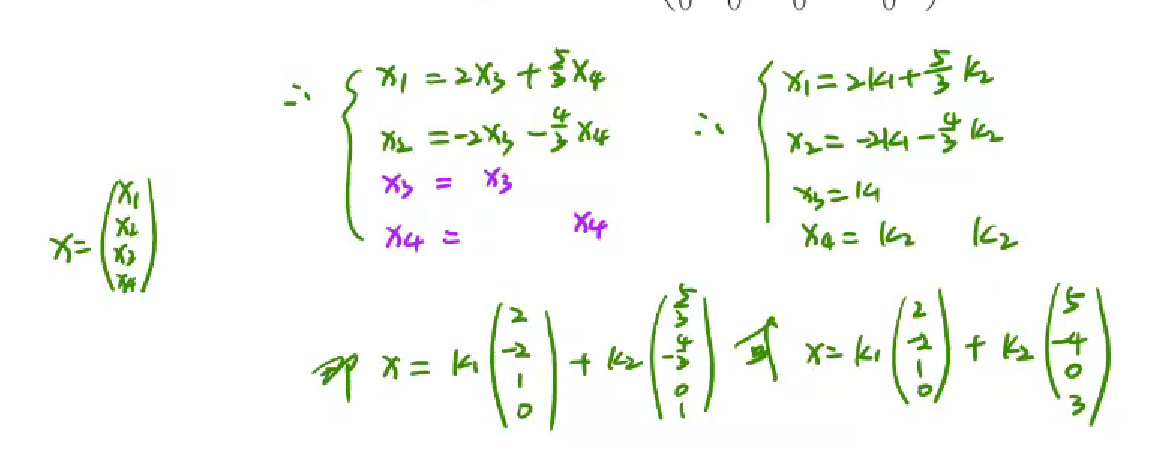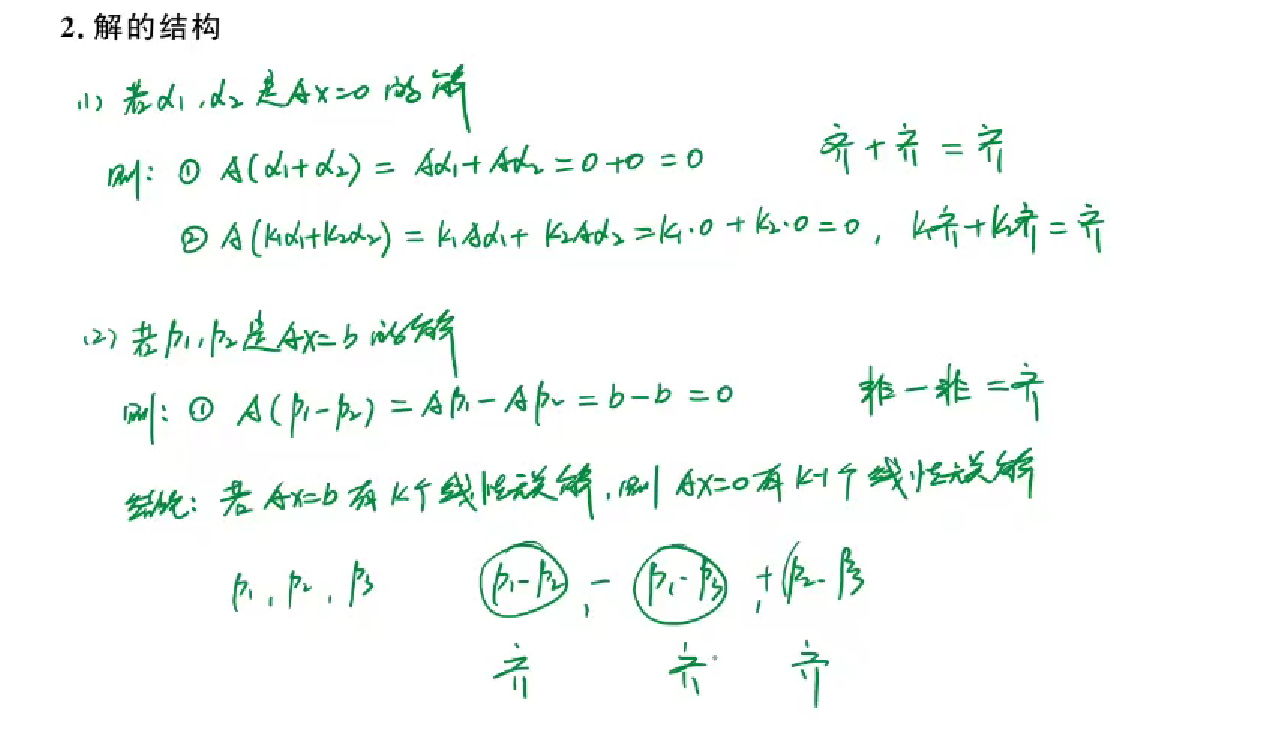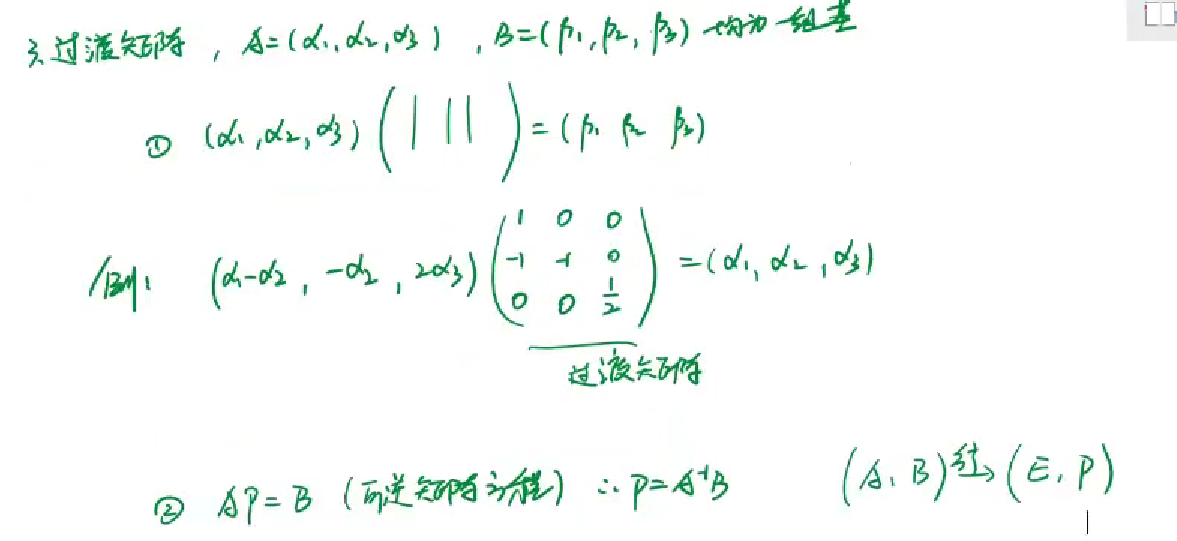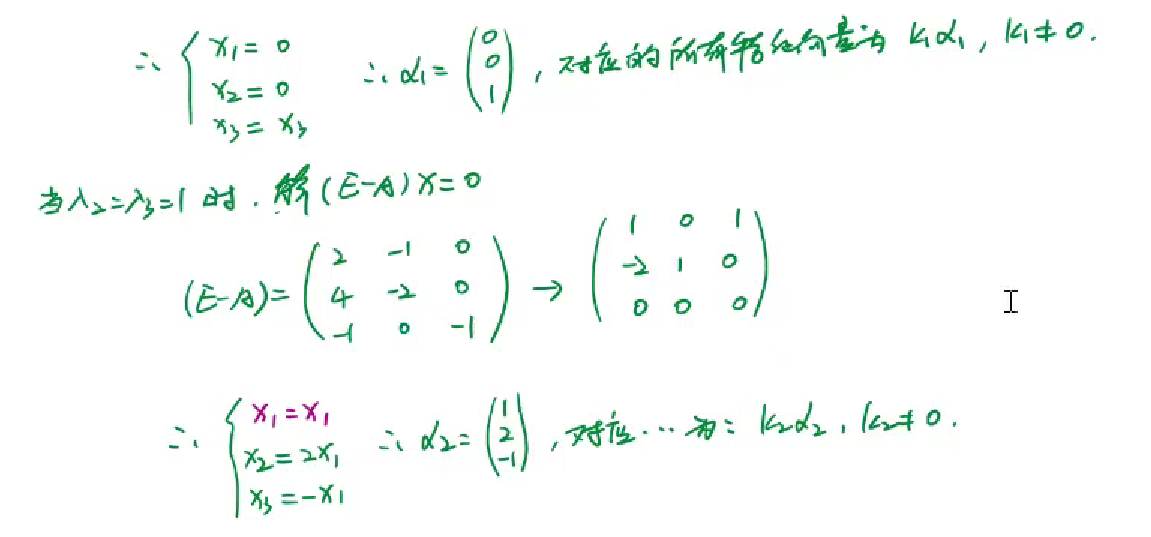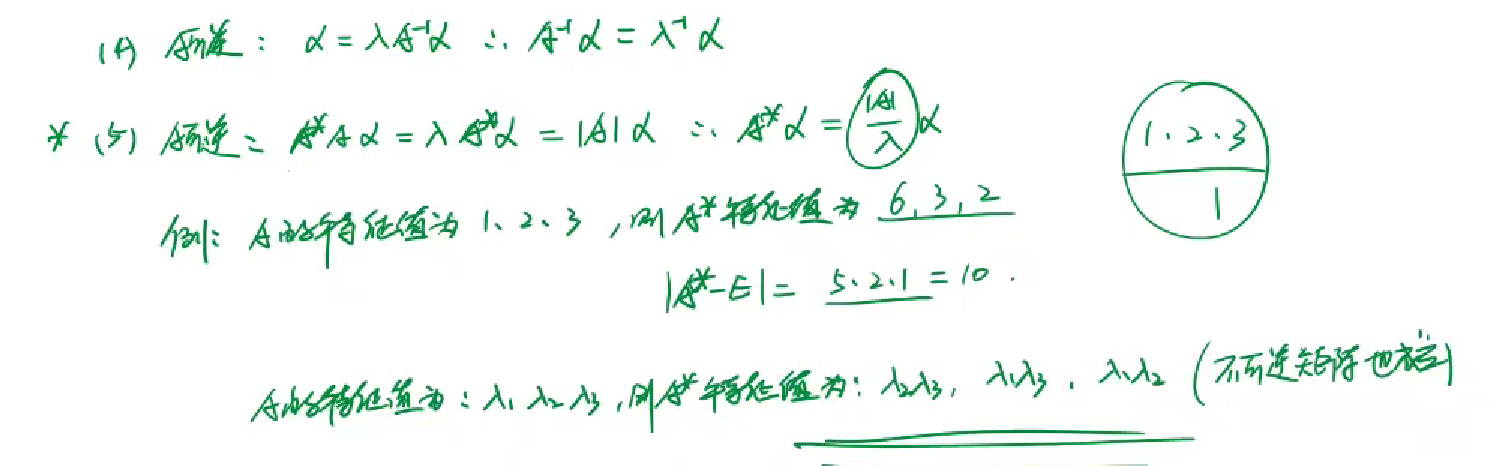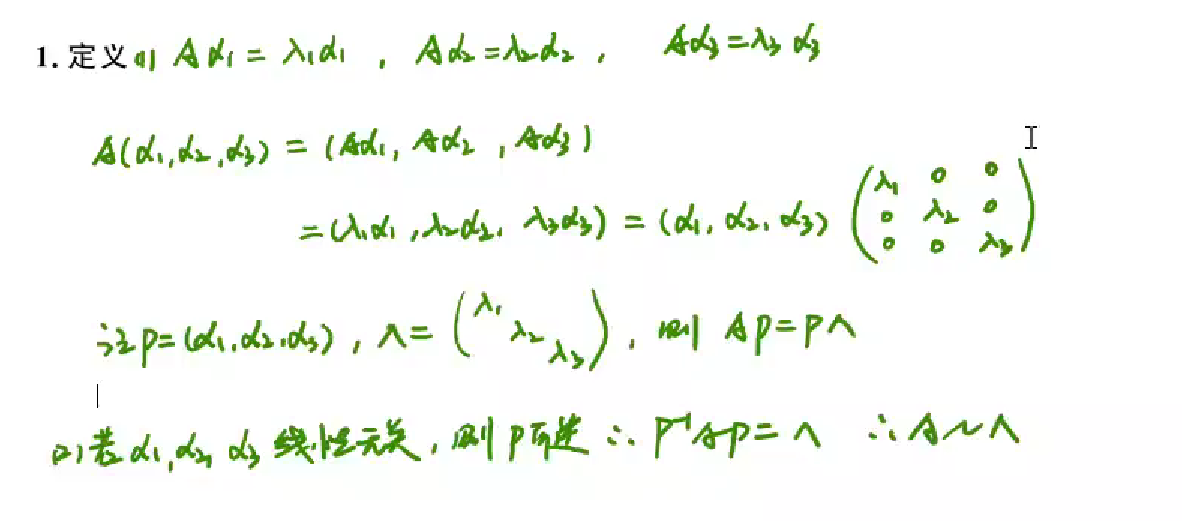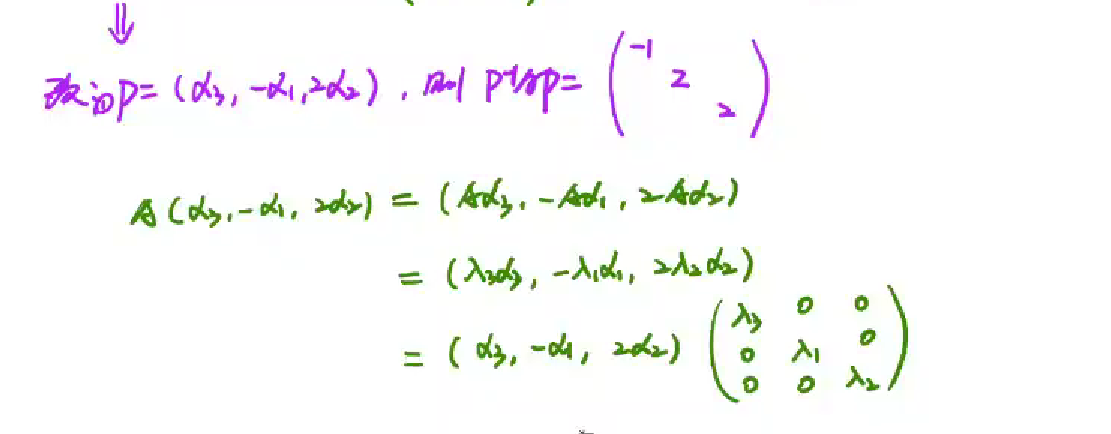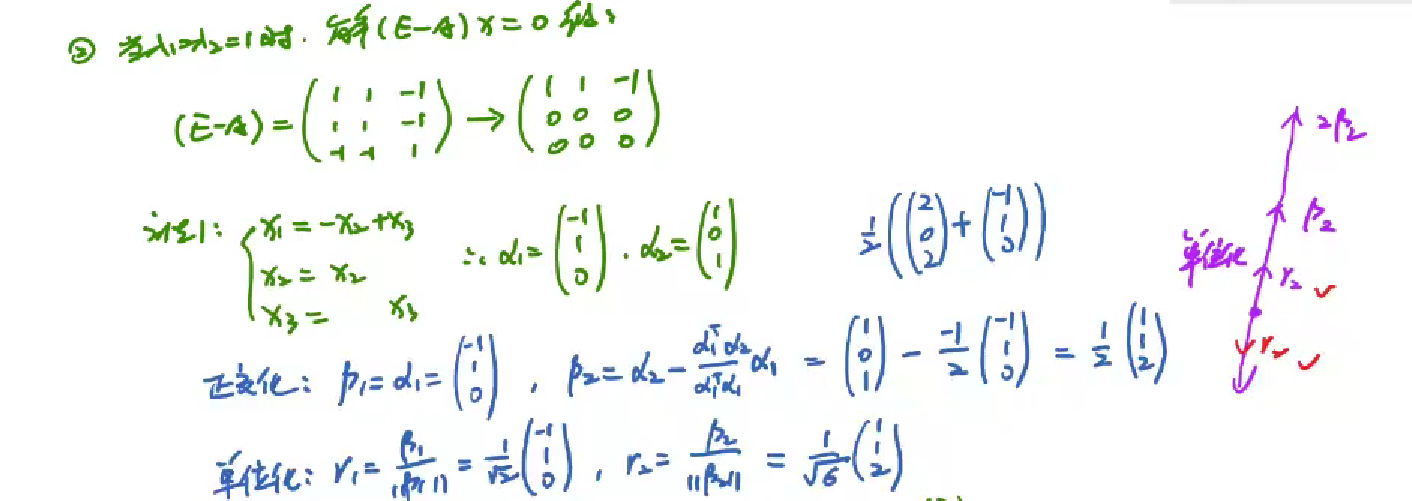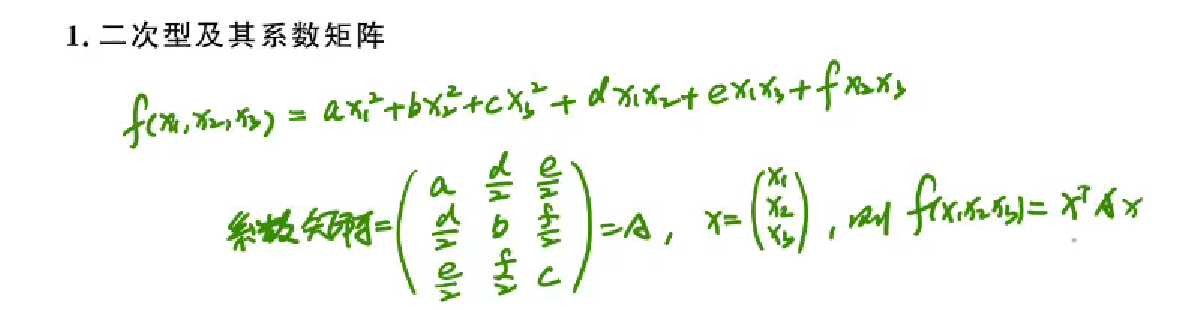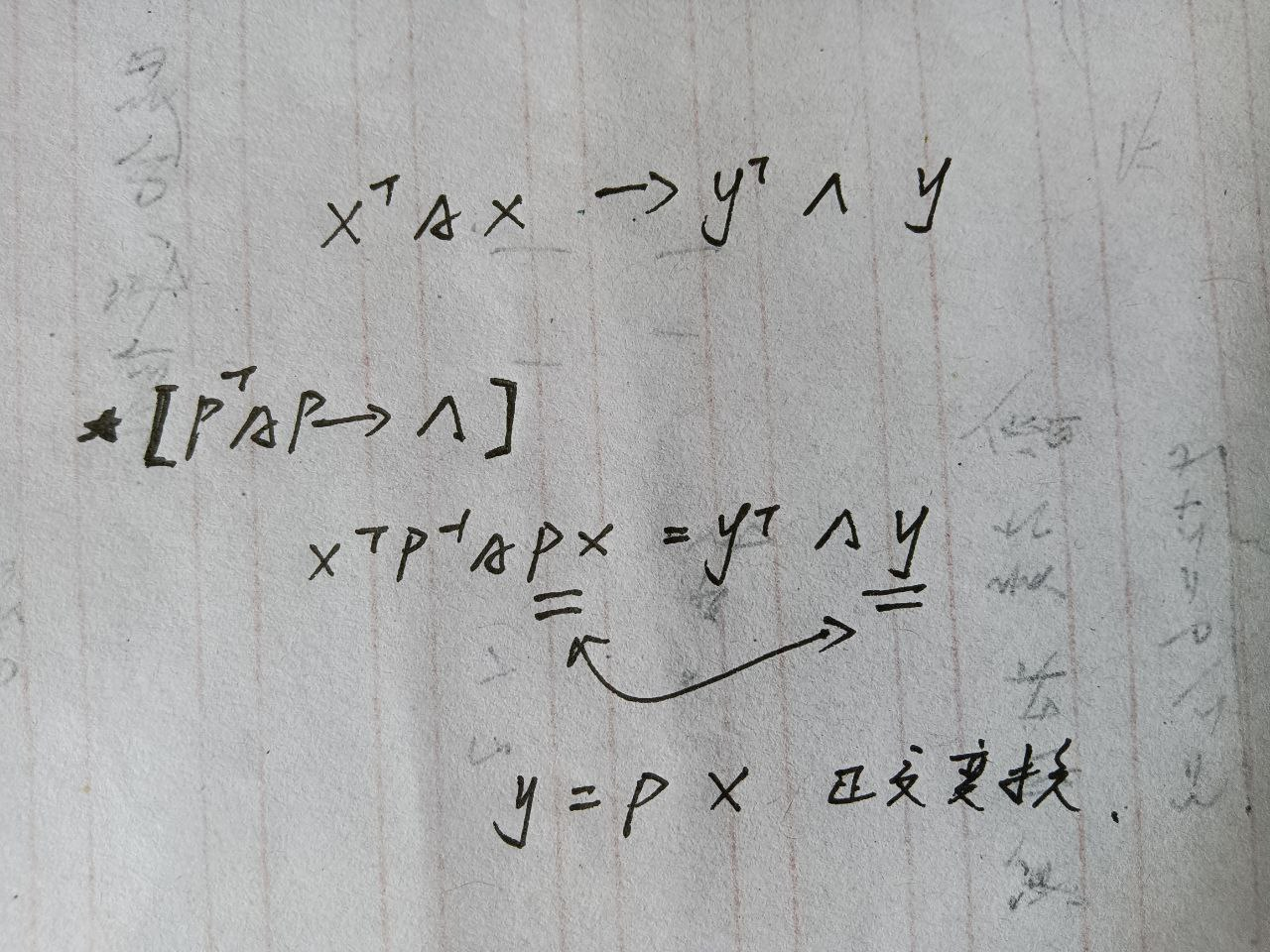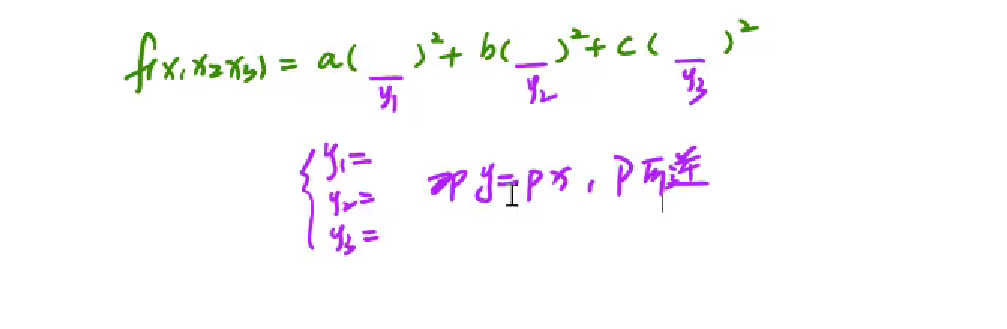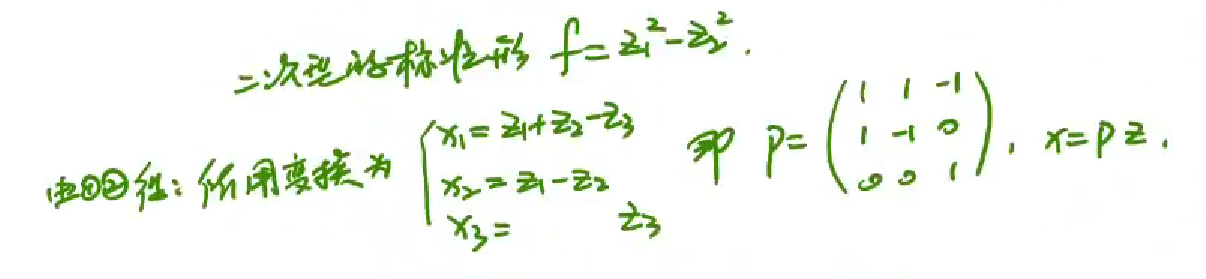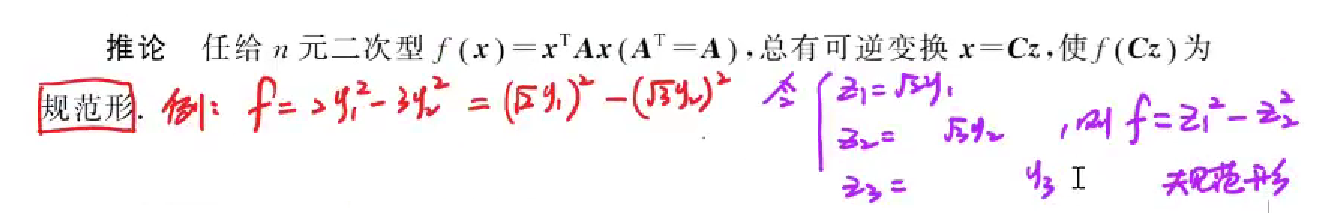01-行列式的定义与性质

行列式背景

1
2
3
对于一个二元方程组，每次都要求解就特别麻烦。
为了更加快速的找到方程的解，人们寻找规律，发现解的通式如下
但是通式难以记忆，所以将这种计算规律用行列式表示，规定行列式计算方式

image.png

image.png

逆序数

1
重要结论:一个排列中任意的两个元素对换，排列的奇偶性改变

image.png

n阶行列式的定义

1
2
3
4
5
6
行列式是一个数
行列式计算方法是：
	1.取数相乘: 取n个不同行不同列的数 相乘 --> 所以n!种取法，就有n!项
	2.冠以符号: 每一项(n个数相乘),将里面的元素，按列排好，然后数 列序号的逆序数τ，
		-(1)^τ
	3.全部相加: 将所有项n!项相加

image.png

1
2
3
4
5
6
7
8
9
10
11
12
按照行列式定义，因为行列式的每一项都是有不同行不同列的n个数相乘
假如取1行1列的数-->x
那么画个十字线，十字线上的数都不能再取
题目要求行列式结果中x^3的系数

排除法:
假如先取1，画十字线，发现其他行最多只能取到两个x，构不成x^3
假如先取2，同理不行
所以只能取x或x+3
 取x+3,只有一种情况，可行
 取x,第二行只能取x,第三行只能取x,第四行只能取x，那么x^4不符合。

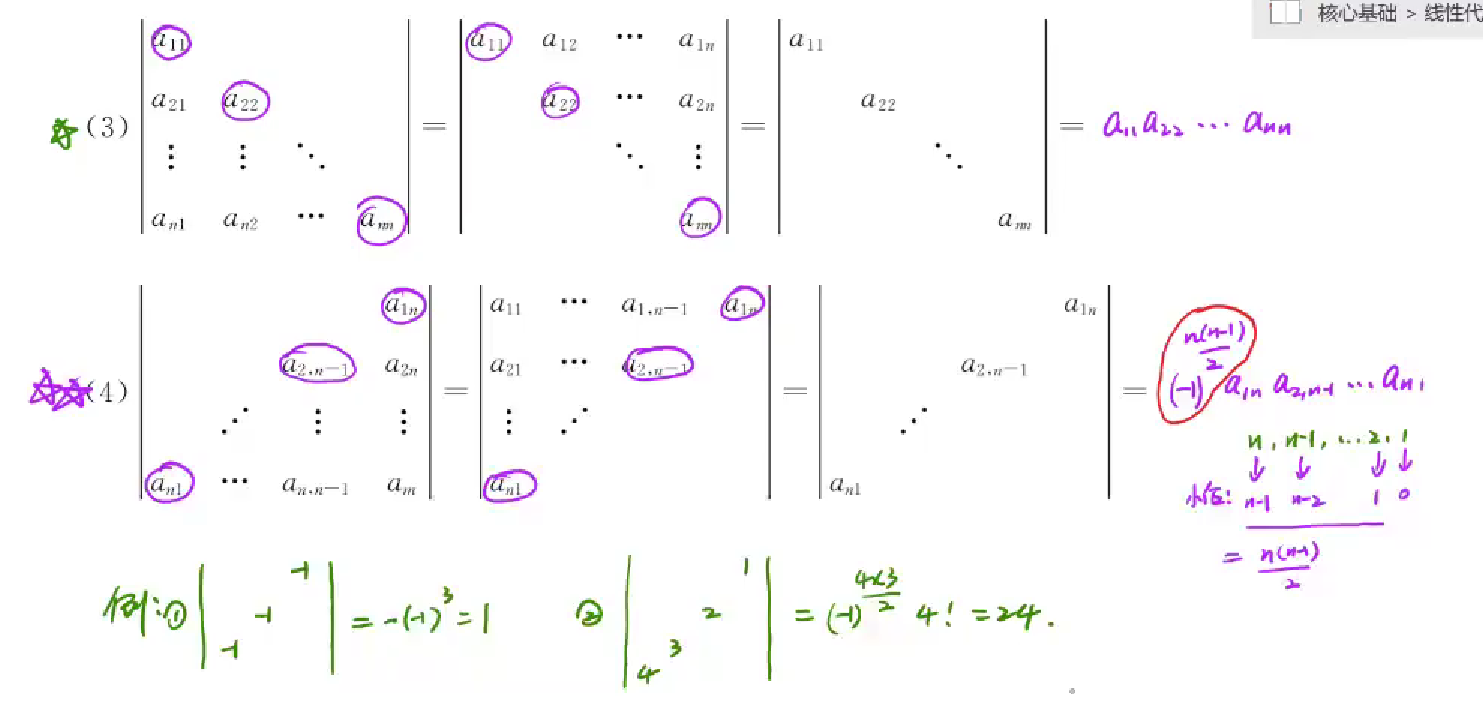
image.png

主对角线与副对角线矩阵的值

注：主对角线的矩阵的值等于对角线元素相乘，而副对角线矩阵的值等于-1n(n-1)/2 a1,n a2,n-1 a3,n-2....an,1

image.png

行列式的性质

转置

image.png

交换

交换一行实际上是对每一项的逆序数发生改变，导致全部项的正负性改变
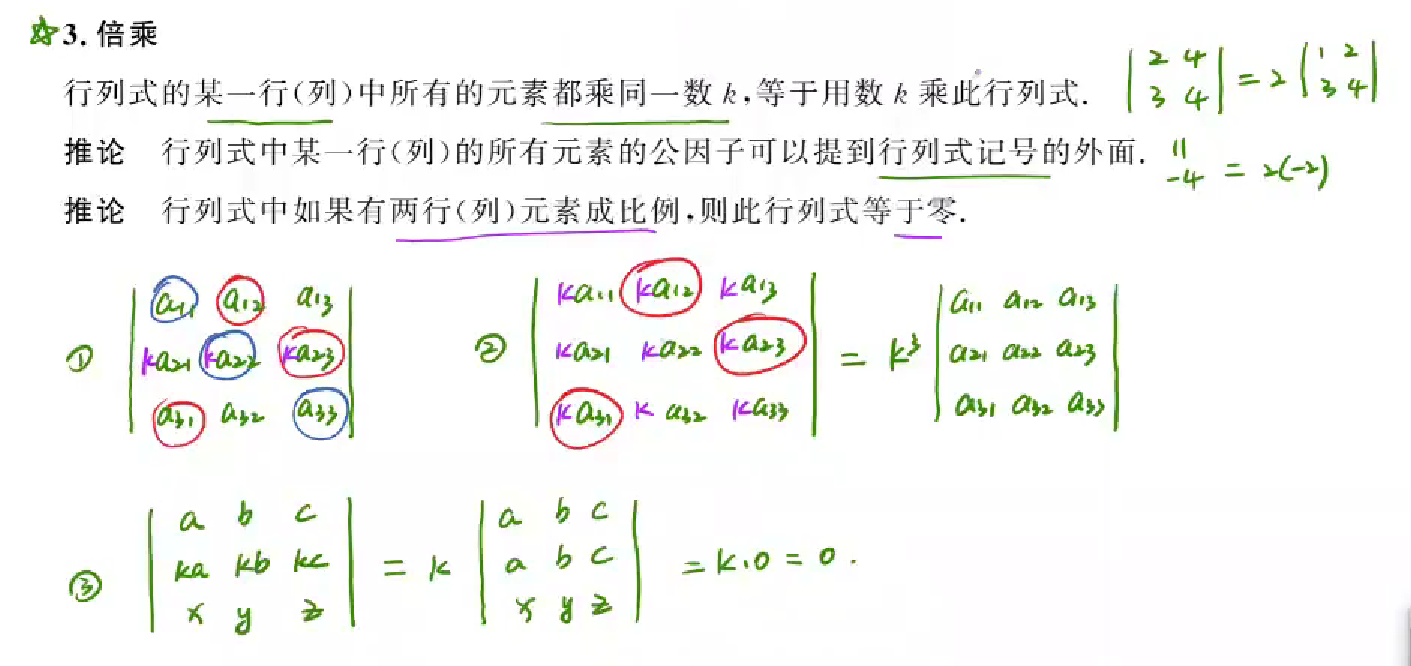
image.png

倍乘

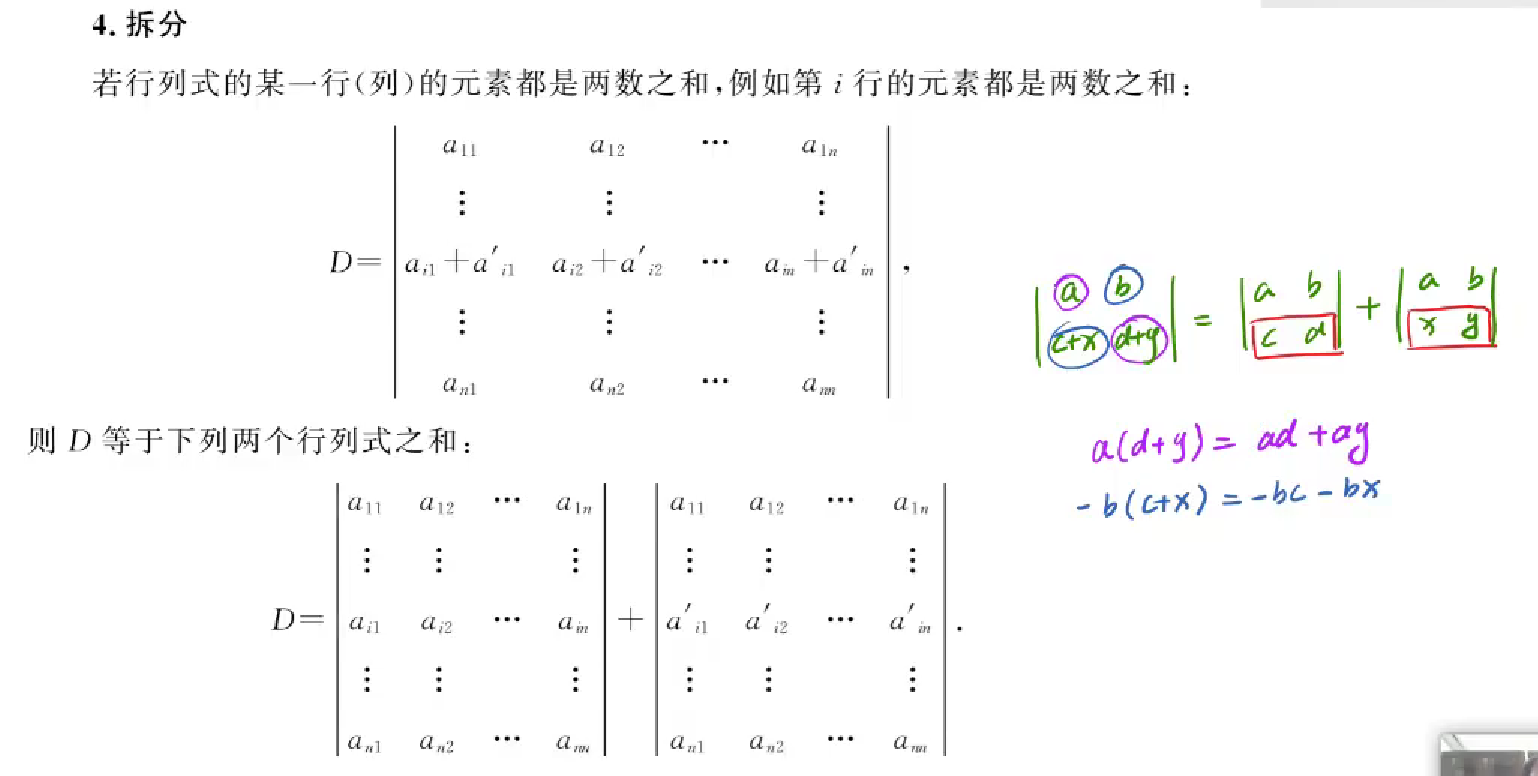
image.png

拆分

image.png

倍加

image.png
image.png

02-行列式的计算与代数余子式

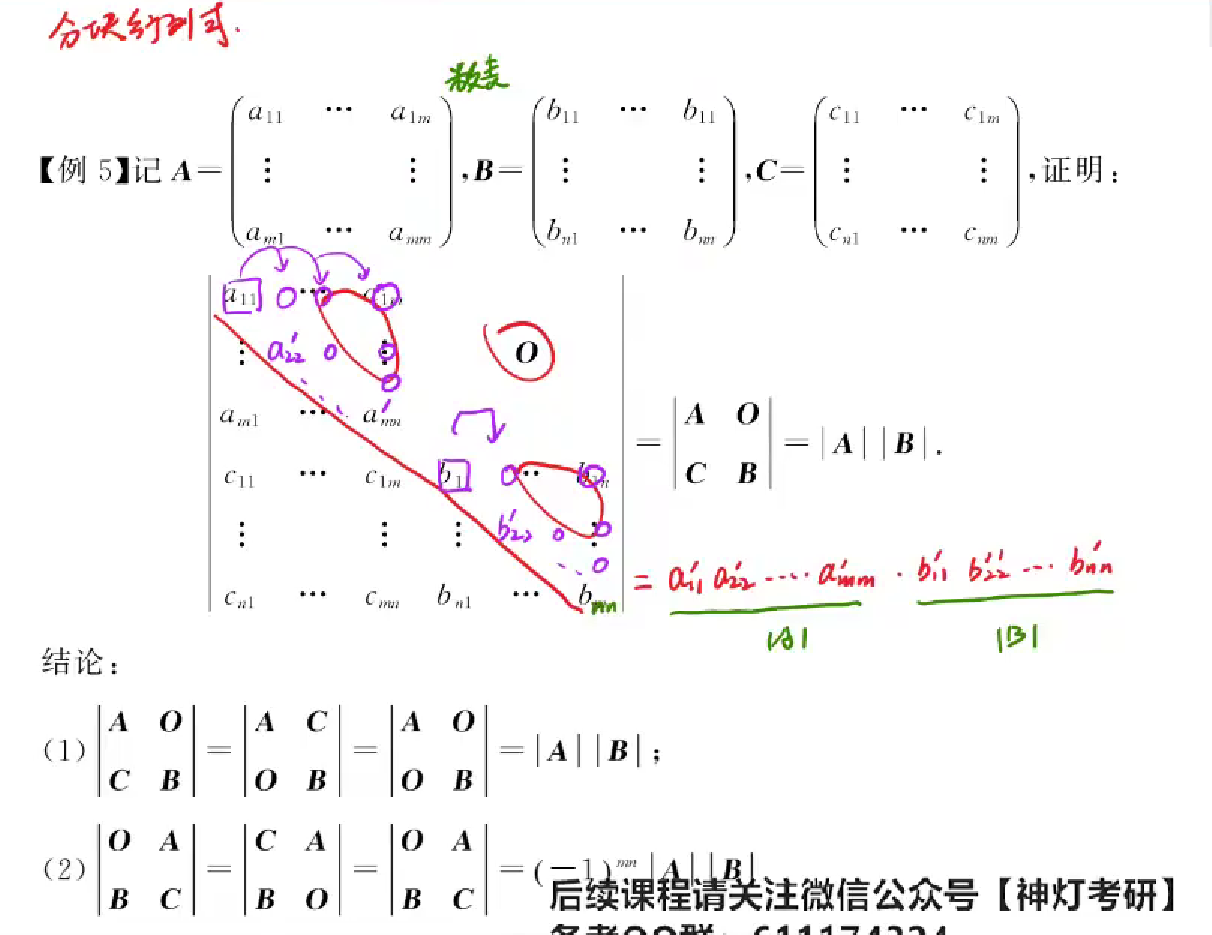
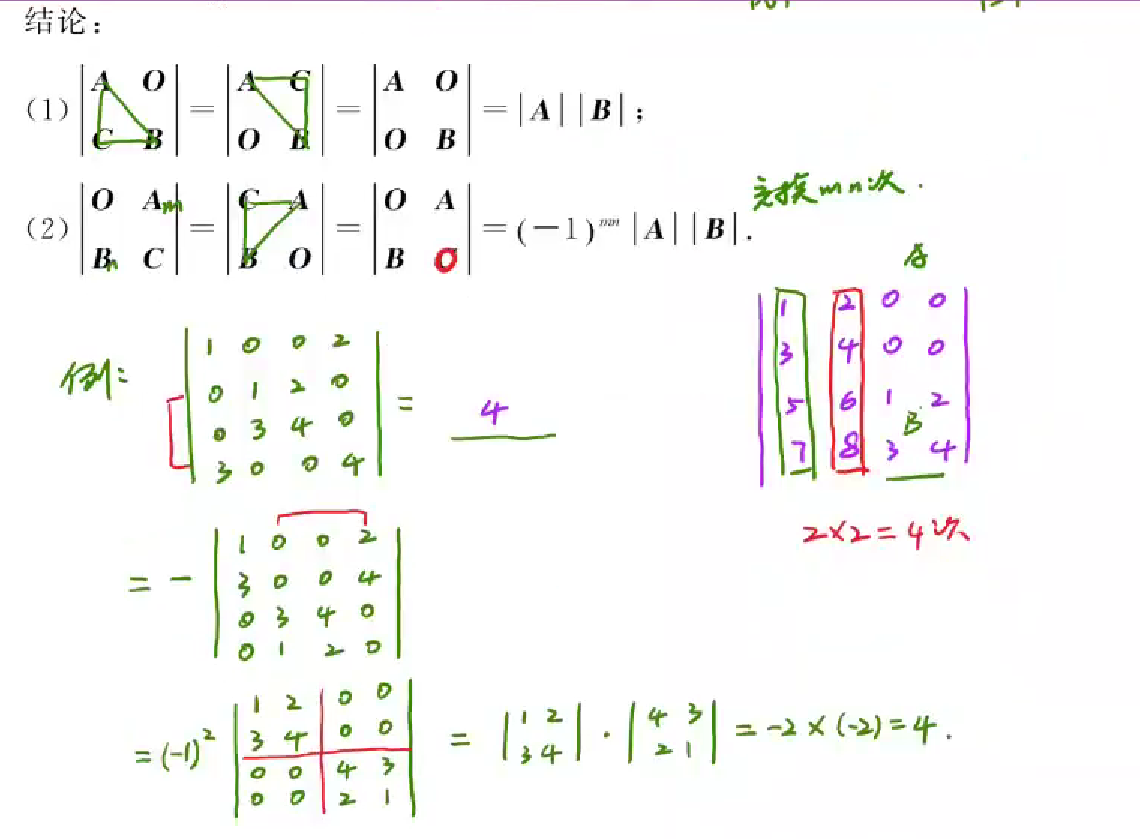
分块矩阵的行列式计算


image.png

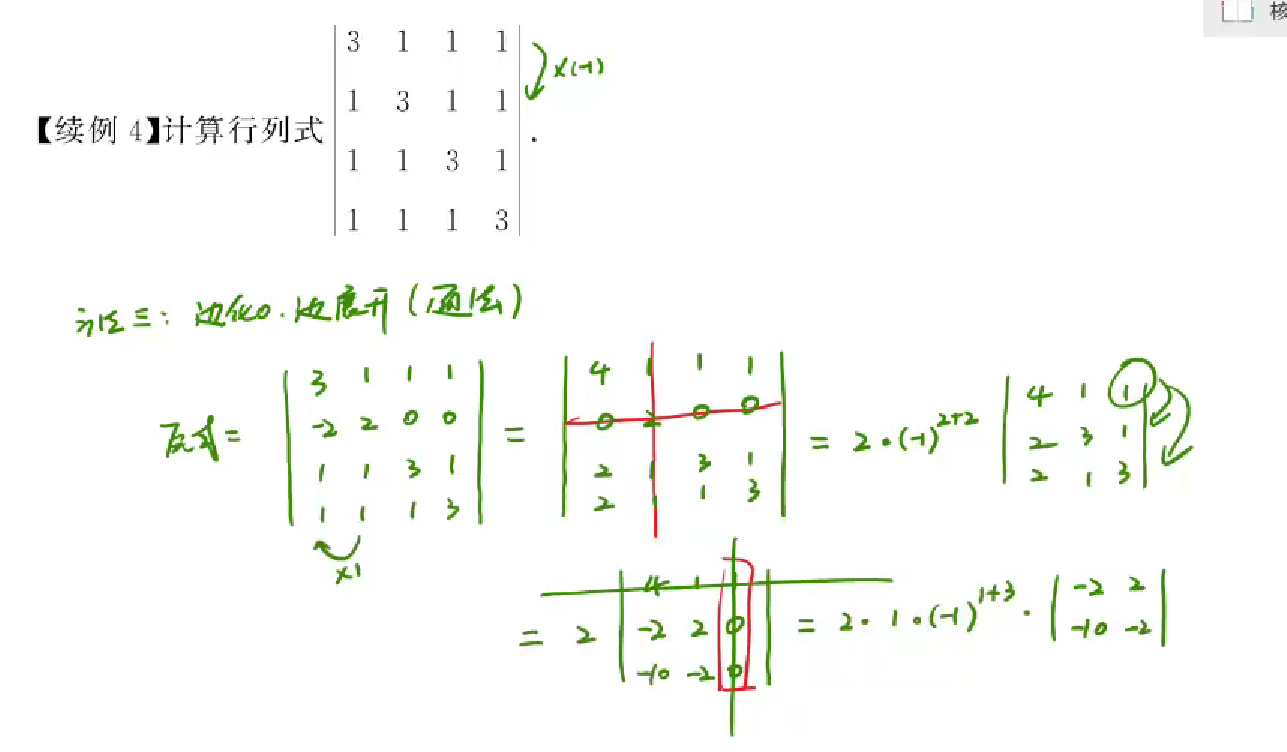
行列式按行(列)展开

展开定理

1
2
3
4
余子式M 是特殊的情况，恰好第一行第一个数不是0,该行其余都是0,行列式的值=a11xM11。
代数余子式A是讨论,不是特殊情况时，要考虑符号问题。
就是不断的交换将aij逐行逐列的移到第一个的位置(交换一次改变一次正负号),aij列需要j次
交换，行需要i次交换。所以符号-(1)^i+j x Mij = Aij

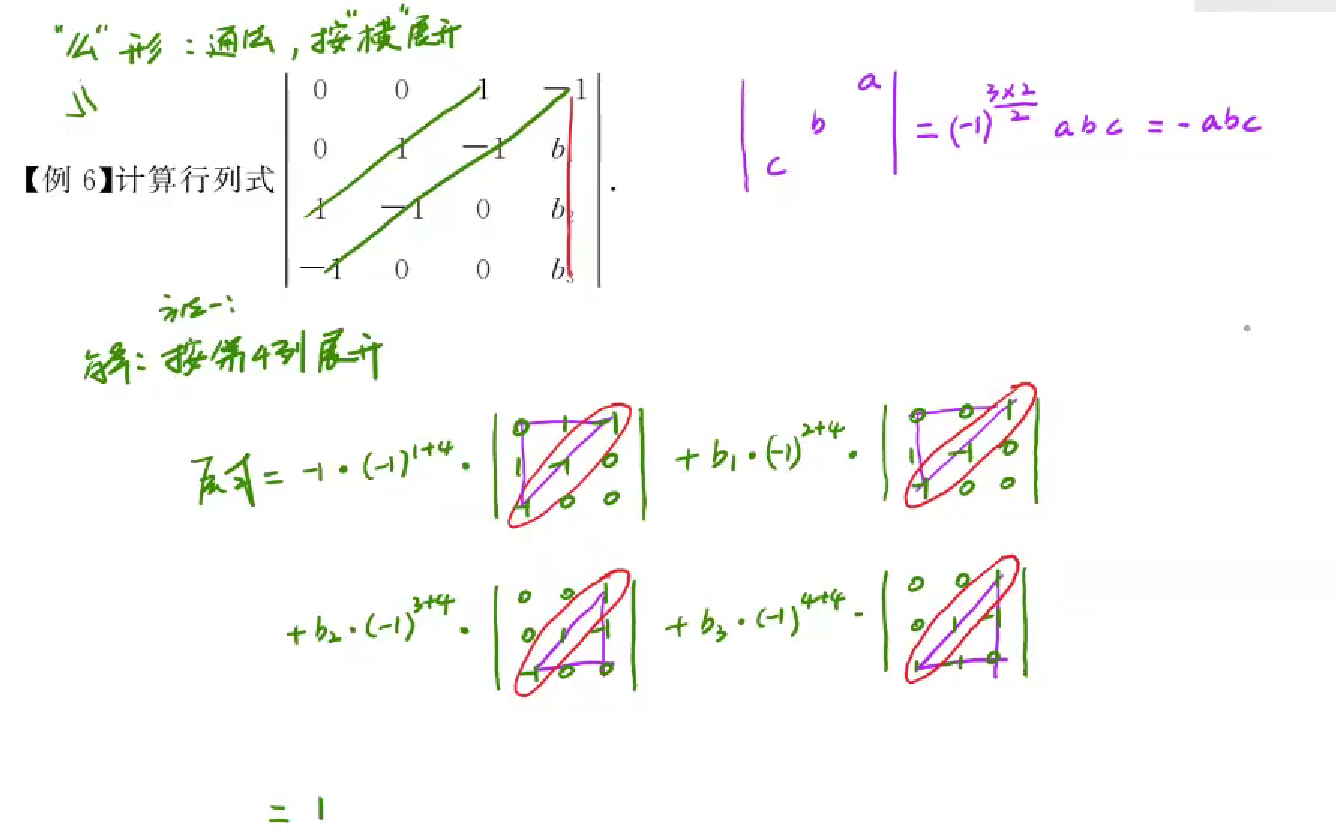
image.png

“么”型通法，按横展开

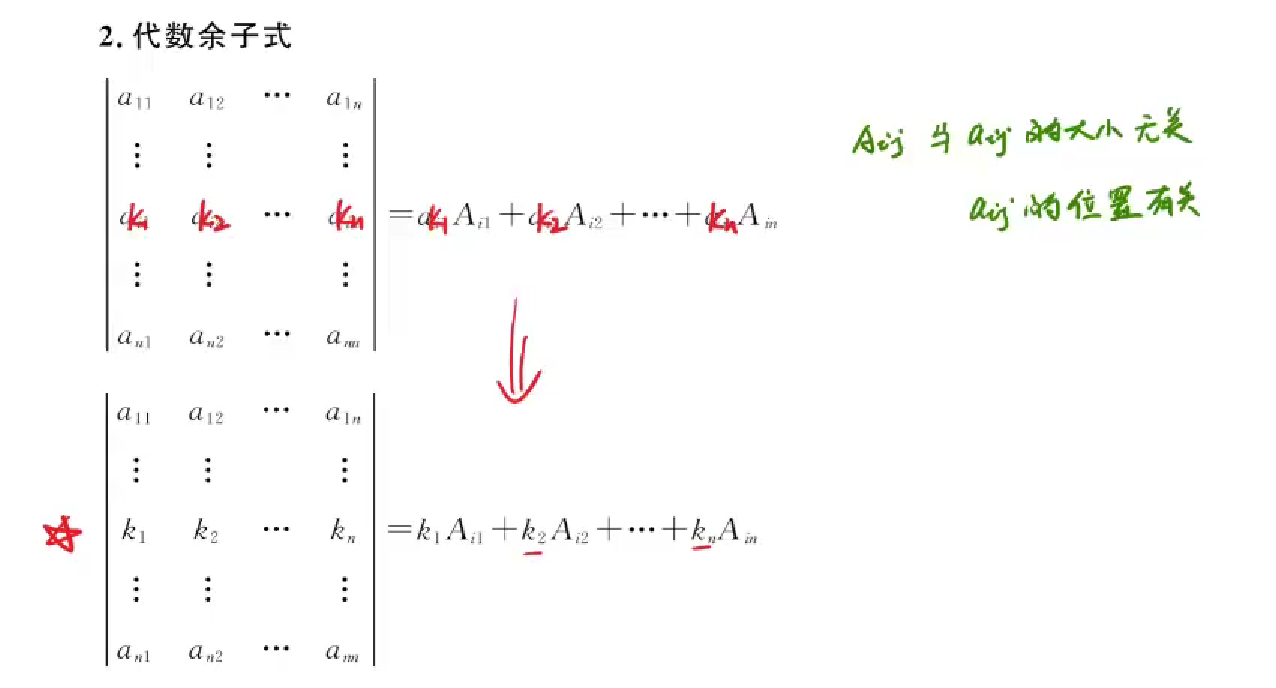
image.png

Uploading file...havyy

代数余子式

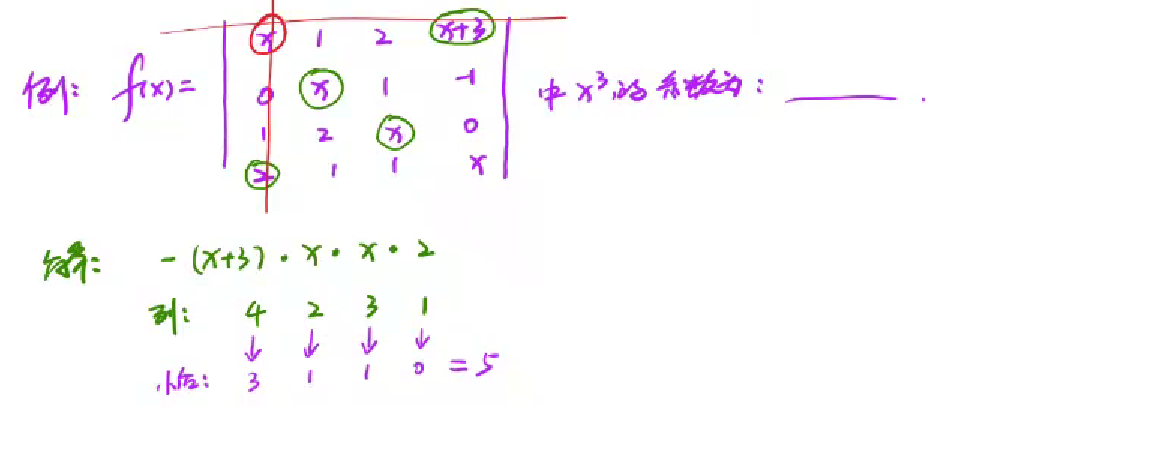
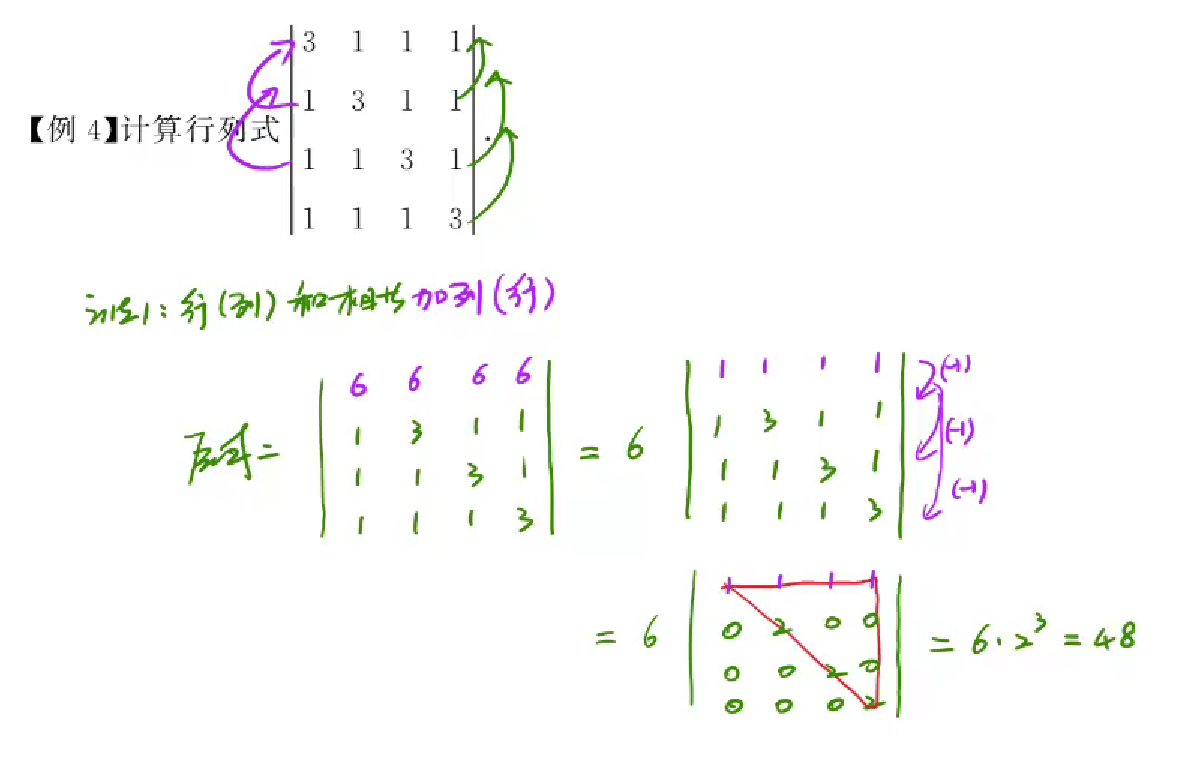
image.png

image.png

例题

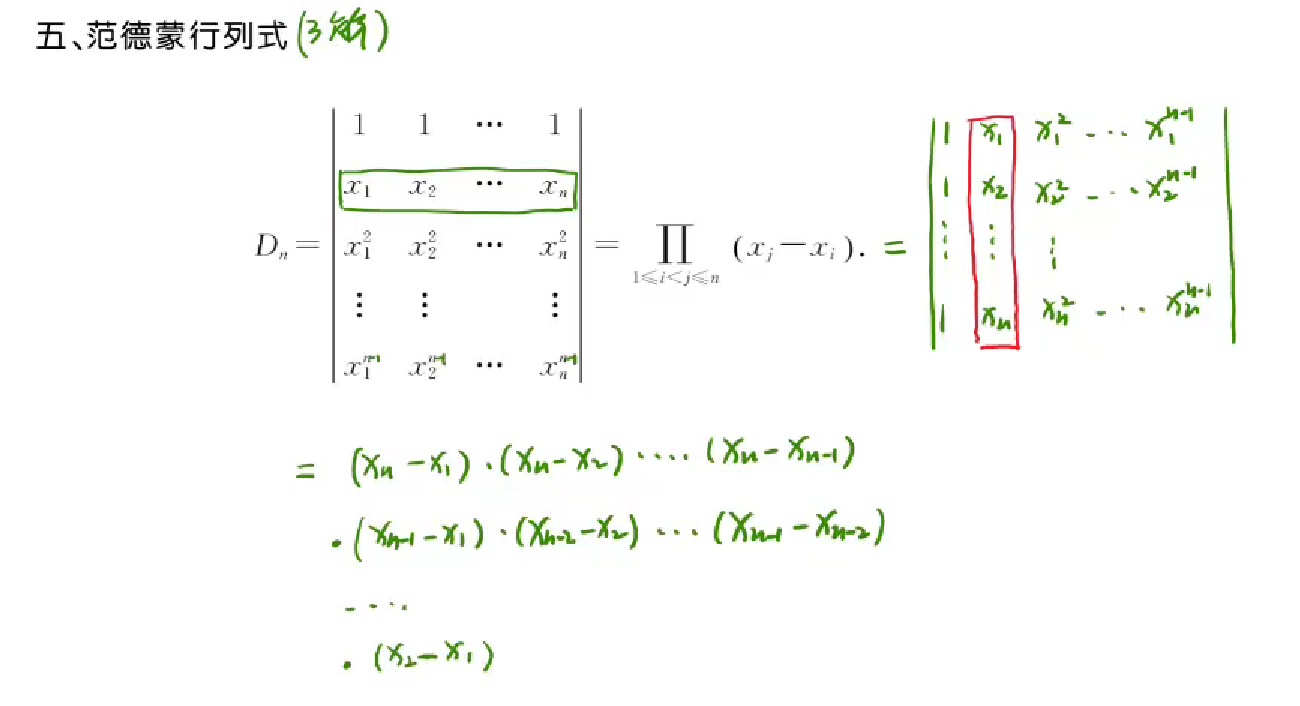
image.png
image.png
image.png

范德门行列式

1
2
像这种第一行(或列)是1，第二行(列)是x1,x2..xn;第三行(列)是x1^2,x2^2..xn^2;...第n行(列)是...
这种形式的就是范德蒙行列式，它的值有如下规律

image.png

1
2
方法1.加边法
	与范德蒙行列式相似的，可以加边使其成为范德蒙行列式

image.png

1
2
方法2.提公因子
	每一行提一个公因子，使得第一列的全为1，成为范德蒙行列式

image.png

03矩阵及其运算

矩阵及分块的概念

1
2
3
4
矩阵的提出主要源自于数学中的三个问题:
	1.线性变换:用于表示未知数的变换关系
	2.线性方程组:用于表示方程组各个未知数的系数
	3.二次型:方便表示二次型，x^2,y^2,xy,出现的个数

数表来源

image.png
image.png

特殊矩阵及分块矩阵

image.png

矩阵及分块矩阵的计算

加减法

1
2
3
矩阵加减法要求
1.同型矩阵，m,n相同
2.对应每个元素相加

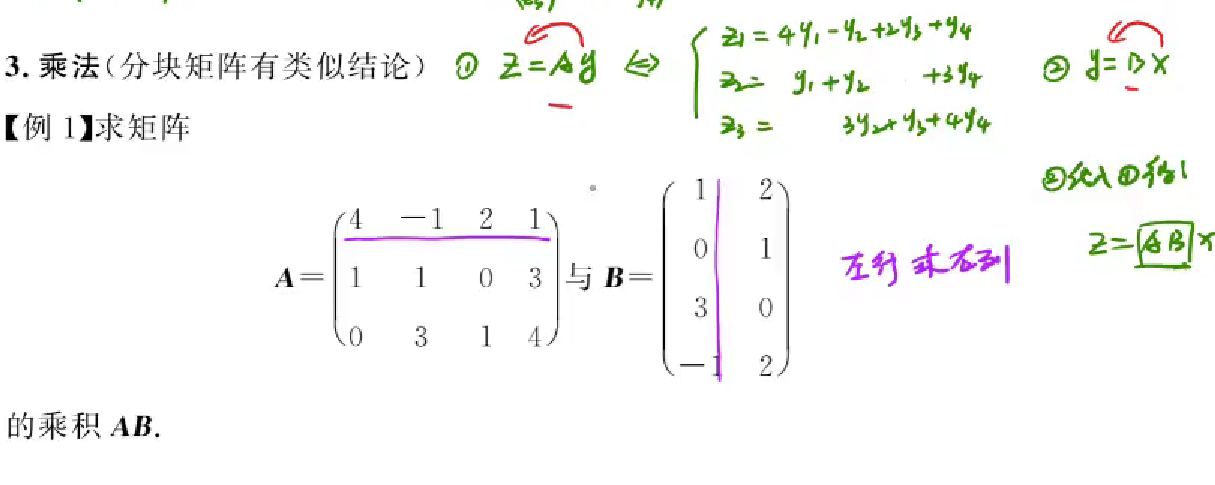
image.png

数乘

image.png

乘法

1
矩阵乘法，实质是将由x->y的线性变换通过y->z的变化 转到x->z的线性变换

image.png
image.png

对角矩阵的幂

image.png

坍缩矩阵的幂

image.png

坍缩矩阵练习

1
2
3
排列与组合区别在于，组合不要求内部顺序，所以要除以顺序个数

将A矩阵拆分为--> 单位E矩阵 + “坍缩矩阵”B

image.png
image.png
image.png

成比例矩阵的幂

1
2
3
每行成比例的矩阵，可以写为如下
成比例矩阵n次幂就可以拆为如下
...

image.png

与伴随矩阵相乘

1
2
3
4
5
6
7
8
9
10
AxA* --> 乘错行导致只有对应行的与其对应的代数余子式相乘结果才为|A|-->也就是只有对角线上是|A| 

为什么代数余子式，乘错行会=0？ 
因为,乘错行，可以看做求一个具有两行相元素的行列式的值-->两行相同元素的行列式=0

为什么两行相同元素的行列式值是0?
因为，利用交换一次行,矩阵正负性改变,两行相同交换后不变，但正负性改变，那么只能是0

为什么交换两行元素，矩阵正负性要改变?
因为，交换两行之后，导致每一项列排序发生一次交换-->逆序数奇偶性变化-->正负性改变

image.png
image.png

转置

image.png

方阵的行列式

image.png

image.png

逆矩阵

逆矩阵定义

image.png

逆矩阵充要条件

image.png

原矩阵行列式=0 =>伴随矩阵行列式=0

image.png

求二阶矩阵的逆矩阵方法

image.png

分块矩阵求逆矩阵

image.png

结论

image.png

应用

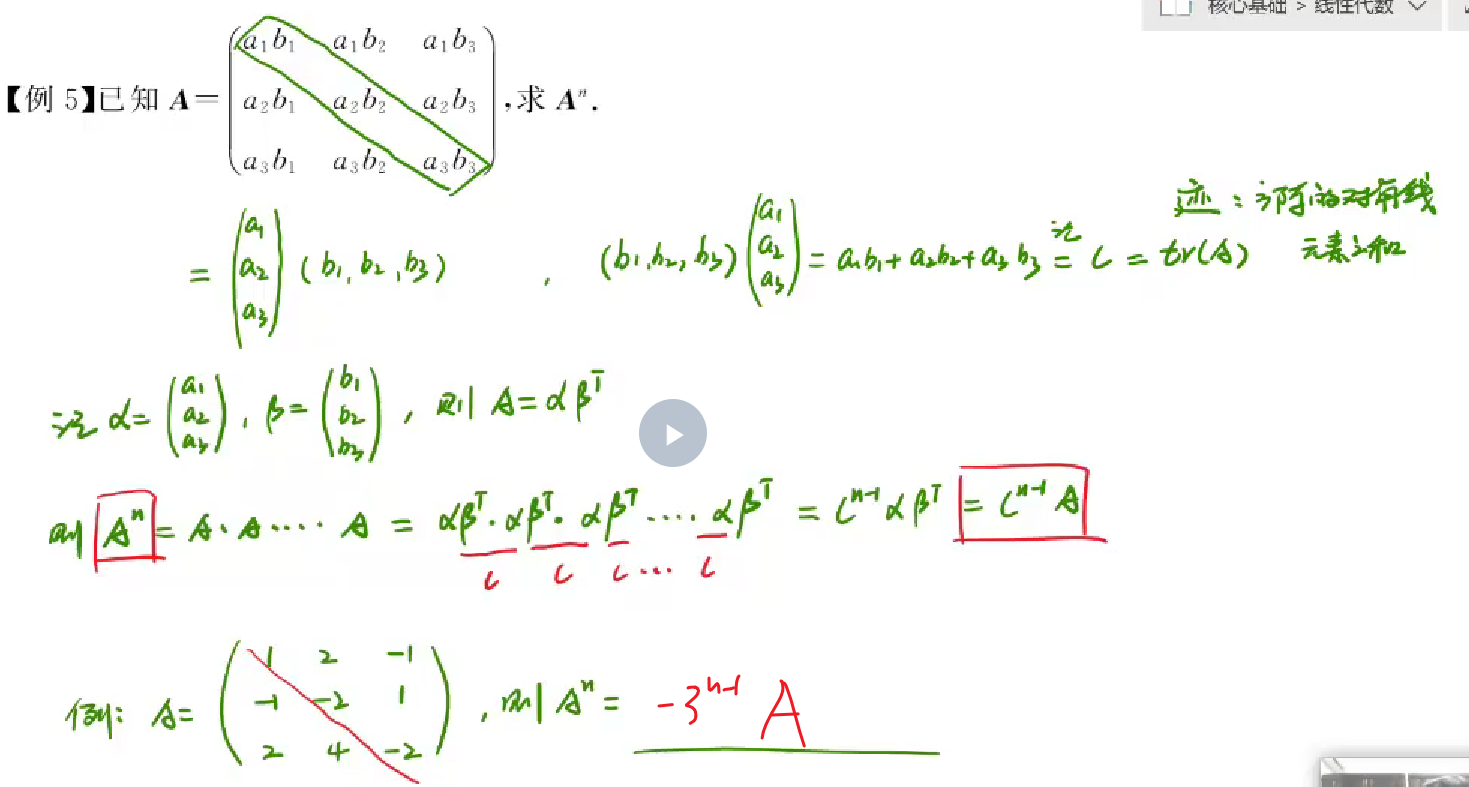
1
求可对角化的矩阵的幂-->先将矩阵写为下列形式，然后相乘，中间可以相互抵消为E(单位矩阵)

image.png

image.png

题型通法总结

image.png
image.png

image.png

04初等变换与初等矩阵

初等变换、矩阵的行阶梯、行最简、标准形

1
2
化为行阶梯型矩阵-->自上而下化简
化为最简型矩阵-->自下而上化简

image.png

1
2
3
4
5
矩阵A只进行行变换到B,称A与B 行等价
矩阵A只进行列变换到B,称A与B 列等价
如果即行又列，称A与B 等价 

不管行等价，列等价，等价 -->其秩都相等

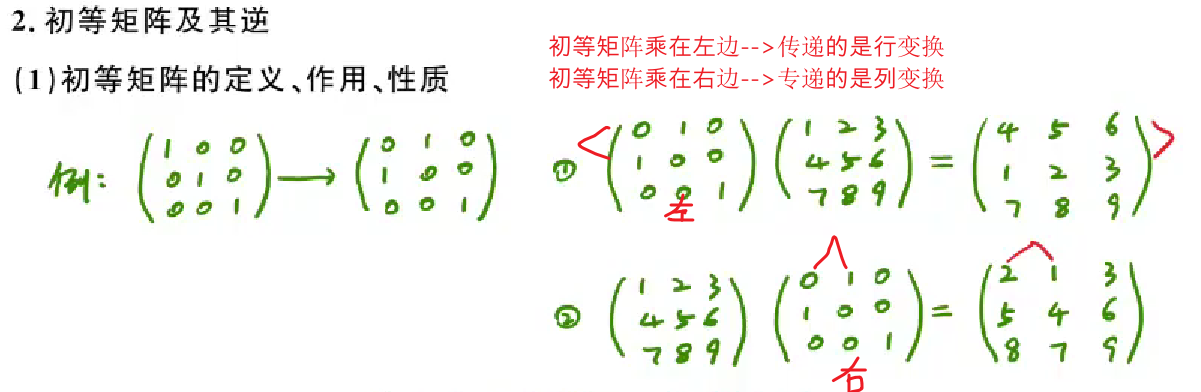
image.png

初等矩阵的定义性质

1
2
3
4
初等矩阵可以传递三种操作:
	1.交换: 左行右列 Eij -->交换第i、j行(列)
	2.倍乘: 左行右列 Ei(k) --> 第i行(列) 乘k倍
	3.倍加: 左行由列 Eij(k) --> (左)将第i行加上j行的k倍;(右)将第j列加上第i行的k倍

image.png

image.png

初等矩阵的逆

image.png

image.png
image.png

可逆矩阵都可初等变换化为单位阵

image.png

初等变换求逆矩阵-解可逆矩阵方程

image.png

1
2
1.A逆在左，行变换，所以可逆矩阵方程A,B要行摆放
2.A逆在右，列变换，所以可逆矩阵方程A,B要列摆放

image.png

image.png
image.png

05-矩阵的秩与线性方程组

秩

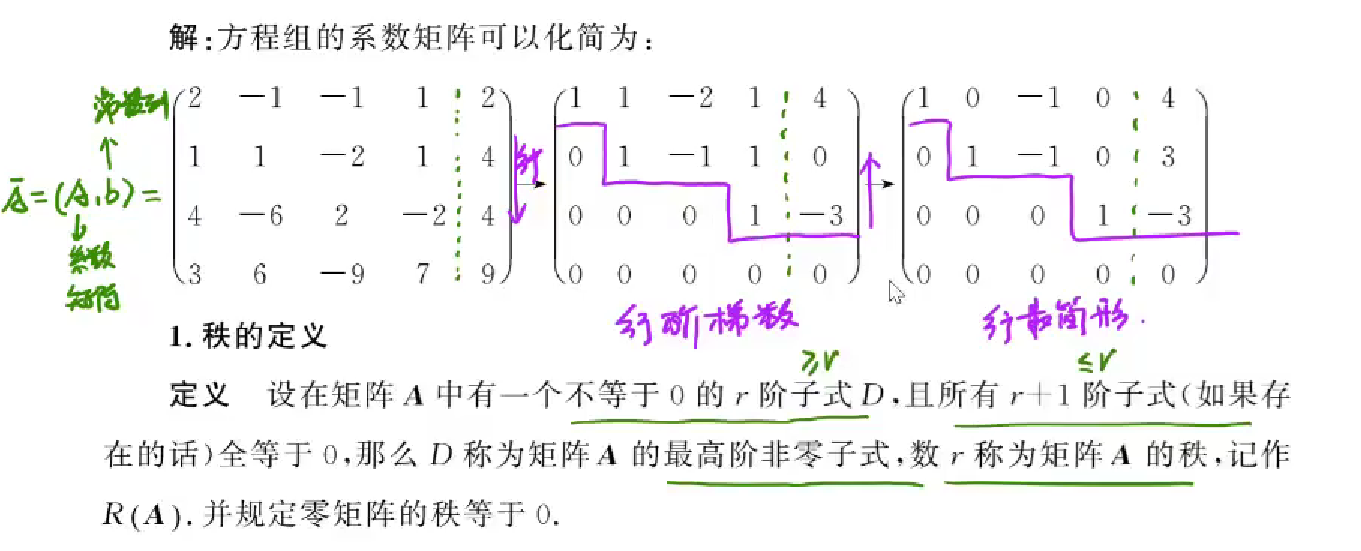
矩阵的秩的定义

1
初等变换不会改变秩的个数

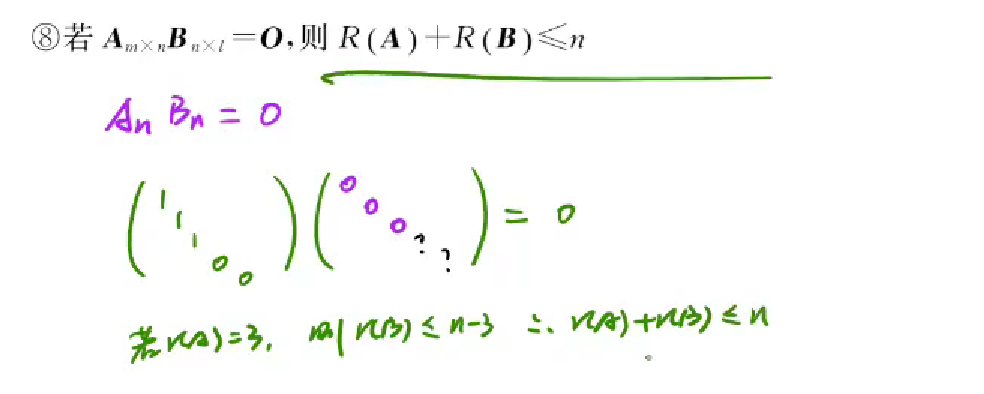
image.png
image.png

行阶形求秩

image.png

秩的结论

1
2
3
4
5
6
7
8
9
10
1.矩阵的秩不会超过行数也不会超过列数，因为逆矩阵的秩就是阶梯个数，阶梯怎么画都不会   超过行和列
2.转置矩阵的秩不变很好理解
3.等价的矩阵秩一定相等-->等价的矩阵实际就是在一个矩阵基础上经过若干初等变换得到的   两个矩阵，初等变换不会影响秩的大小
4.P,Q可逆-->P,Q是若干初等矩阵的乘积-->相当于对A经过若干初等行变换+列变换-->秩不变
5.(A,B)矩阵的秩R(A,B)min/max --> A,B都化为标准型之后，看斜对角线
6.矩阵相加的秩，化标准型理解
7.矩阵相乘的秩，化标准型理解(特殊:矩阵与其转置矩阵相乘，秩不变)
8.两矩阵相乘为0矩阵-->标准型中1刚好错开，那么R(A)+R(B)<=n
9.伴随矩阵的秩与原矩阵的秩的关系...
10....

image.png
image.png

image.png
image.png
image.png

1
10.R(Amxn) =n -->列满秩 ;所以A的标准型是上面E,下面O ; --> 标准型左边乘以可逆矩阵P(等效为若干初等变换) 得到A --> A标准型=PA ...

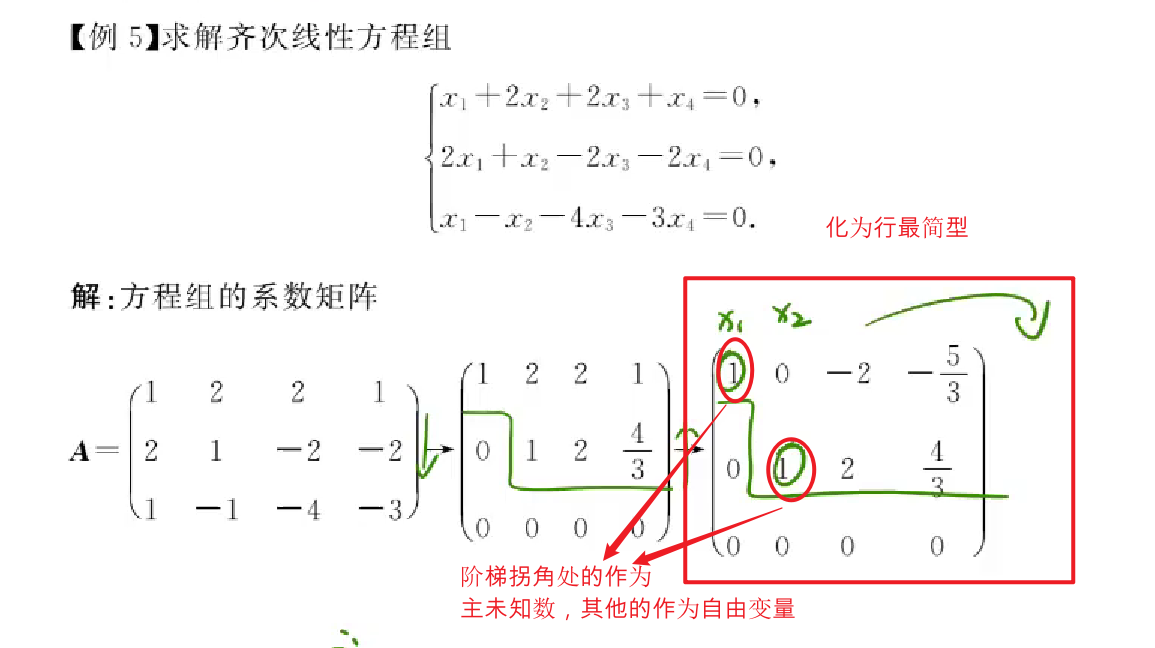
image.png

例题

image.png

线性方程组的解

解的判定

齐次线性

image.png

image.png

非齐次线性

image.png
image.png

具体方程组的求解

image.png
image.png

06-向量组的线性相关性

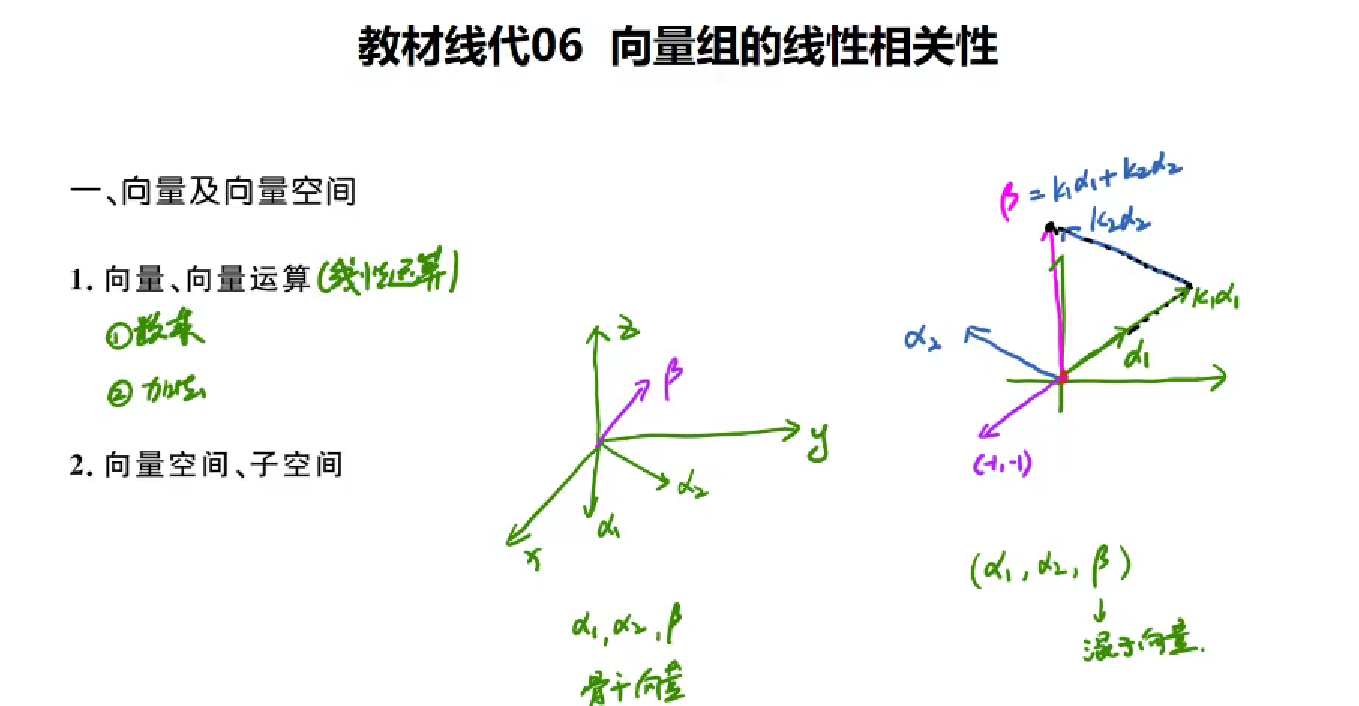
向量及向量空间

(a1，a2，β)向量组，其中如果三个向量共平面【其中一个向量，可以由另外两个向量通过线性运算：k1a1+k2a2 =β,得到，那么称为这组向量线性相关】
如果三个向量，不不再同一个平面，那么无法通过线性运算得到第三个向量，则线性无关

image.png

线性表示

线性表示

加入一个新的向量b，原矩阵的秩如果不变，说明向量b没有开拓新的维度
，就是可以用前面的向量线性表示出来，与其他向量线性相关，就是一个混子向量，没有作用
反之，若果秩增加，说明，是骨干向量，在几何上表现为翘了起来，开拓了新的维度，与之前的向量线性无关
image.png

image.png

向量组等价

两个向量组能够互相线性表示，那么这两个向量组等价
image.png

两个矩阵等价，只要求矩阵秩相等；
1.所以矩阵等价，推不出向量组等价，因为向量组1，和向量组2表示的平面不一定是同一个平面；
2.同理，向量组等价，推不出矩阵等价，因为向量组等价可以不同型，比如一个3列，一个2列，虽然向量组等价(多了一个混子向量)，但是矩阵不等价(矩阵等价需要同行同列)
image.png

例题
1.将两向量组和成一个，看维度是多少(秩是多少)
2.发现秩=2，且向量组1的秩也等于2，说明向量组2的加入没有增加维度，
3.继续看向量组2的秩=2，说明向量组1的加入没有增加2的维度
4.所以两个向量组可以互相线性表示，是等价的
image.png

推论

1.如果向量组A可由B线性表示，那么R(A)<=R(B)
反之不成立，因为如果R(A=1,一条线；R(B)=2,一个面，线不再面上，无法被B线性表示

线性相关性(齐次线性方程组有无非零解问题)

k不全为0，满足下列方程，那么可以互相消去，说明有混子向量，所以有非零解，线性相关的
k全为0，才满足下列等式，那么无法互相消去，全都是不重复的骨干向量，只有全0才成立
image.png

例题
image.png
image.png

推论
特别对于第二个结论：向量的维度，就是向量的坐标轴个数，一个三维向量，就是x,y,z坐标轴，最多三个骨干向量（分别表示x,y,z方向），再多一个都是混子，重复；同理四维向量，有4个坐标轴，最多四个骨干向量
image.png

向量组的极大无关组

就是向量组的骨干组，但凡多一个都是混子，所以极大无关组的向量个数也就是向量组的秩
image.png

线性方程组解的结构与判定

基础解系

  • 基础解系个数=自由变量的个数=未知数个数-主元的个数=n-r(A)
    image.png

解的结构

image.png

例题
image.png

向量空间

基于坐标

image.png

过渡矩阵

image.png

07-矩阵的特征值与特征向量

1.定义
设 A 是 n 阶矩阵，如果存在数 λ和n 维非零 列向量 α成立使 Aα=λα
那么称 λ为方阵A的一个特征值，α 称为 A 的对应于特征值λ的 特征向量.

  • 转化为求齐次方程有非零解的问题，系数方程是λE-A，解向量是α
  • 有非零解–>系数矩阵秩<n,所以矩阵的行列式=0
    image.png

例题

image.png
image.png

2.性质

  • 特征值的和=矩阵对角线系数的和
  • 特征值的积=矩阵行列式的值
  • 不同特征值对应的特征向量线性无关
  • n重根的特征值对应的线性无关的特征向量,最多n个
    image.png
    image.png

3.与A相关的矩阵的特征值与特征向量

image.png
image.png
image.png

例题
image.png

08-相似矩阵与相似对角化

相似矩阵

1.定义
两矩阵相似，可以推出以下5个推论
image.png

image.png

2.性质

  • 相似矩阵特征值相同，但是特征值相同的矩阵不一定相似
  • 相似矩阵秩相等(利用初等变换理解)，但是秩相等的不一定相似
    image.png

相似对角化

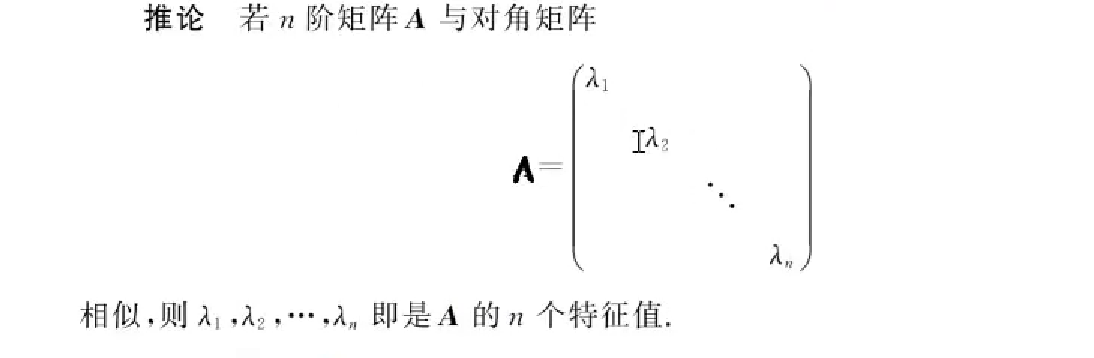
  • 若n阶矩阵A与对角矩阵相似，pAp^-1 = ∧ ，那么对角线上的n个值就是A的n个特征值

  • 证明如下：矩阵A一定能写成Aα=λα，那么A(α1,α2,α3)=(Aα1,Aα2,Aα3)=(λ1α1,λ2α2,λ3α3) ; 假设P=(α1,α2,α3)且可逆，那么AP=P∧ ，这个对角矩阵∧对角线上的值就是特征值
    image.png
    image.png

  • 判断一个矩阵可不可以对角化，就是看他的特征向量组成的矩阵是不是线性无关的–>可逆的

  • 因为矩阵|A|=特征值相乘–>那么将A进行初等变换不改变矩阵行列式的值–>对角化相当于对A进行初等变换，行列式的值不变，那么得到pAp^-1 = ∧，
    |∧|=特征值相乘，所以对角线上就是特征值；进而可知，这个P矩阵就是特征向量矩阵（α1，α2，α3），如果这个P矩阵可逆，就说明相似矩阵∧(对角矩阵）存在，那么就是可对角化；如果P不可逆，说明pAp^-1 = ∧不成立，A 与
    ∧不相似，就是不可对角化。

  • 所以，需要证明一个矩阵A可不可以对角化
    1.就是要先求出所有特征值。
    2.分为三种情况讨论：
    (1). λ1 != λ2 != λ3,分别所对应的特征向量α1，α2，α3)线性无关，P=（α1，α2，α3）一定可逆，所以A与∧相似，可对角化；
    (2) λ1 = λ2 != λ3，可以确定α2，α3线性无关，接着判定α1，α2是否线性无关即可，如果不是线性无关,那么P就不可逆，相似不成立；
    (3) λ1 = λ2 = λ3，….

image.png

  • 定理
    image.png

例题1

  • 计算特征值，可以展开某一行，也可以直接算，然后通过多项式除法化为因式相乘
  • 代入特征值，解齐次线性方程得出对应特征向量
  • 注意P向量中特征向量与对角矩阵中特征值的位置顺序要对应
  • 令P=(α2，-α1，2α3) ,A的对角矩阵中对角线上的特征值还是原来，只是换了位置，【λ是替代的A,与特征向量倍数无关】
    image.png
    image.png
    image.png
    image.png

例题2
image.png

结论1

  • n阶方阵A的秩<n,则A一定有特征值=0，|A||α|=λ|α|
    image.png

09-对称矩阵的对角化

1.对称矩阵的性质

  • 对称矩阵特征值一定是实数
  • 对称矩阵两个不同特征值对应的特征向量是正交的
  • 对称矩阵一定可以对角化
  • 对称矩阵，一定有正交矩阵可以与其相似对角化和合同对角化
    image.png
    image.png

例题1
1.对称矩阵，且三个特征值互不相等，所以三特征向量正交，互相内积为0
image.png

例题2
image.png

2.正交矩阵与合同对角化

正交矩阵
与自己的转置矩阵相乘=单位矩阵的矩阵，称为正交矩阵，顾名思义，正交矩阵，里面的向量两两正交；另外需要满足，正交矩阵的向量都是单位向量**
image.png

合同的定义
image.png

合同对角化的步骤

一般只讨论对称矩阵的合同对角化

  1. 将对称矩阵合同对角化，就是求出P矩阵，可使得P^TAP=∧；
  2. 要求出P，由于讨论的是对称矩阵A，所以就是求可以使得A相似对角化的可逆矩阵P，同时必须满足P是正交矩阵
  3. 所以步骤依旧是：求出特征值，分别算出特征向量
    • 当λ1 != λ2 != λ3，则对于对称矩阵，特征向量一定两两正交
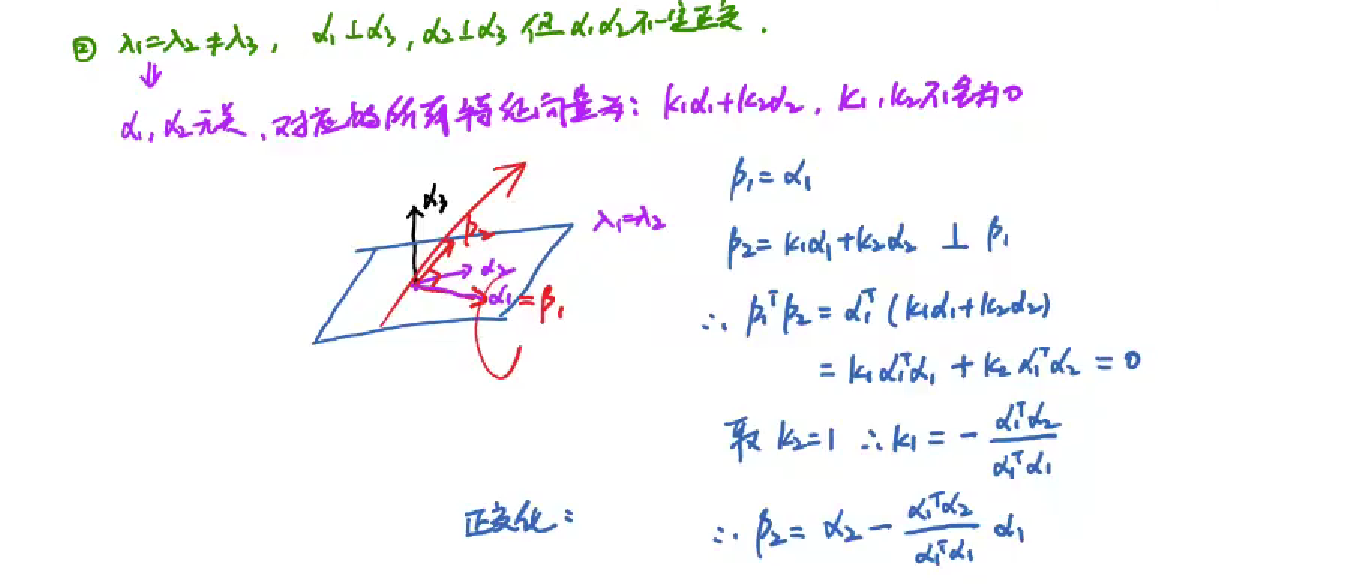
    • 当λ1 = λ2 != λ3，α1、α2都与α3正交，但α1与α2不正交。这时需要假定其中一个不动，再平面上组合取一个与其正交的特征向量即可【只有同一个特征值对应的几个特征向量才能互相组合，组合后还是特征向量】
    • 当λ1 = λ2 = λ3，不会考这种
      image.png
      image.png

例题1
单位化和正交化
image.png
image.png
image.png

10-二次型及其标准型

二次型及其系数矩阵

  • 系数矩阵要求是对称矩阵
    image.png

正交变换化二次型为标准型

  • 二次型的系数矩阵是对称矩阵，二次型的标准型是只有平方项，也就是说，标准型是对角矩阵
  • 要化系数矩阵A为标准型的矩阵∧，就是进行对角化
  • 这种题目一般是要求一个正交变换，使得系数矩阵能够化为标准型
  • *首先要知道，任何一个二次型,都可以用矩阵方式表示X^T A X *
  • 正交变换，是指存在一个正交矩阵P,进行x=Py的线性变化使得系数矩阵化为标准型
  • 要求这个正交变换，实质就是进行相似对角化，求特征值，得出特征向量，写出P,正交化，单位化，这个P就是正交变换
  • image.png

image.png

配方法化二次型为标准型

配出来的P矩阵要验证是否可逆，不需要P是单位阵，也不需要是正交矩阵，只需要可逆即可，因为这没有利用相似化做
image.png
image.png

例题1

image.png

例题2
image.png
image.png

规范型

规范型，就是标准型，系数都为1，只保留符号正负
由于标准型系数五花八门，标准不统一，所以化为规范型，好阅卷
image.png

二次型的正定性

判断一个对称矩阵是否正定：

  1. 正交变换法化为标准型，看得到标准型矩阵，对角线的特征值是否都>0
  2. 配方法化标准型，看得到的标准型矩阵，对角线的数是否都>0
  3. 看正惯性指数，看是否全都是正的
  4. 看A的各阶主子式是否都为正
    判断一个对称矩阵是否负定：
  5. 前三条与上面正好相反
  6. 看A的各阶主子式，奇数阶为负，偶数阶为正，那么就是负定
    image.png

image.png
image.png

例题1
image.png