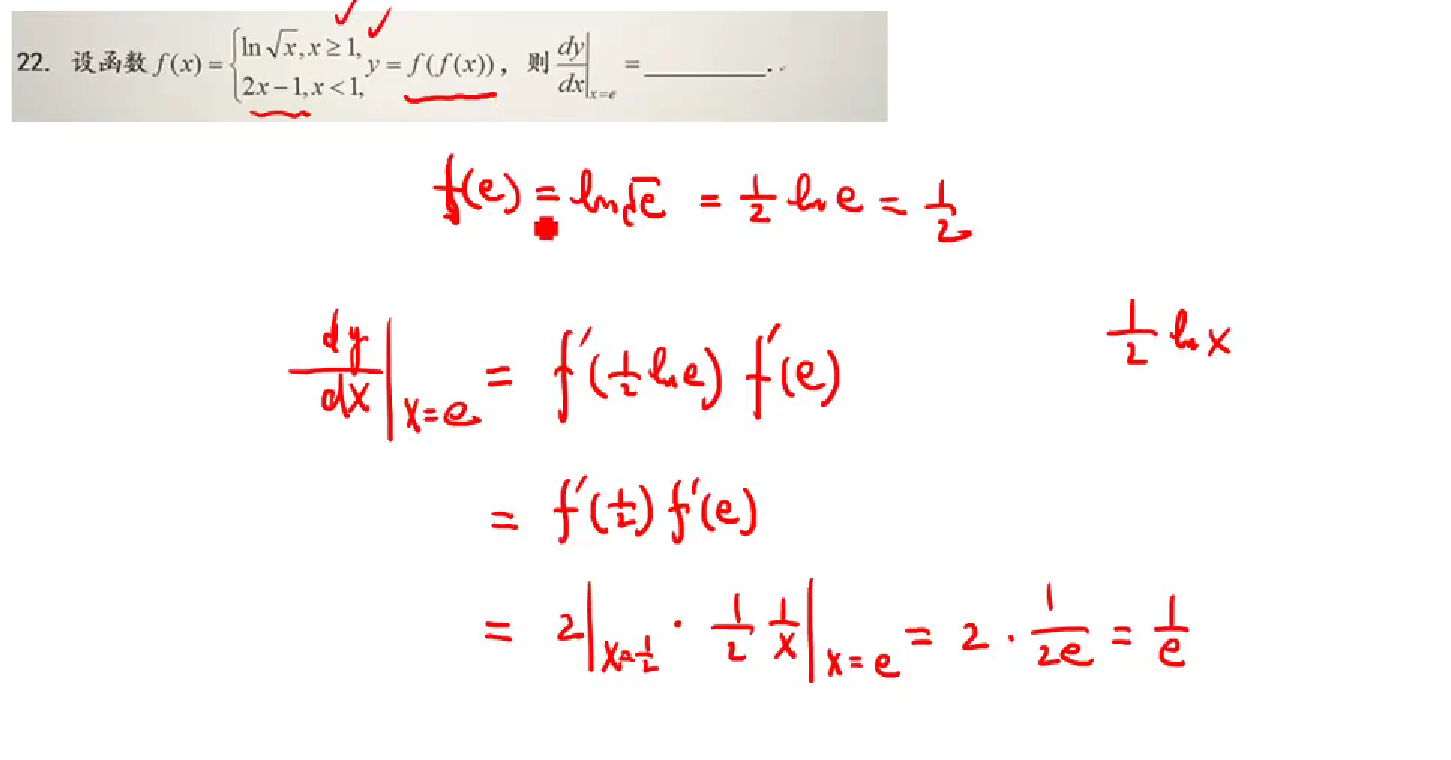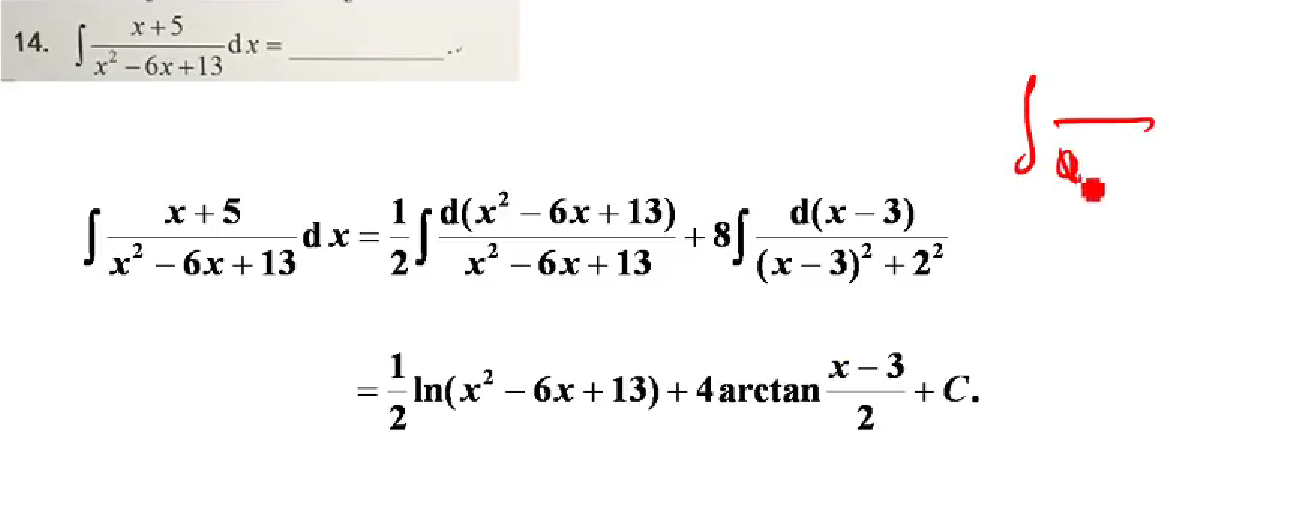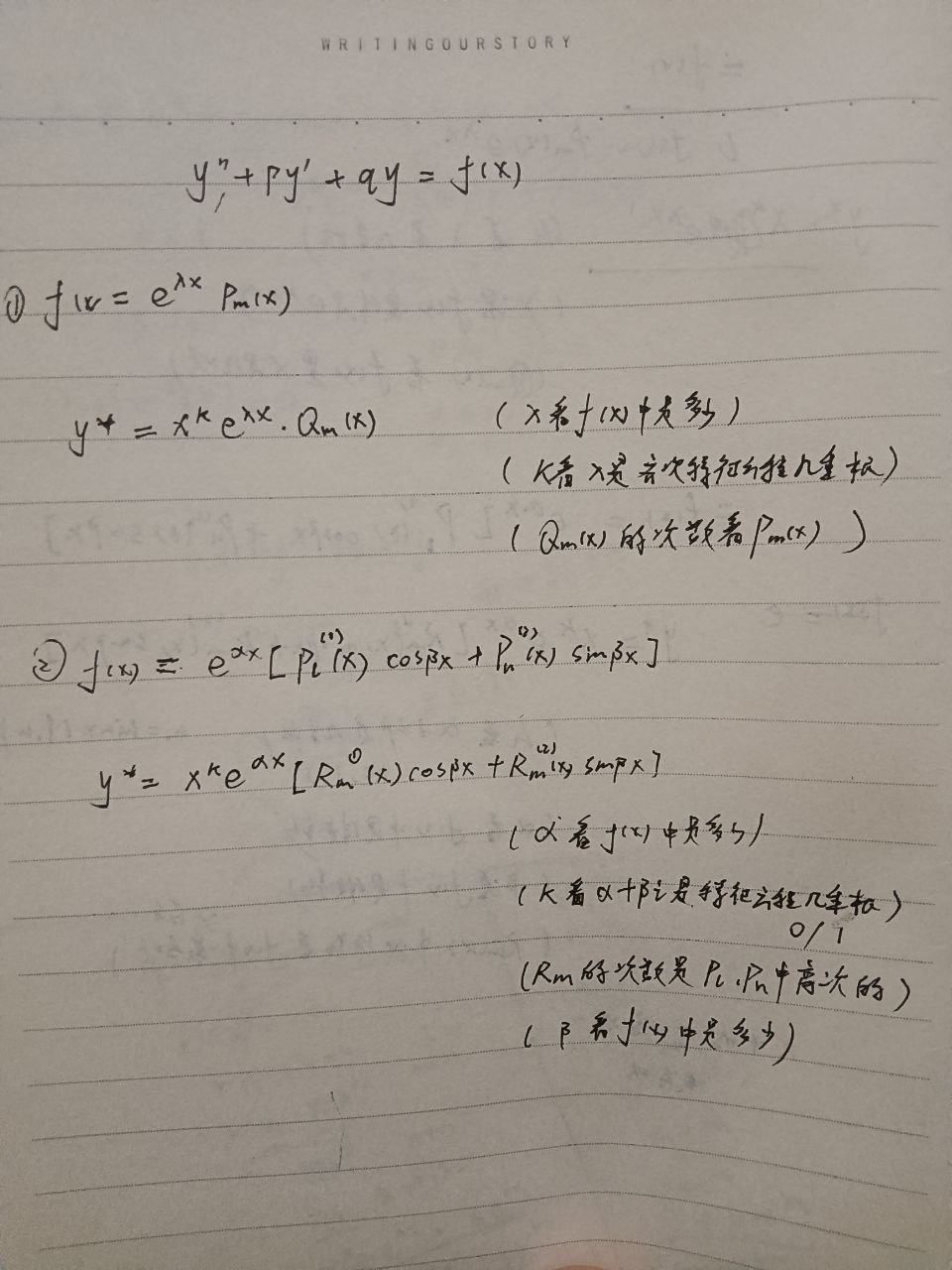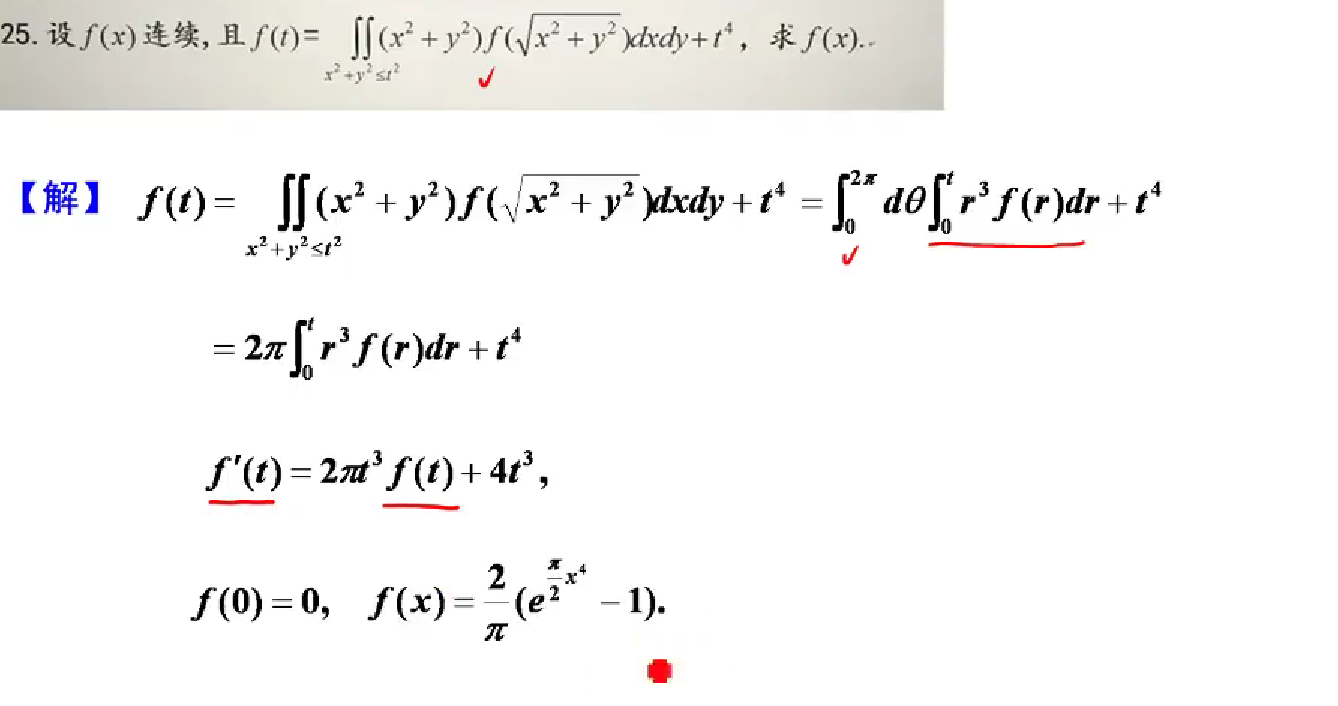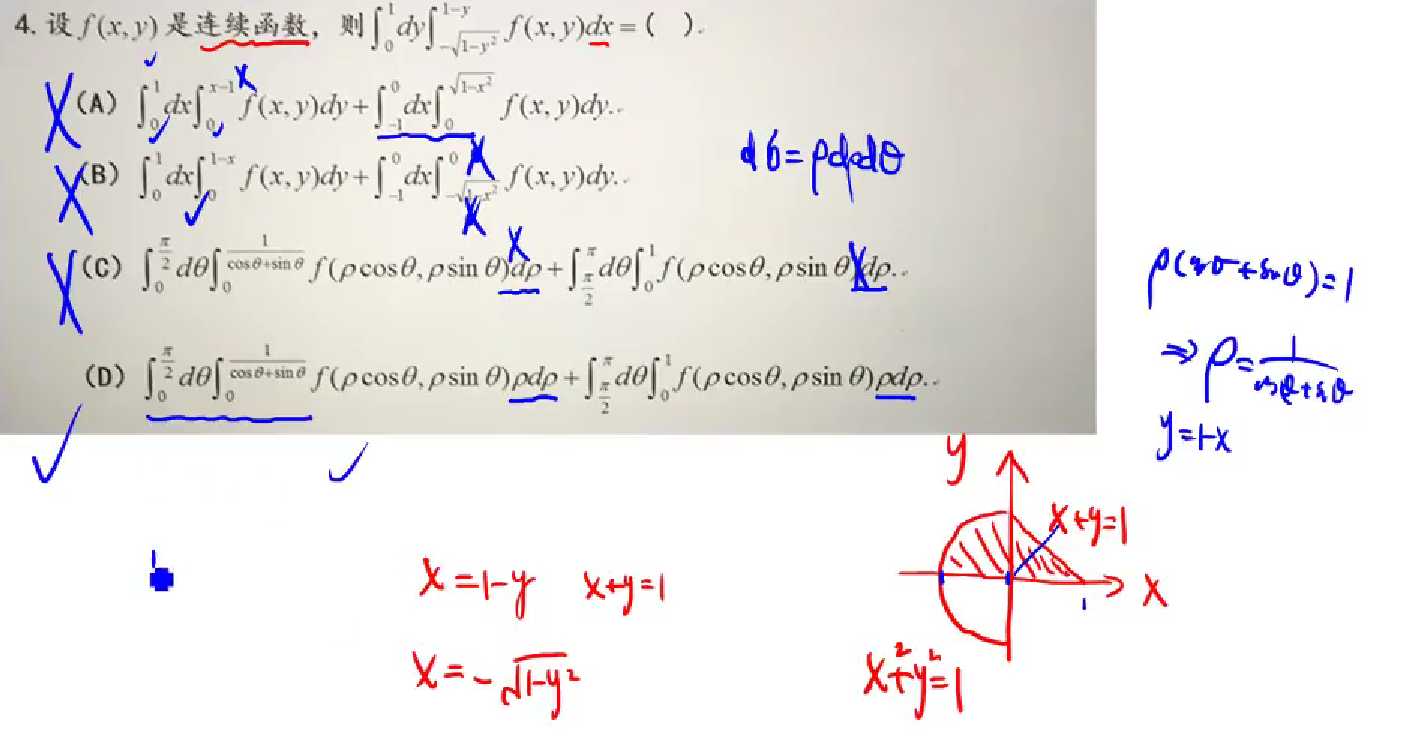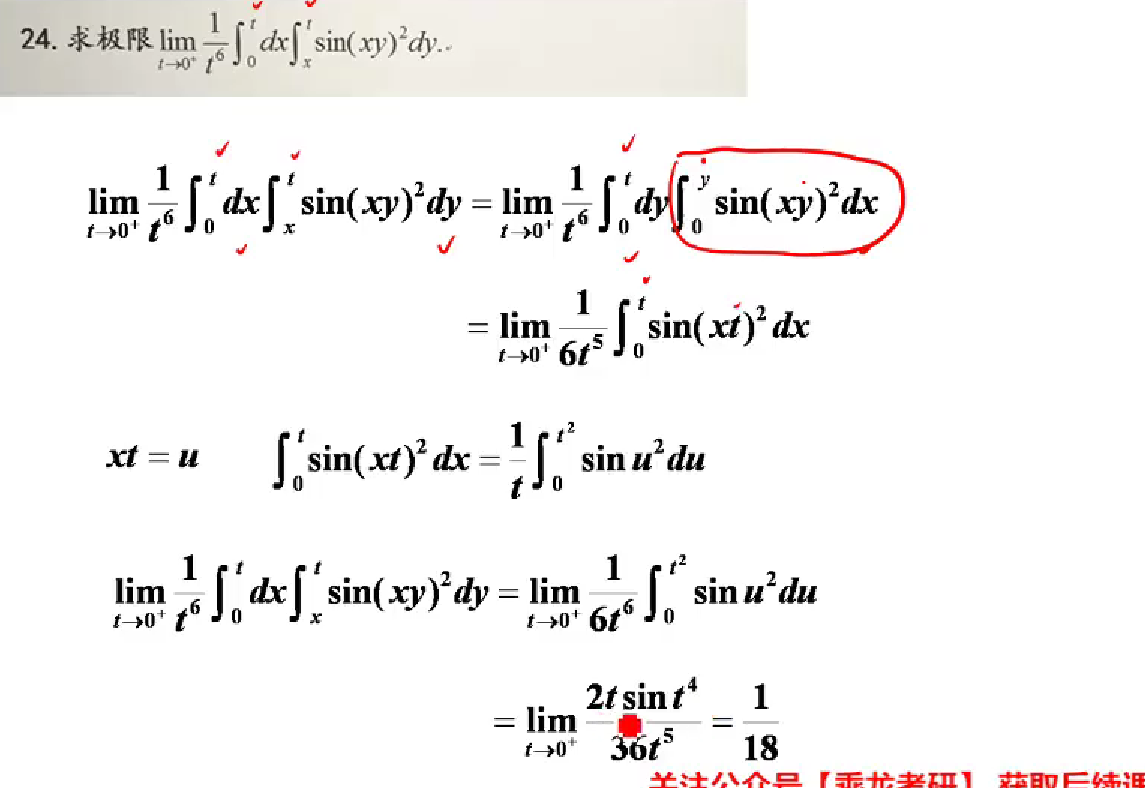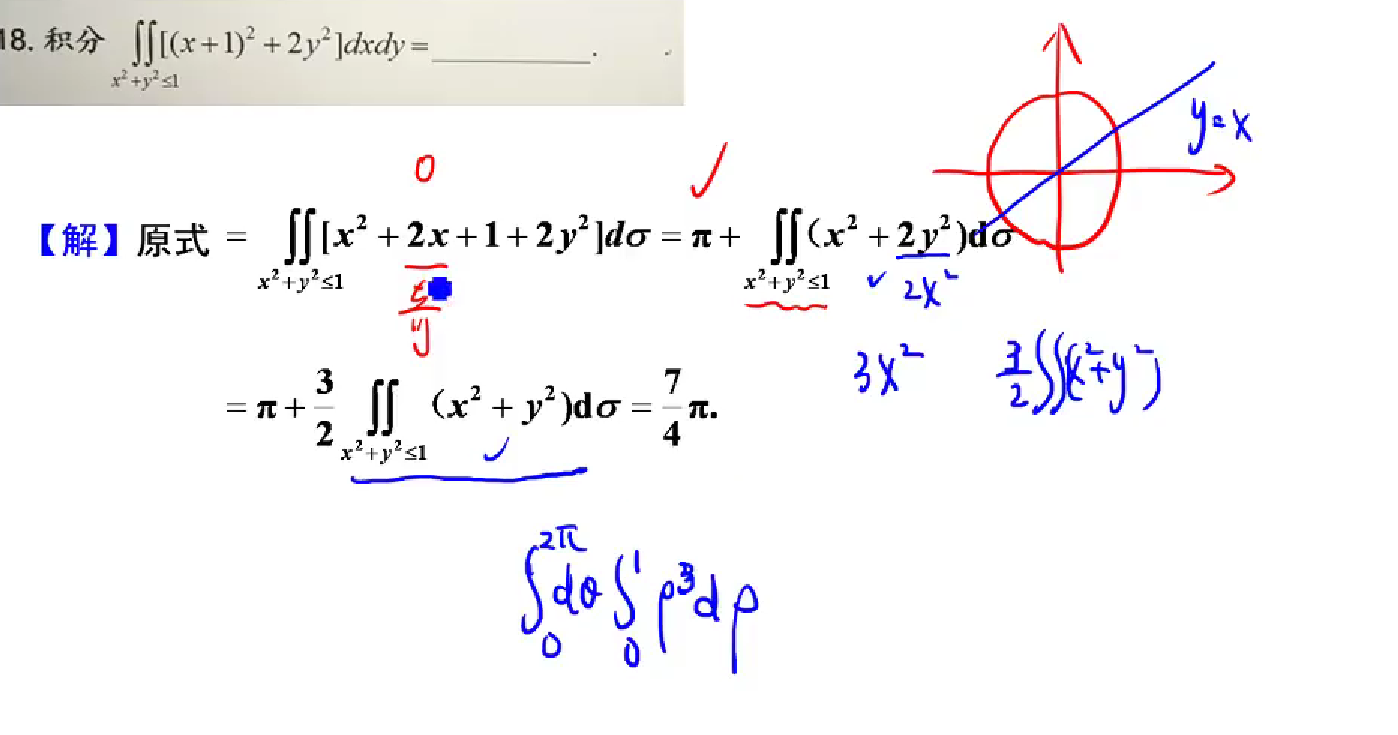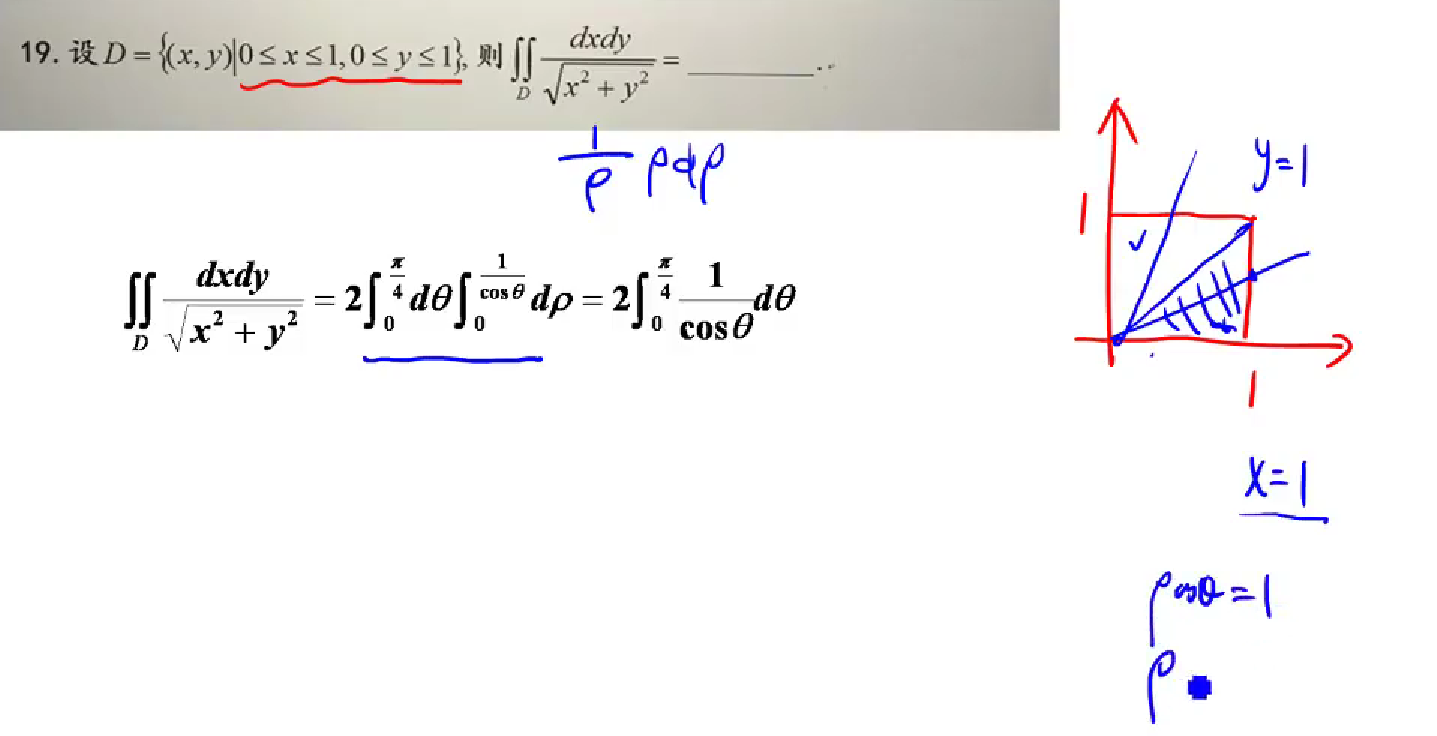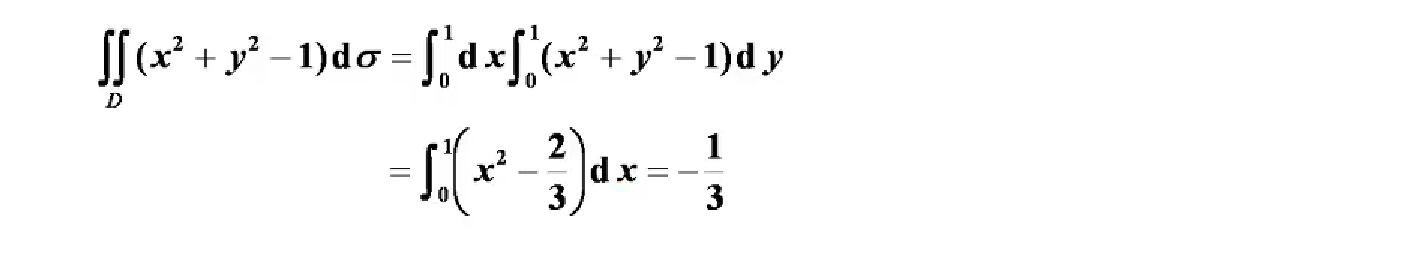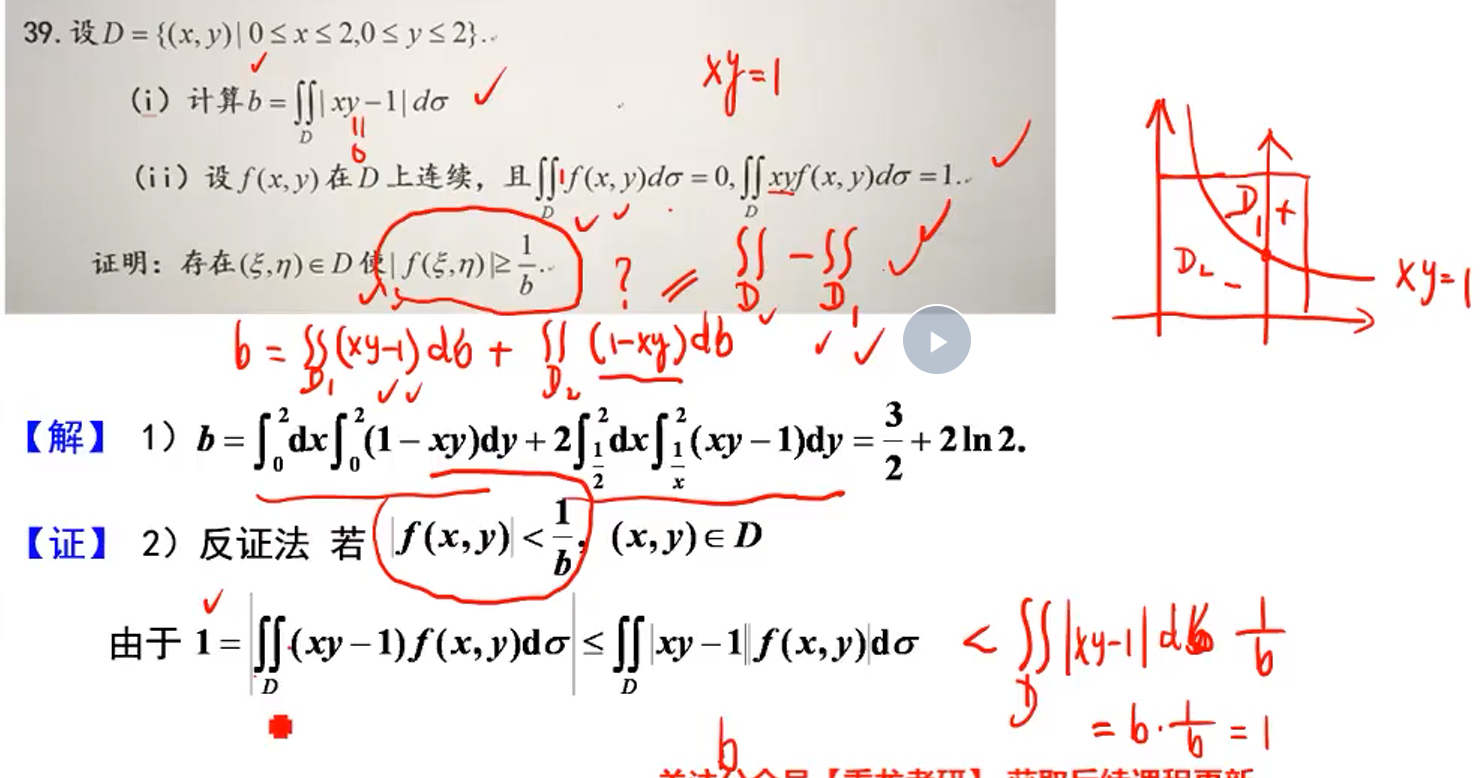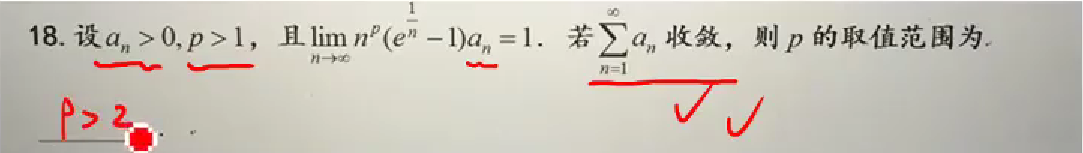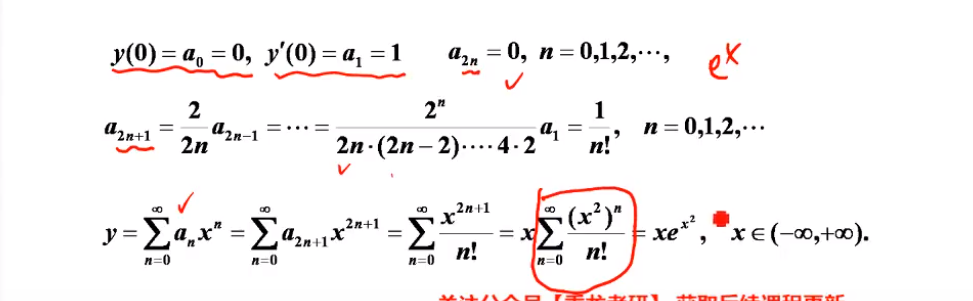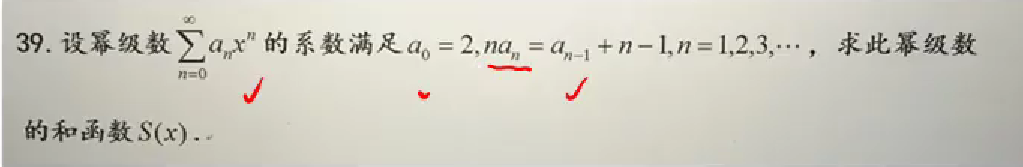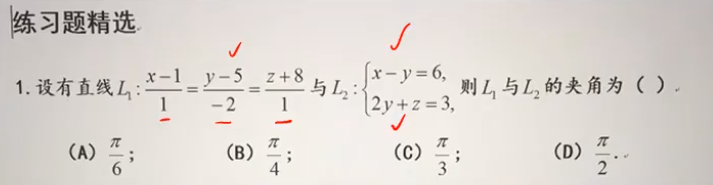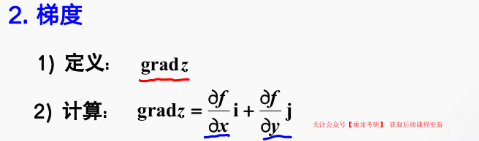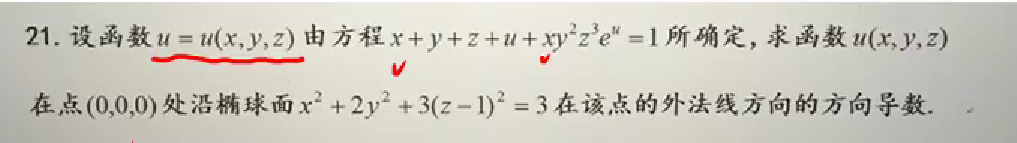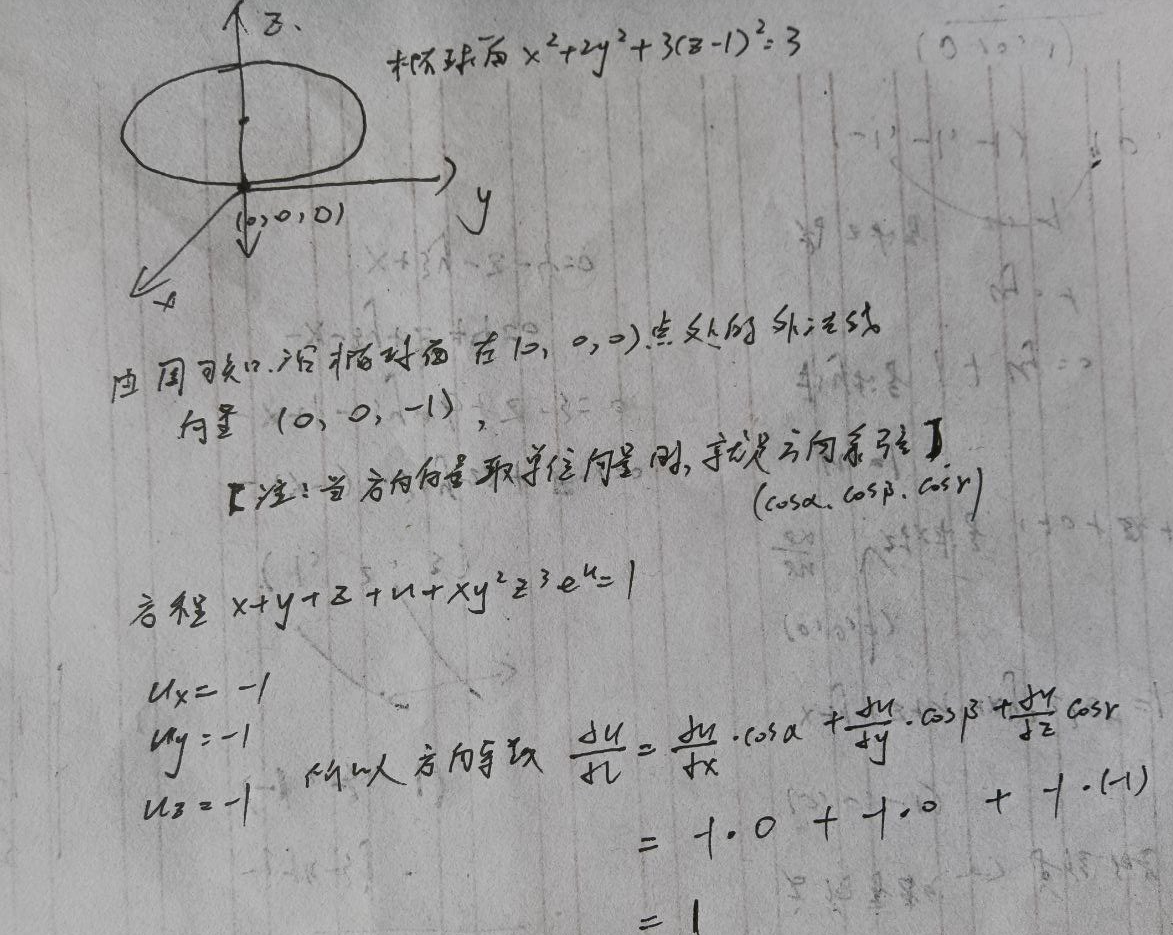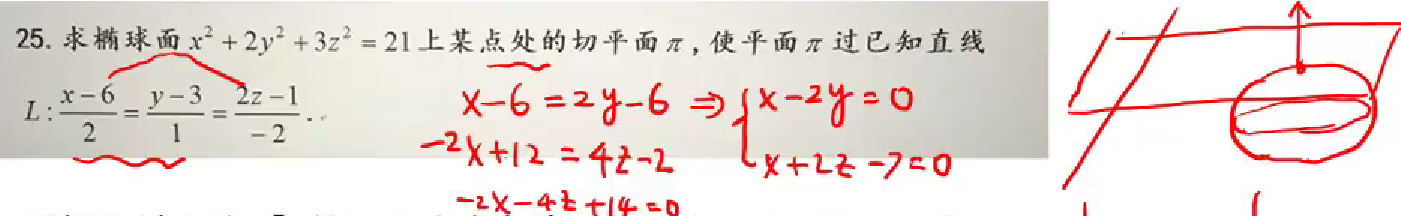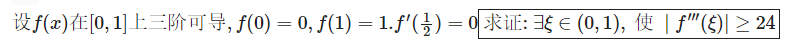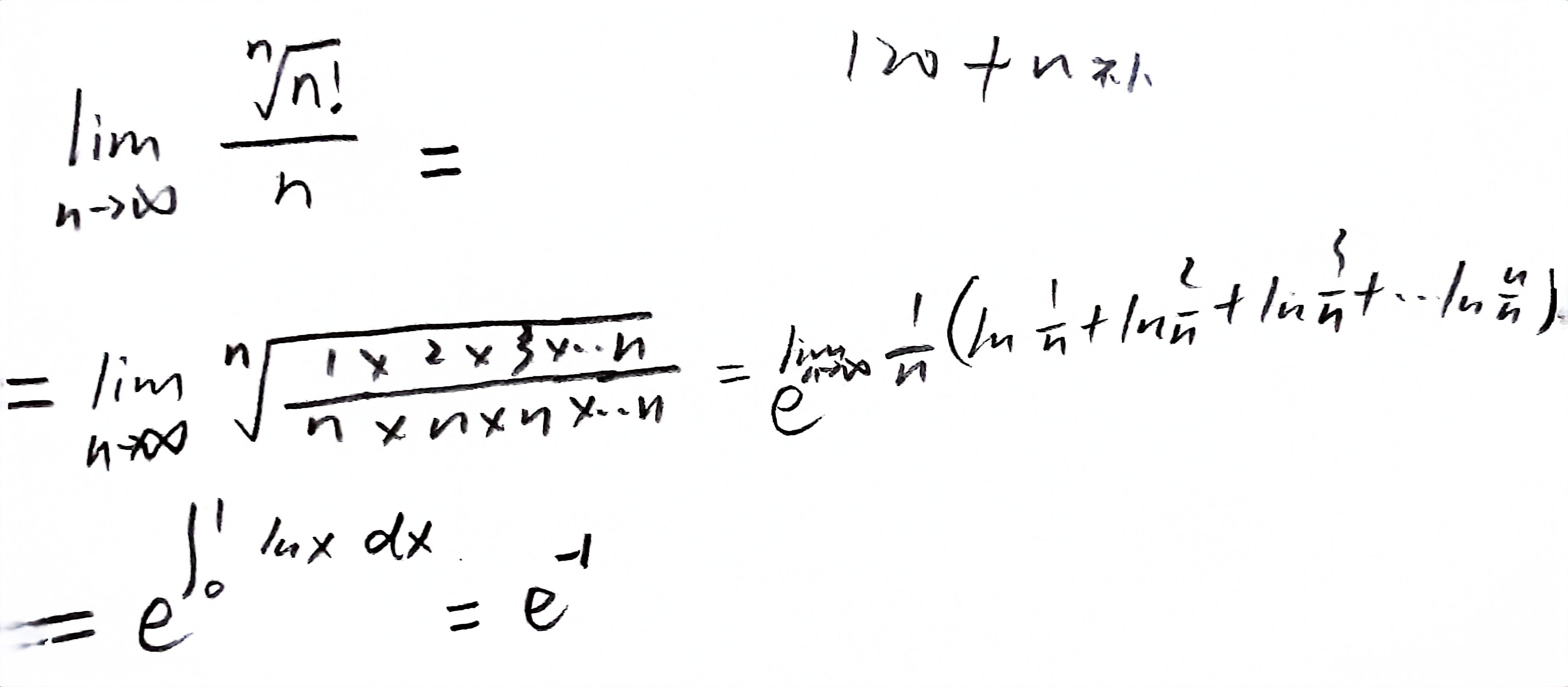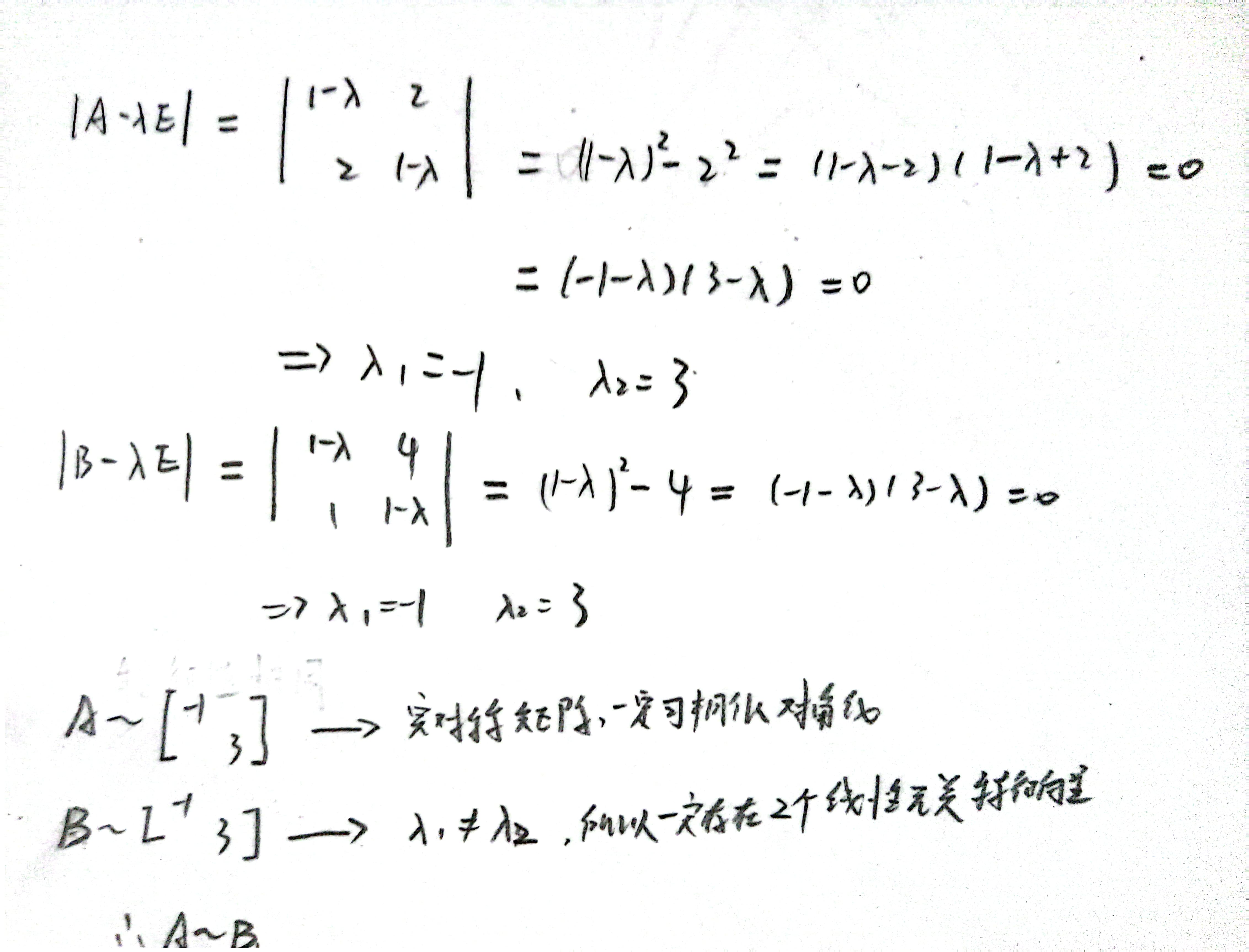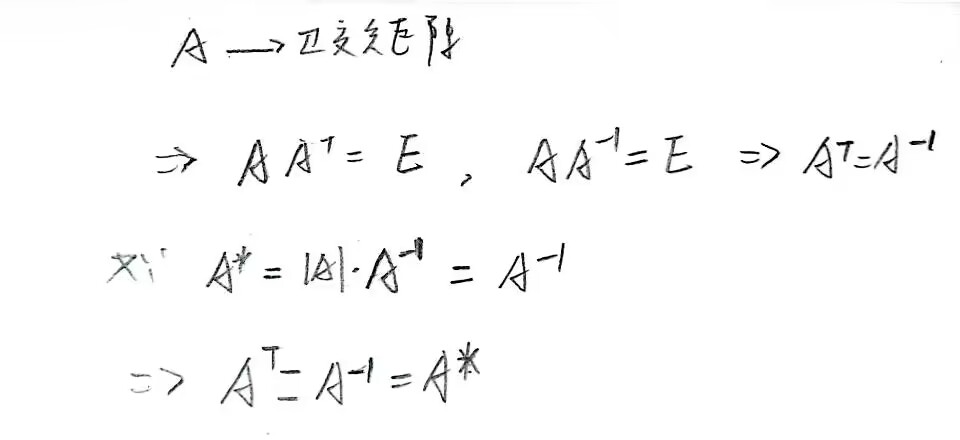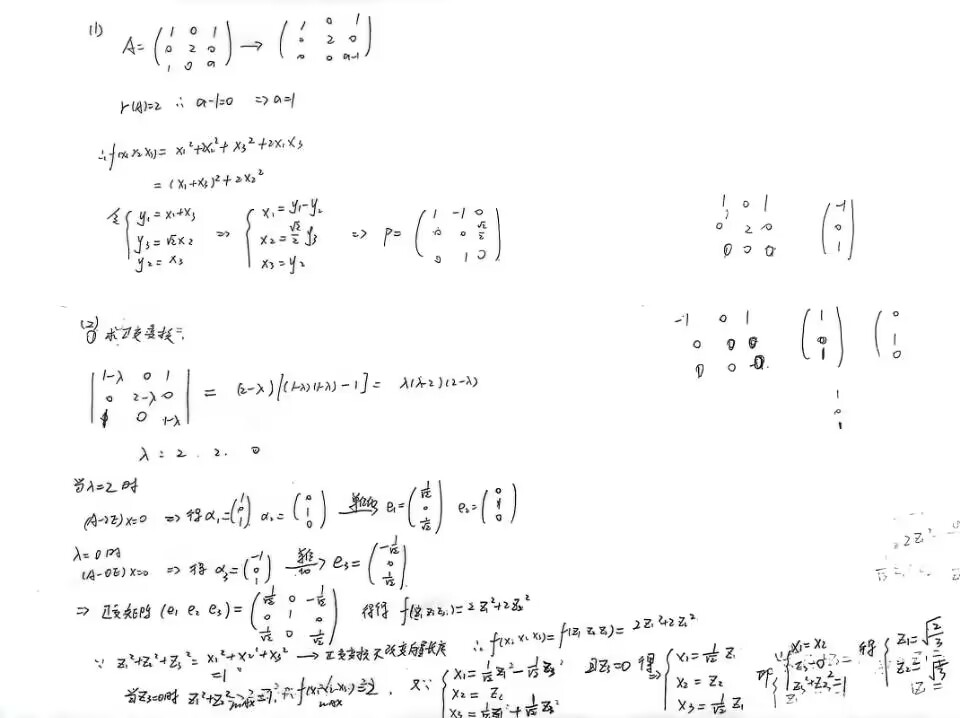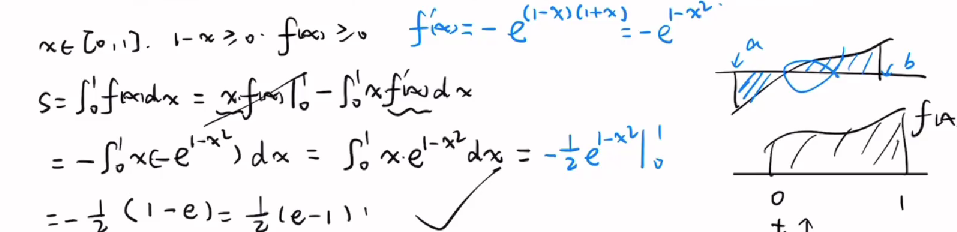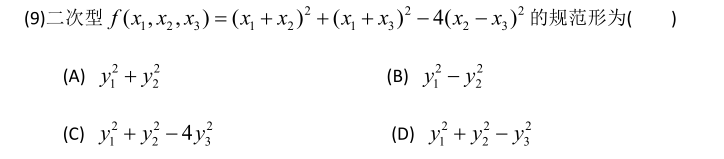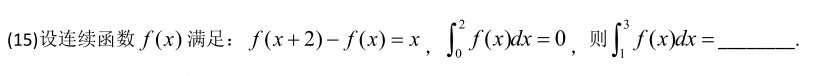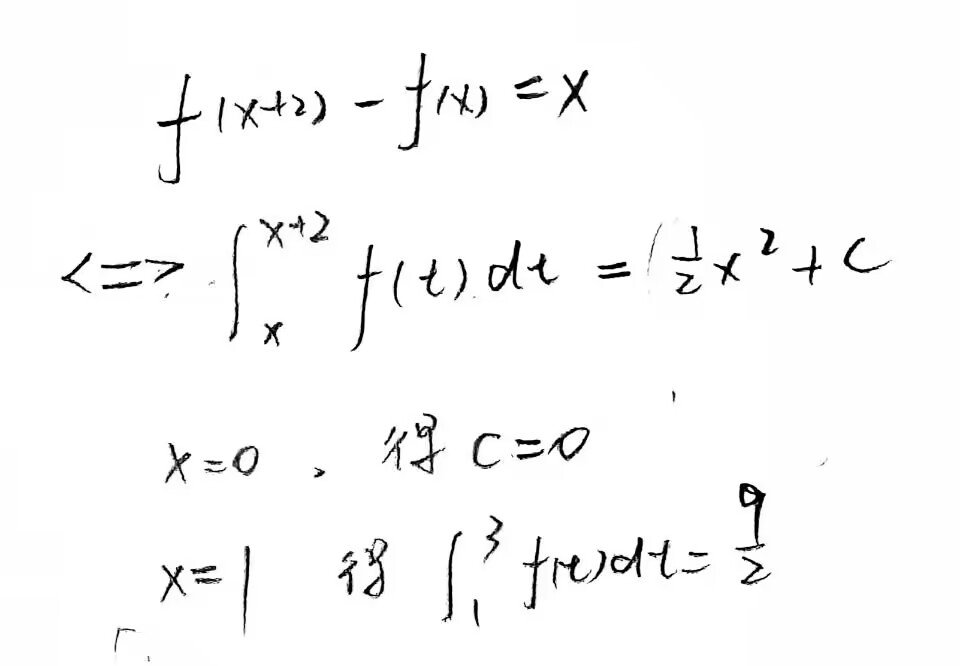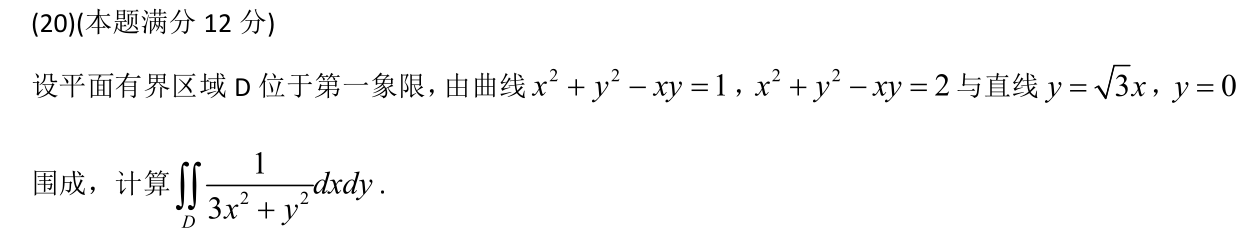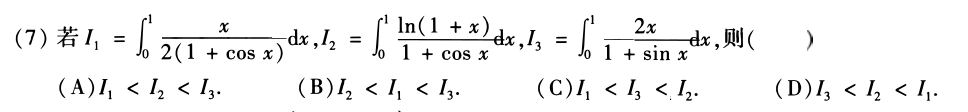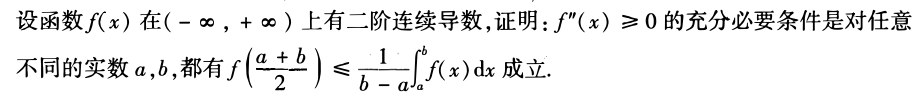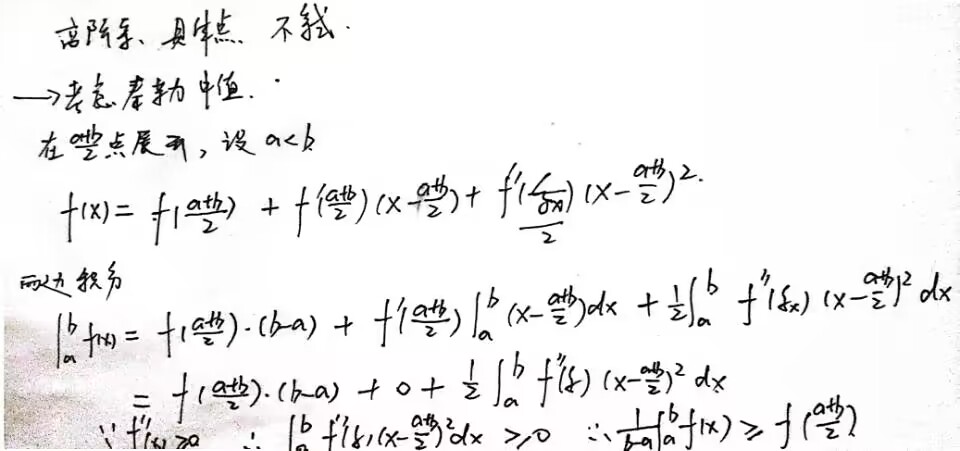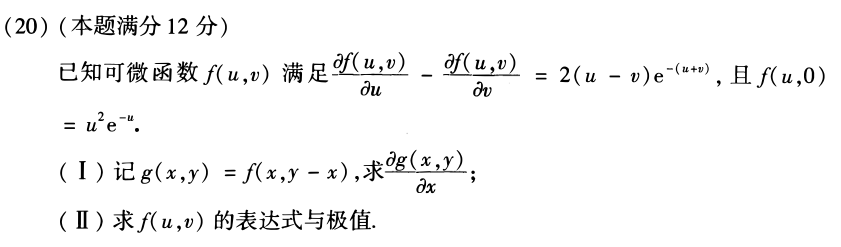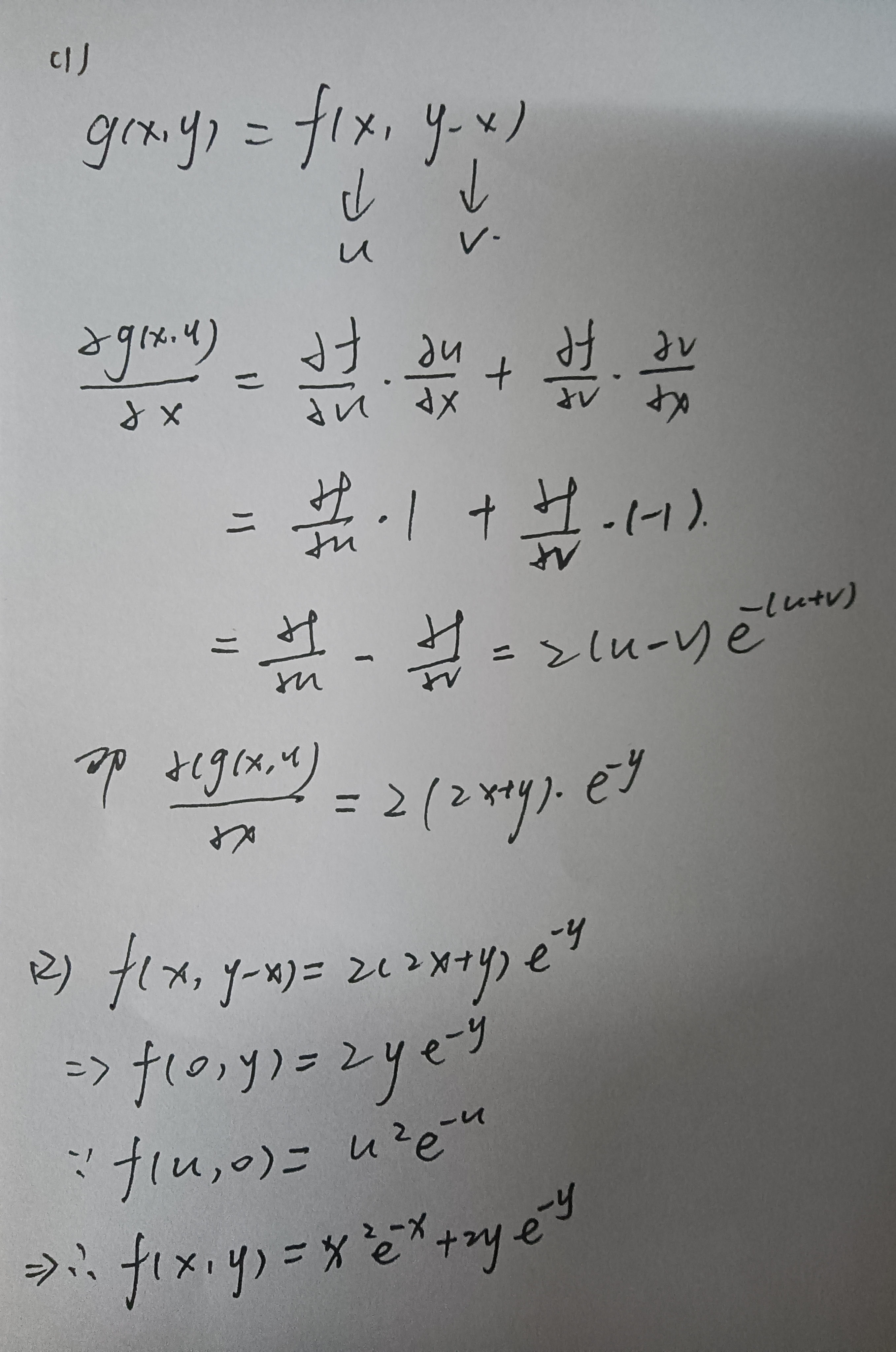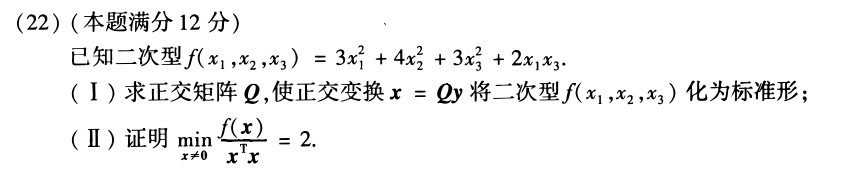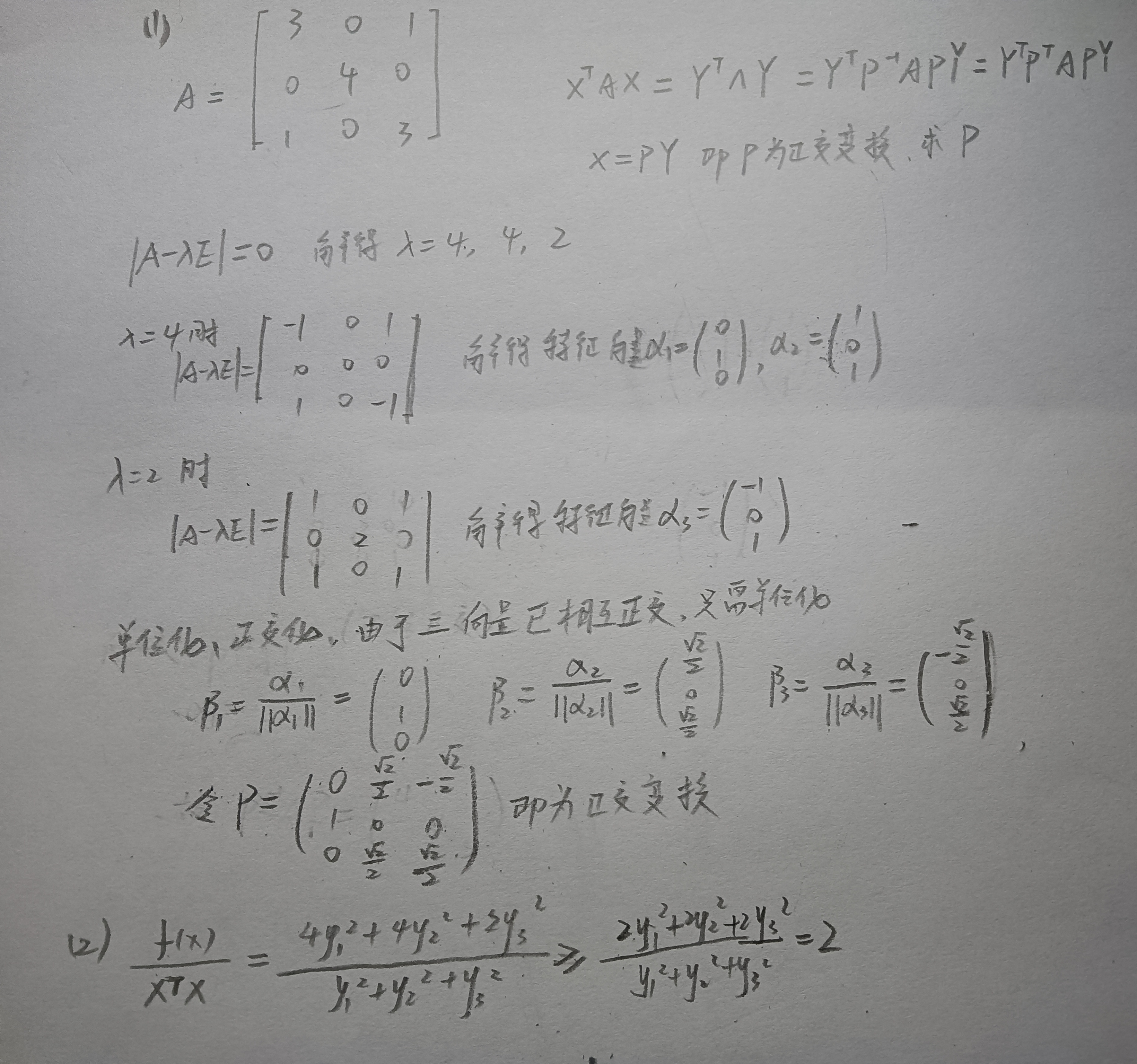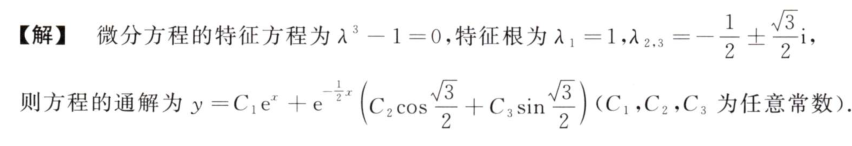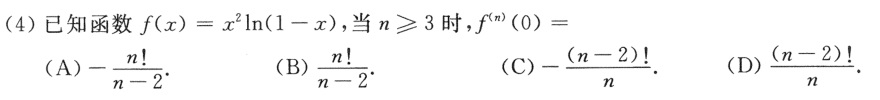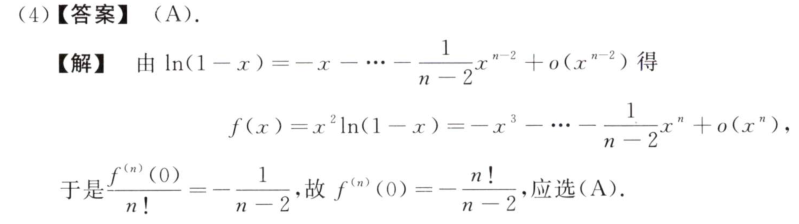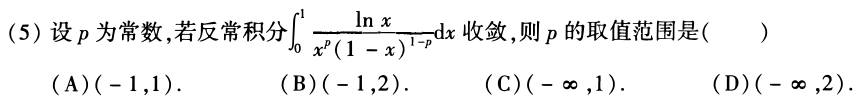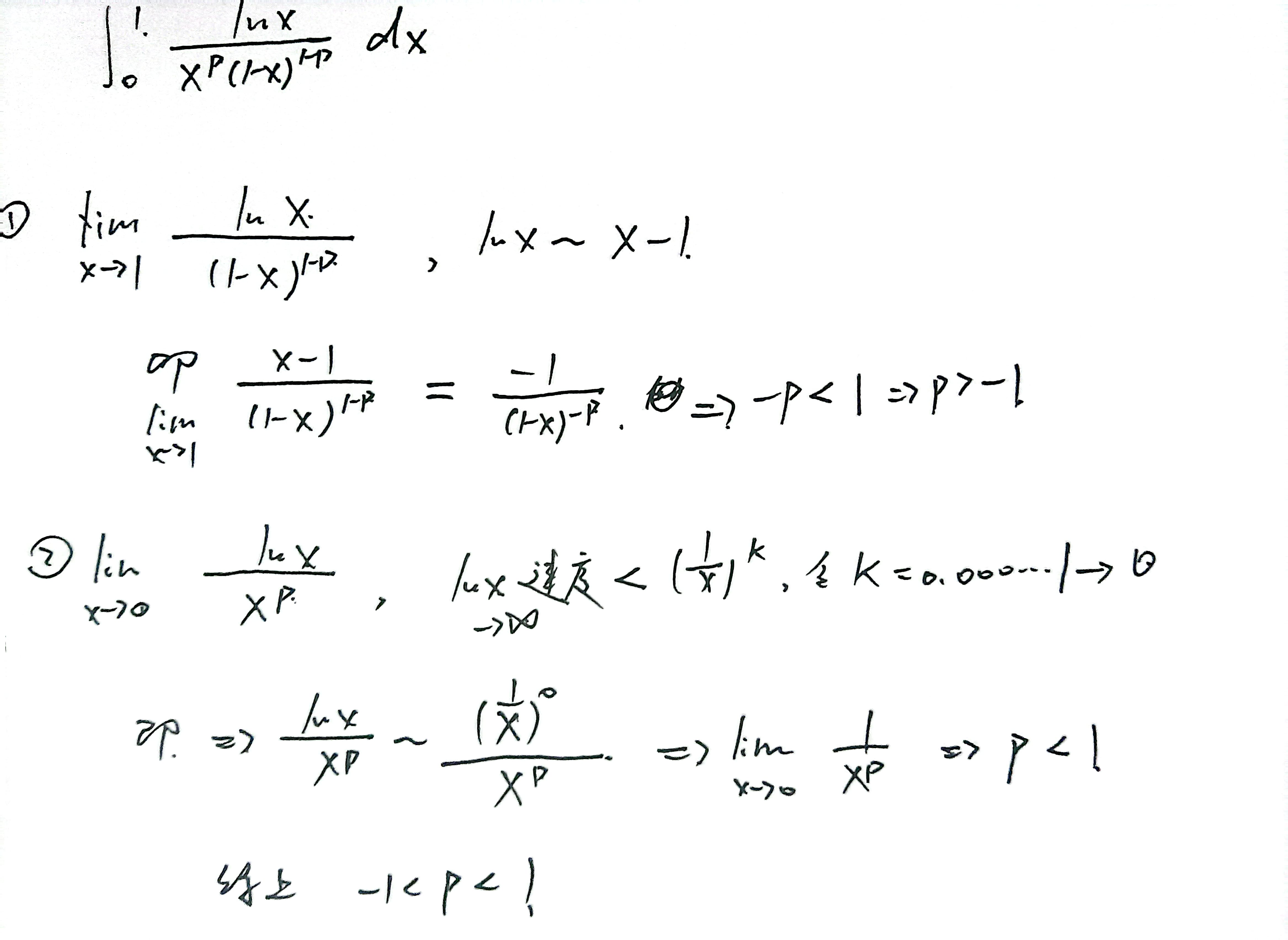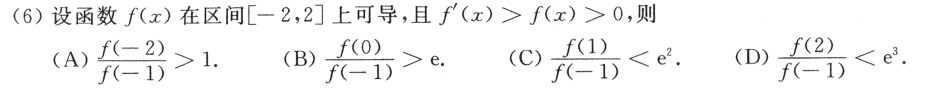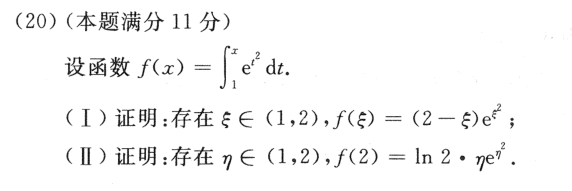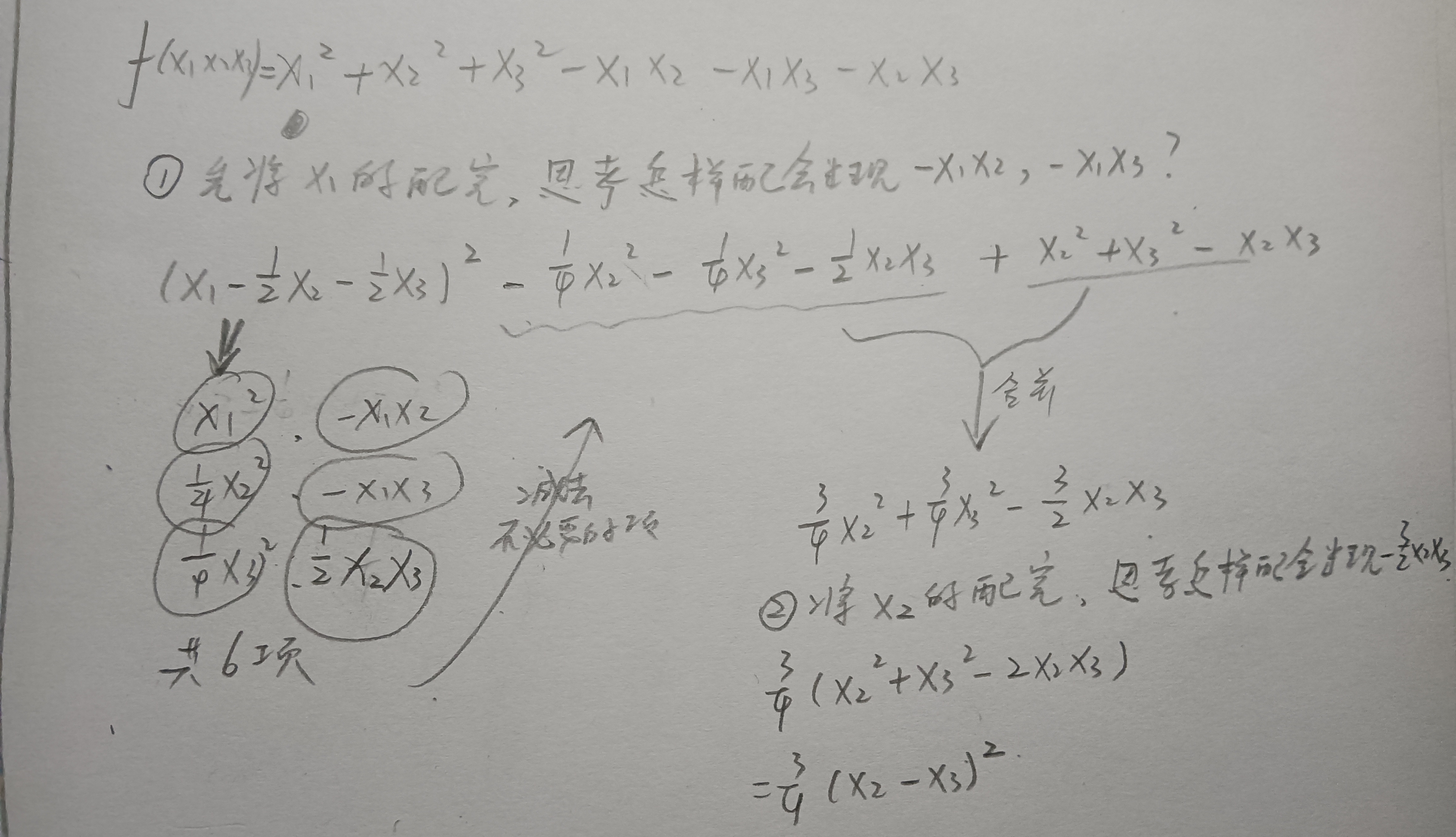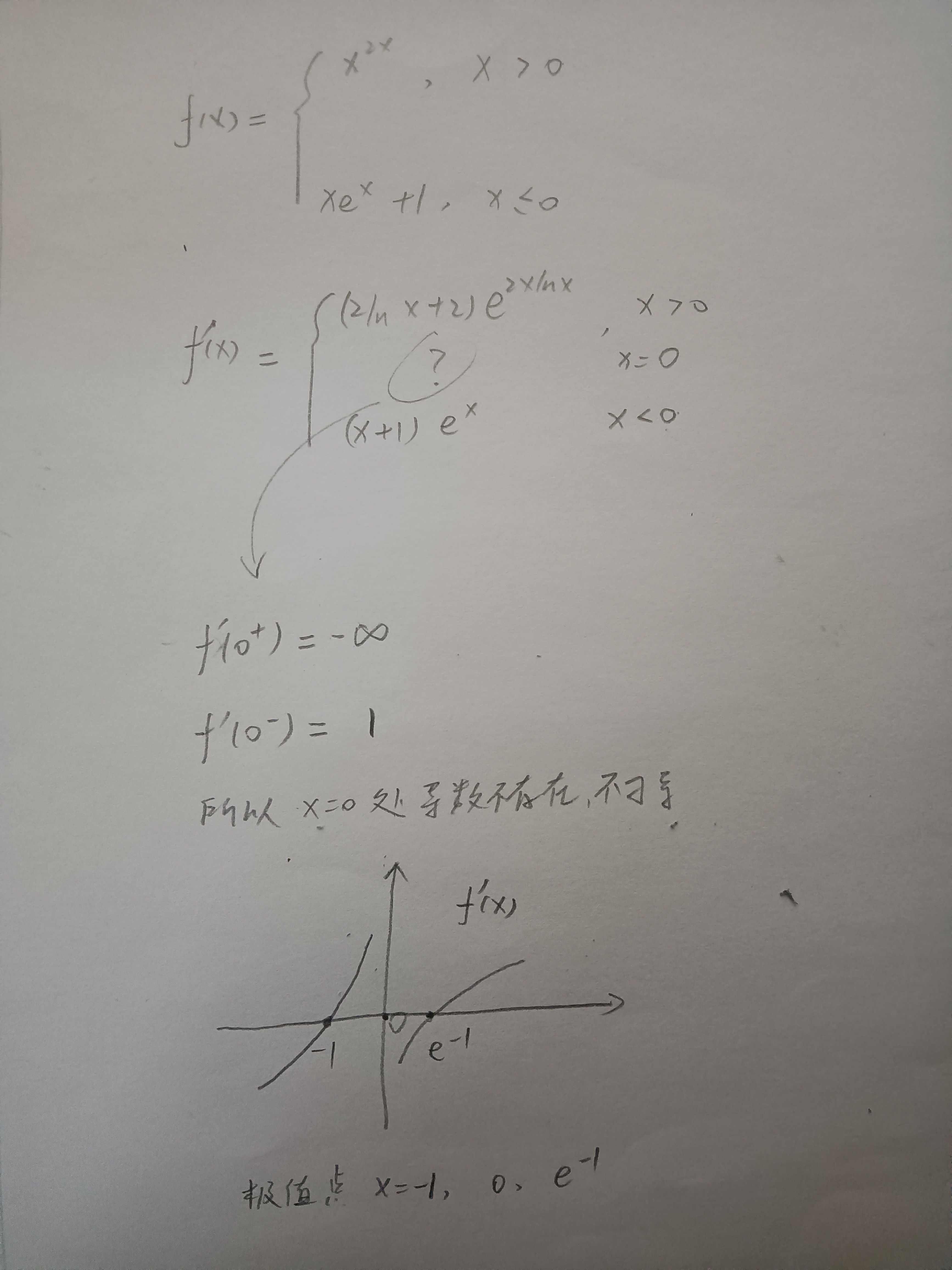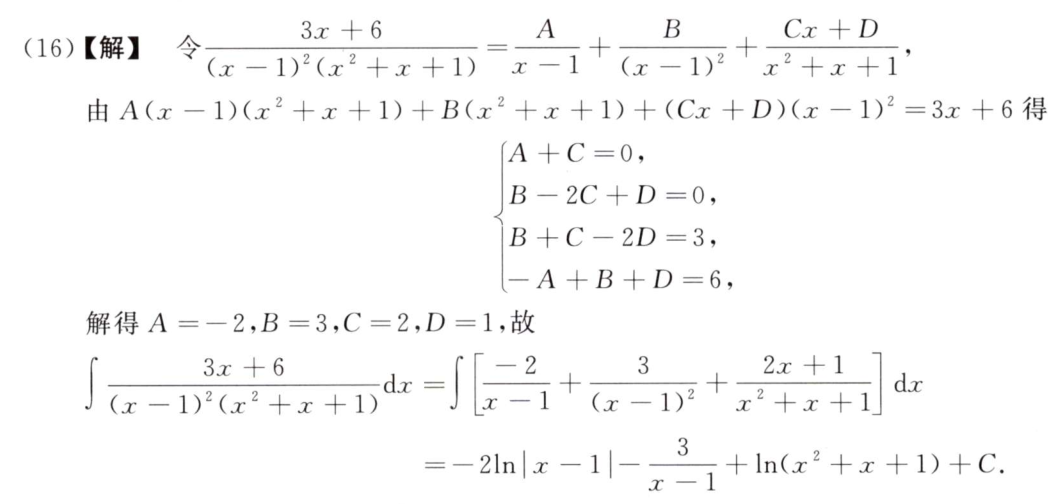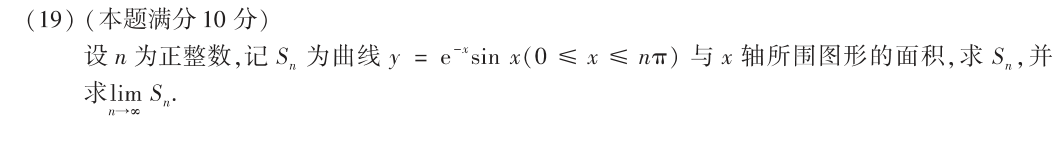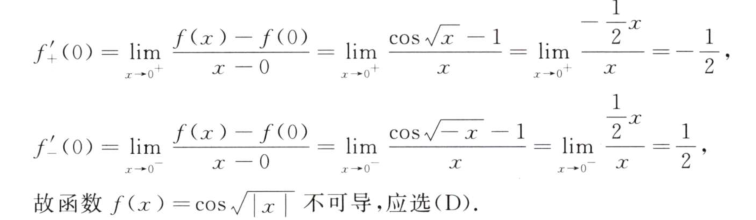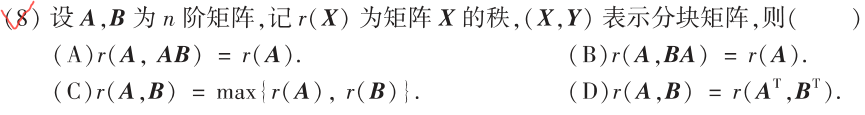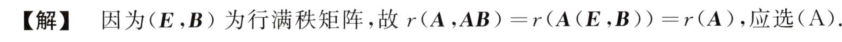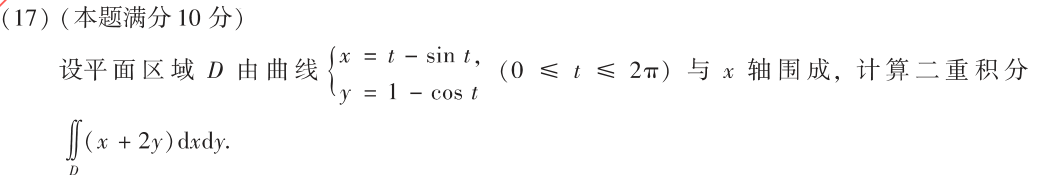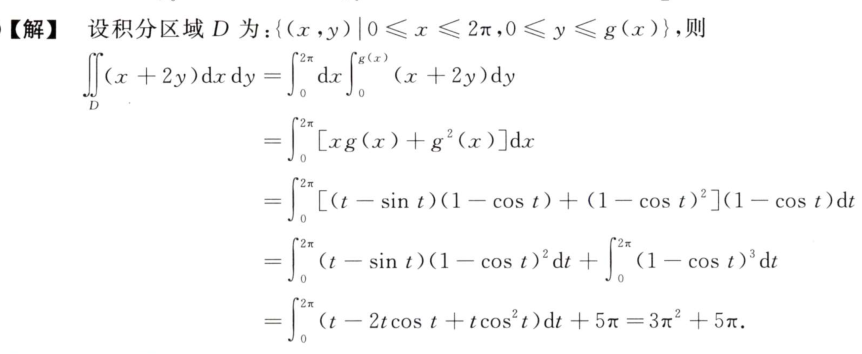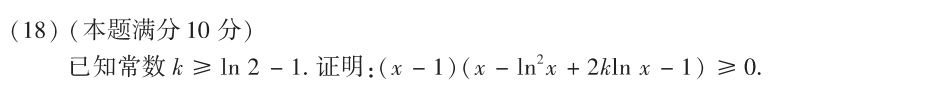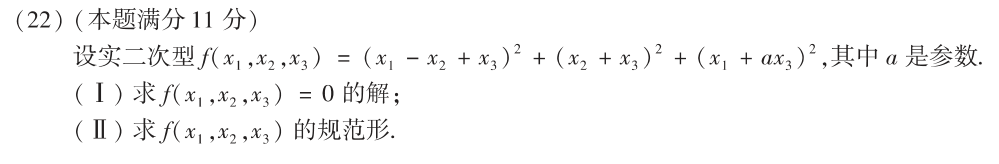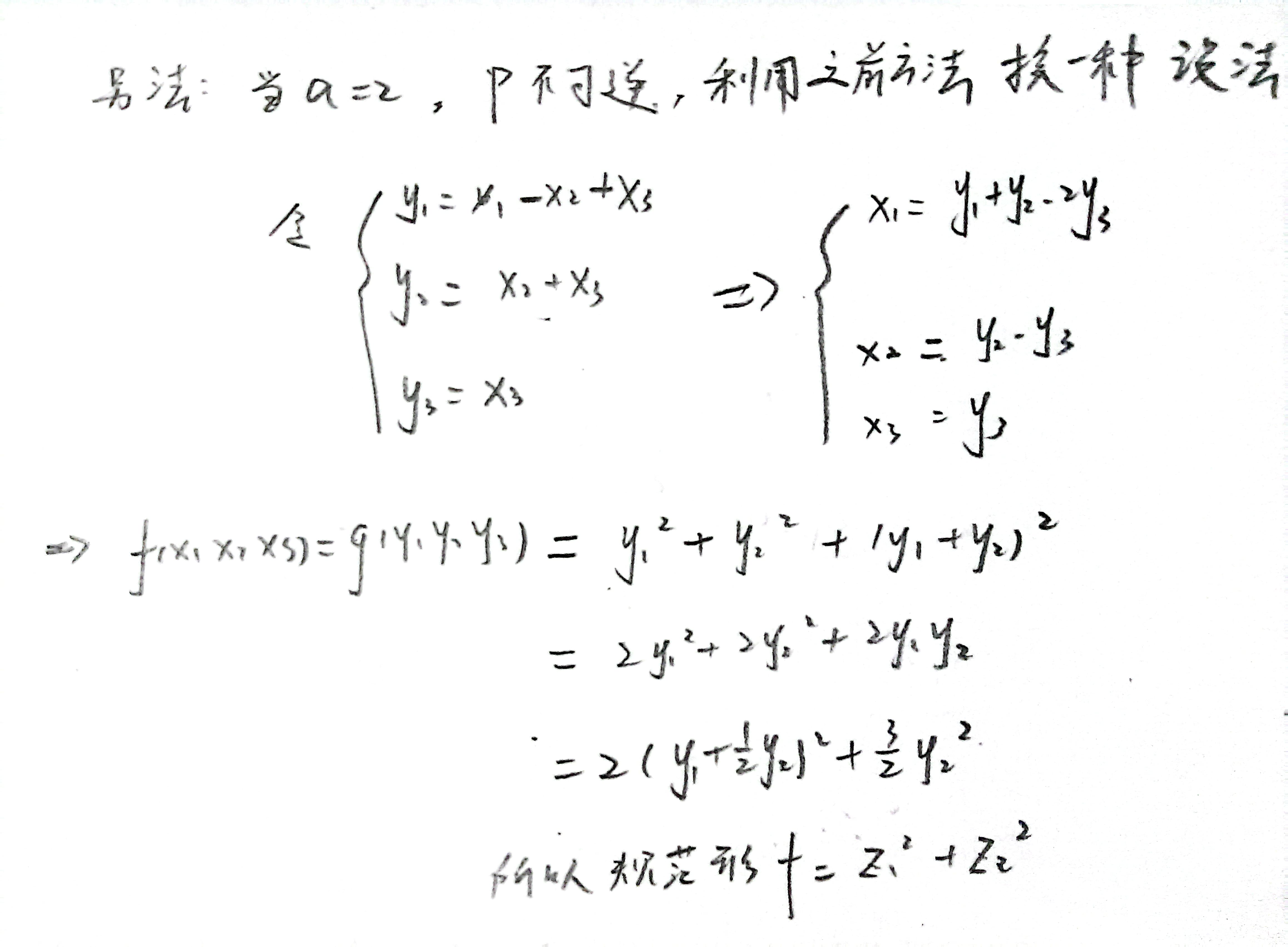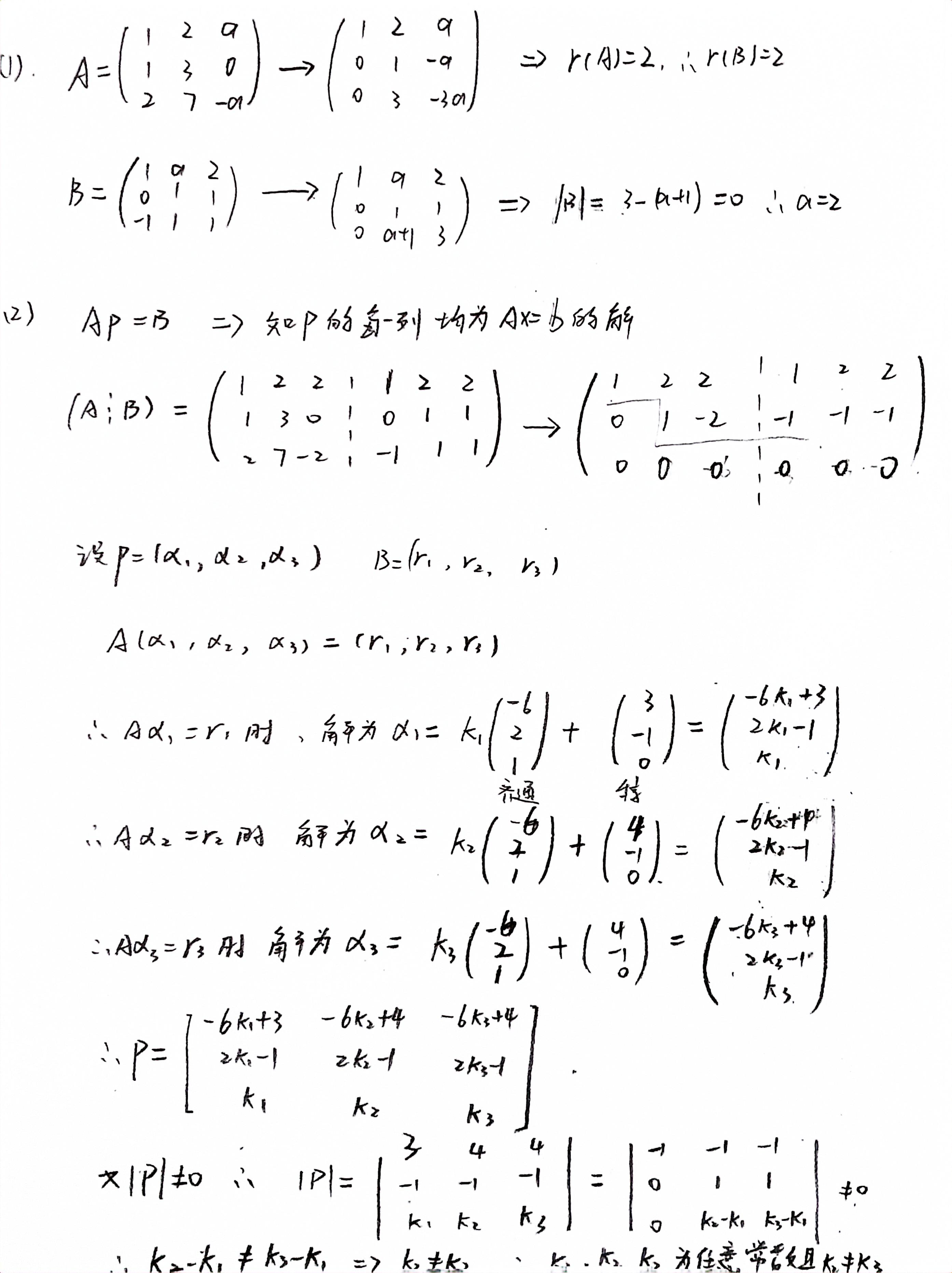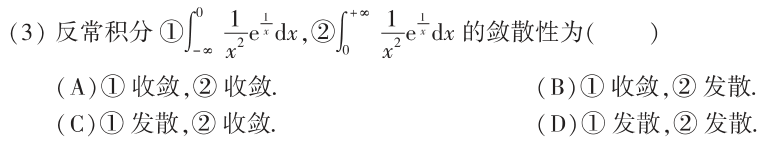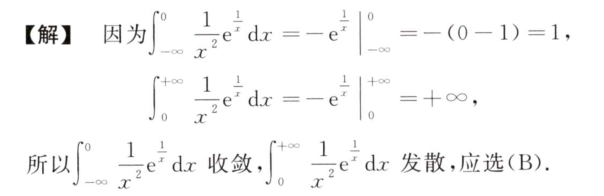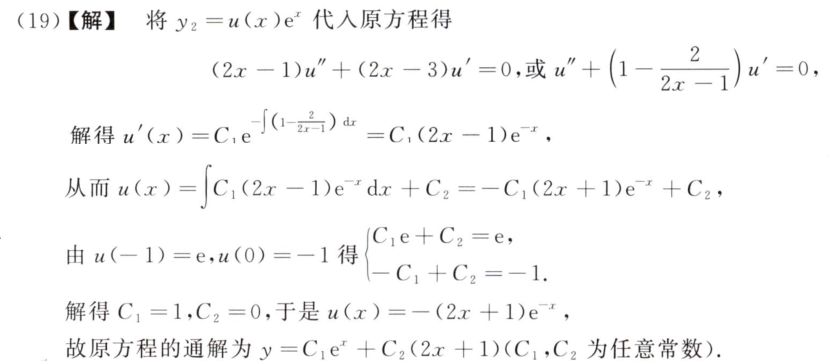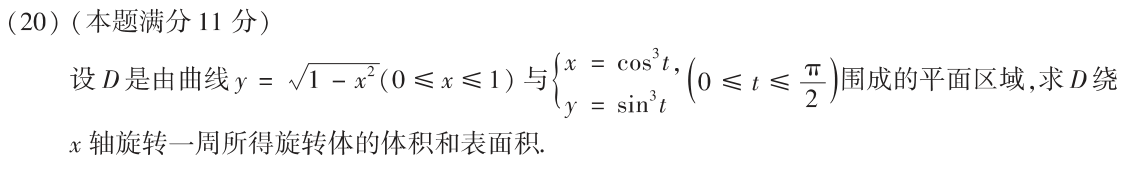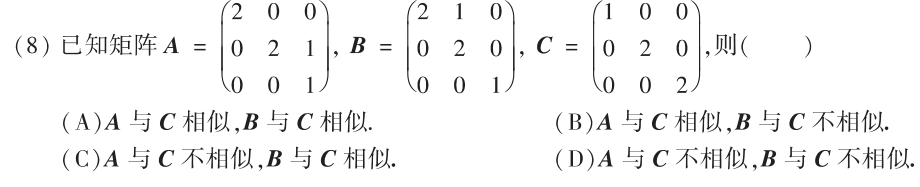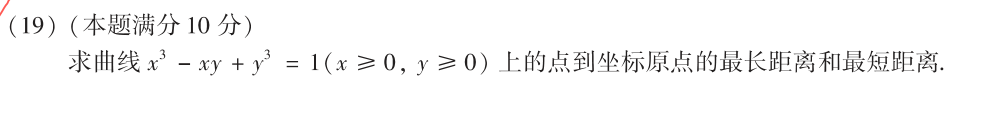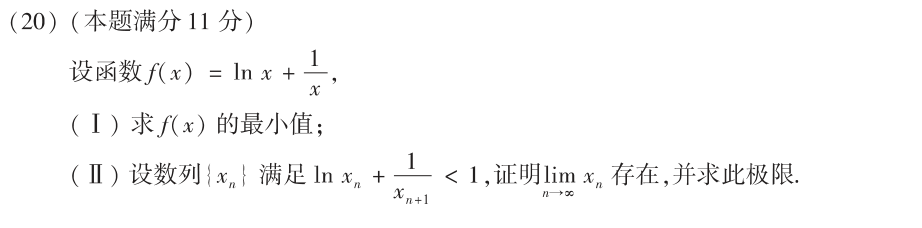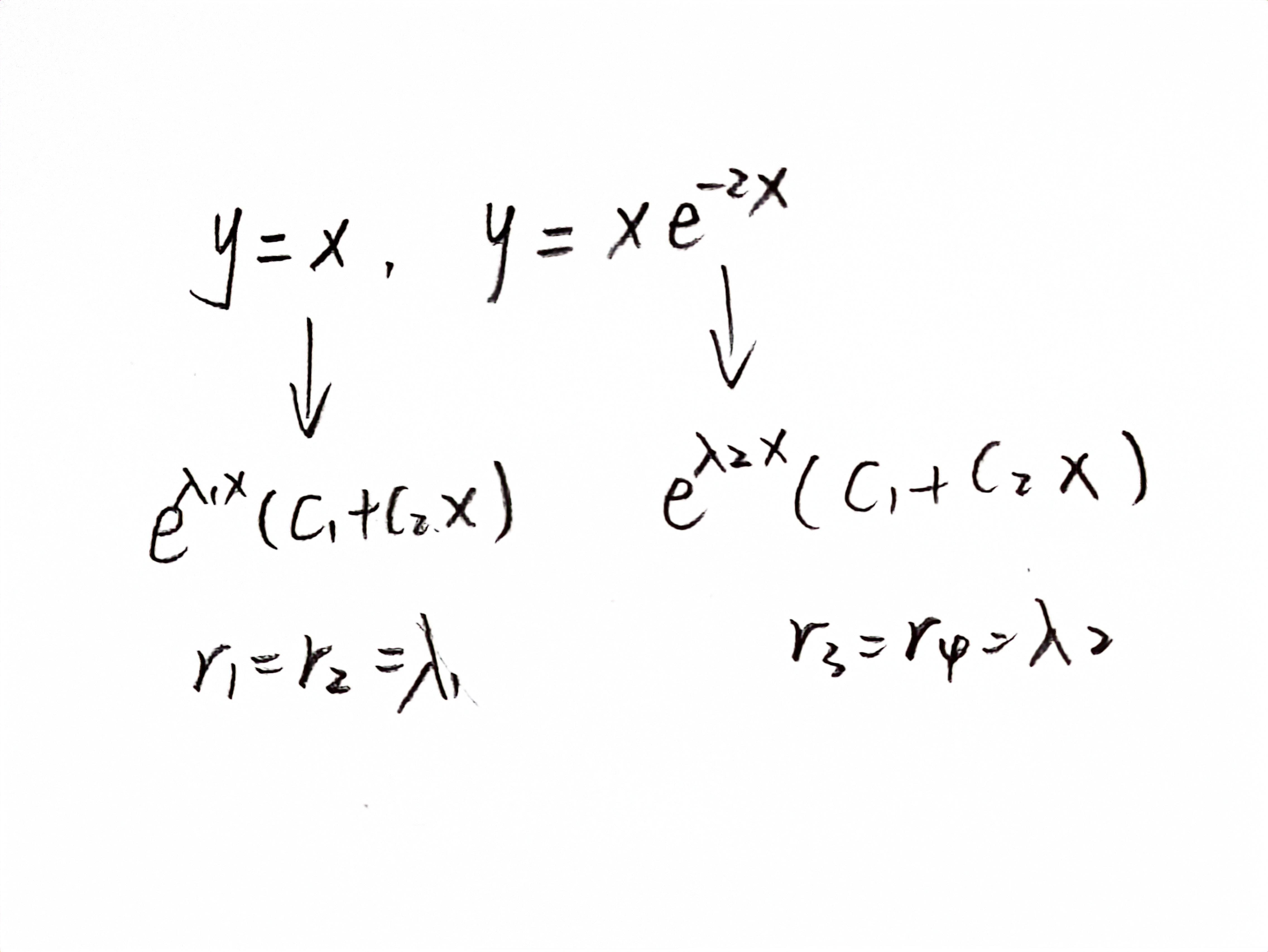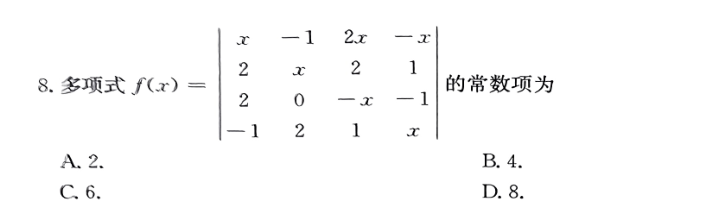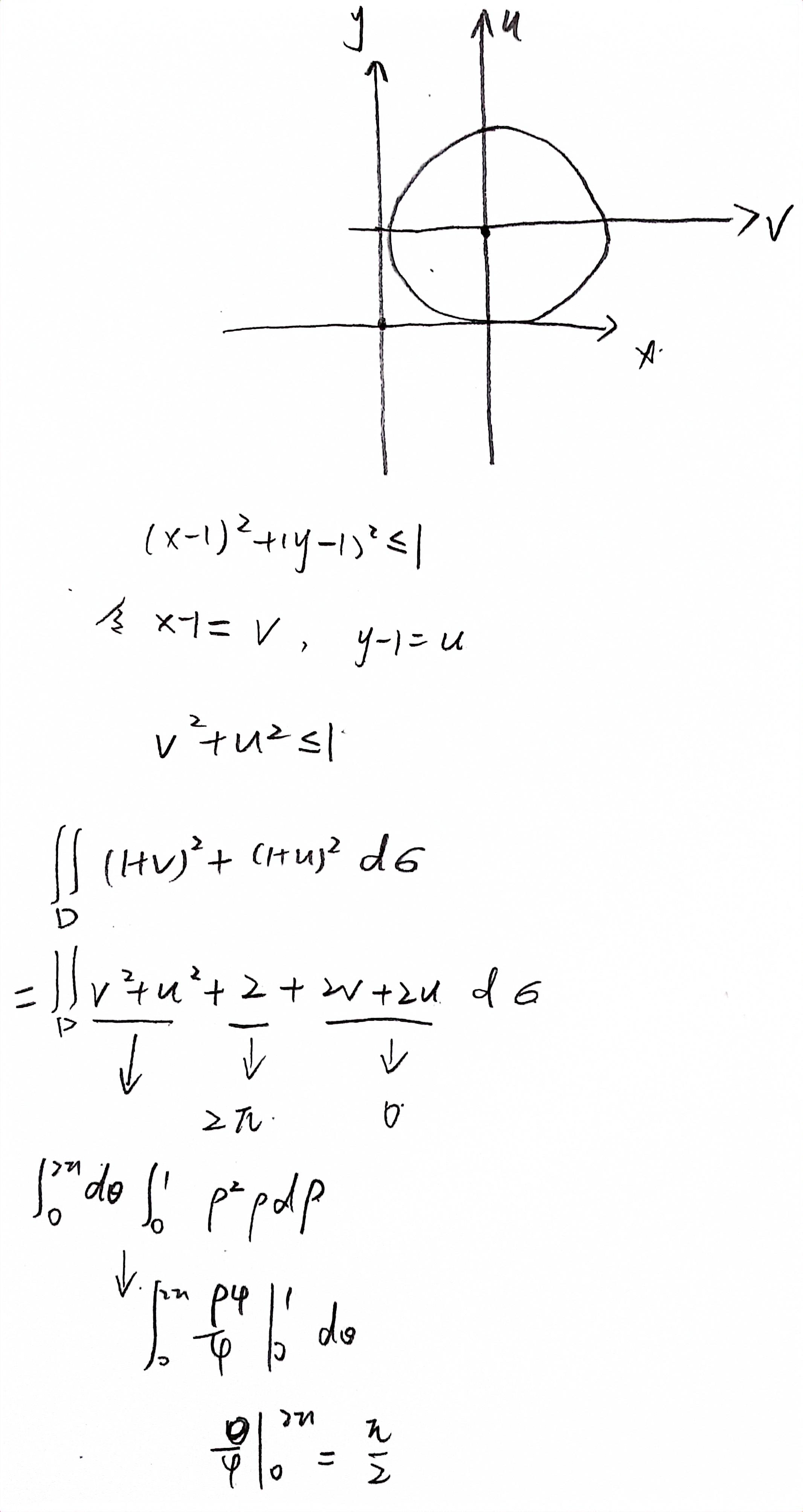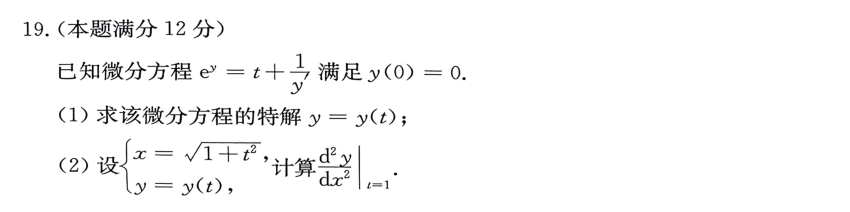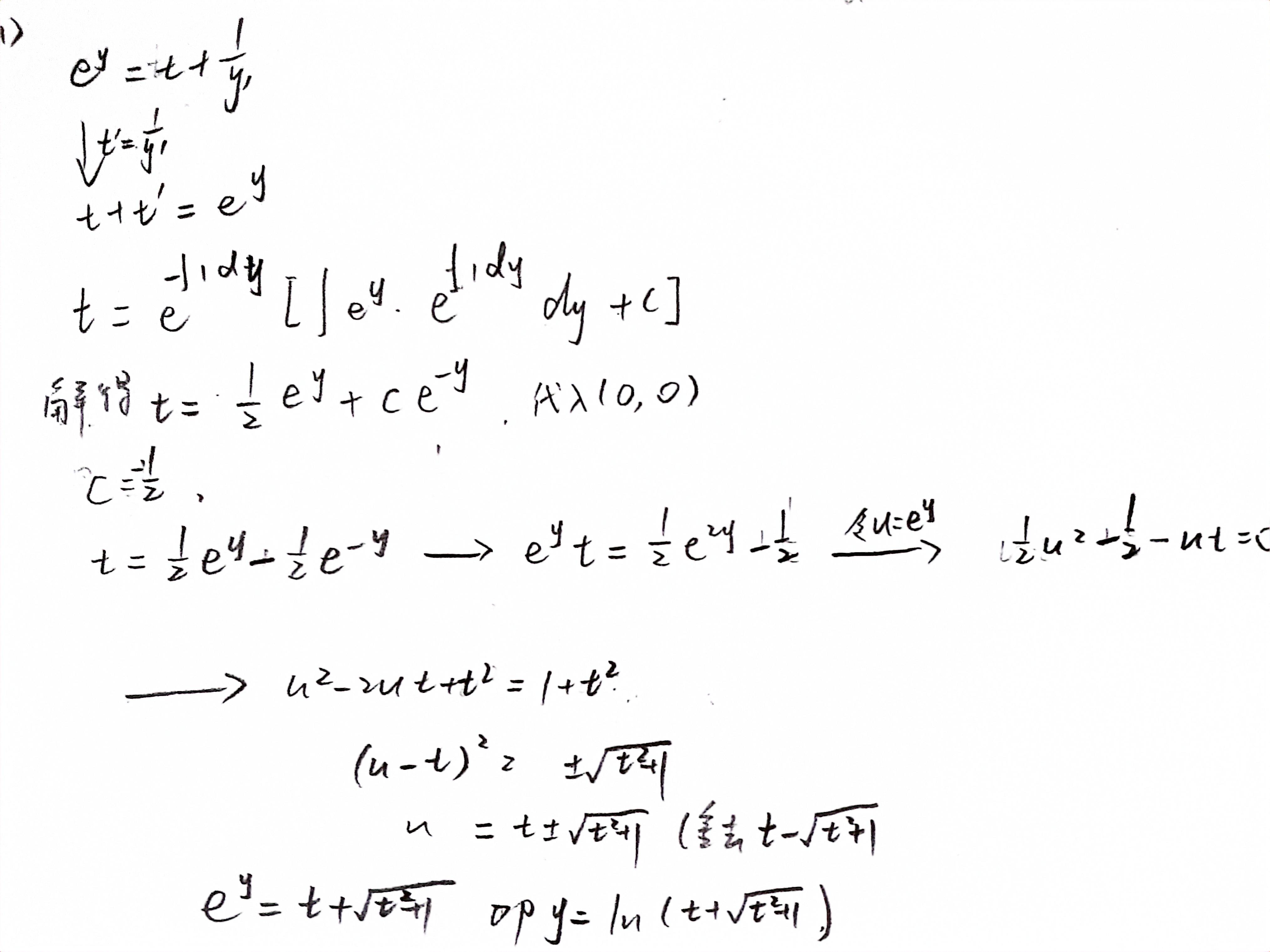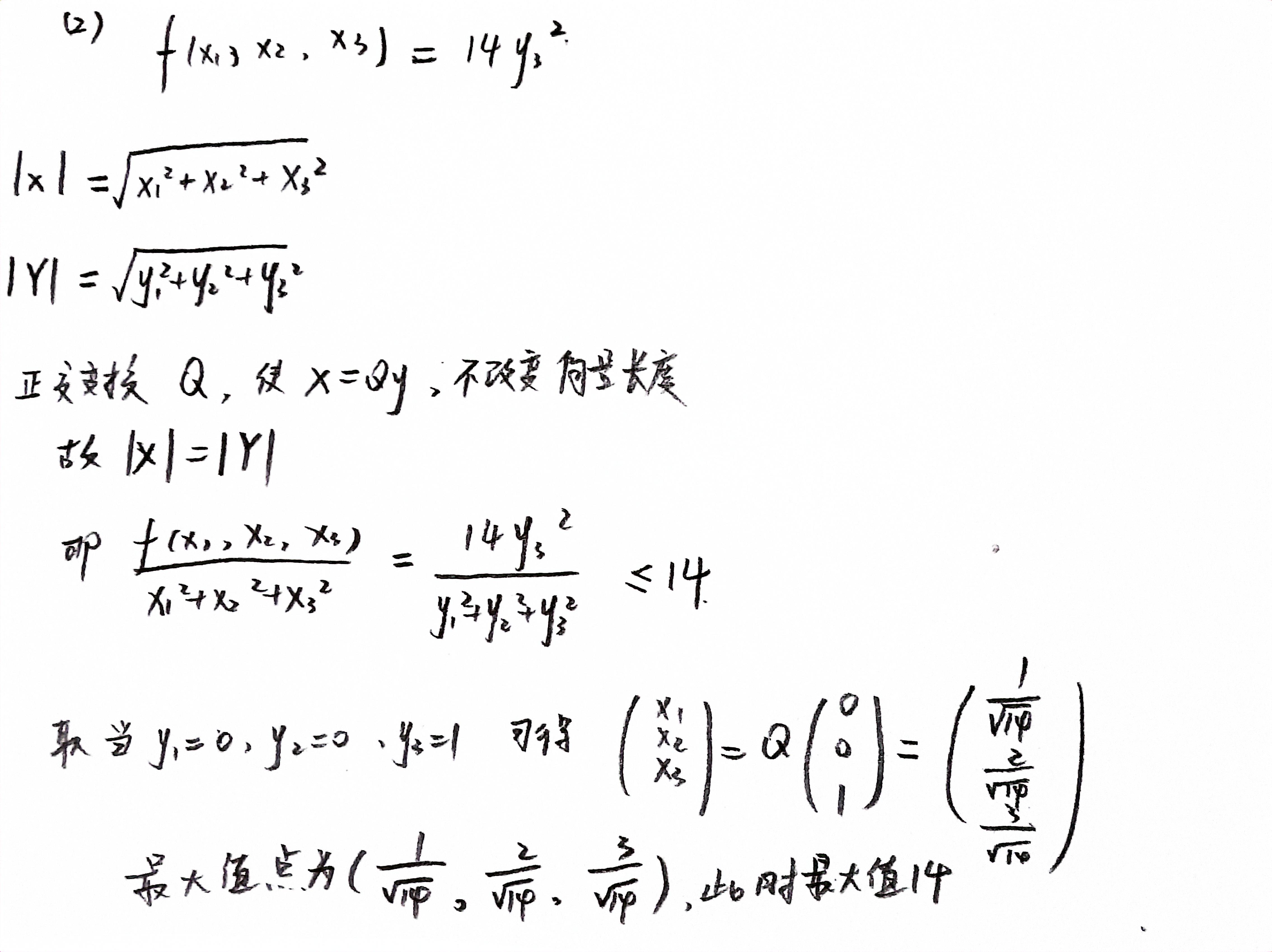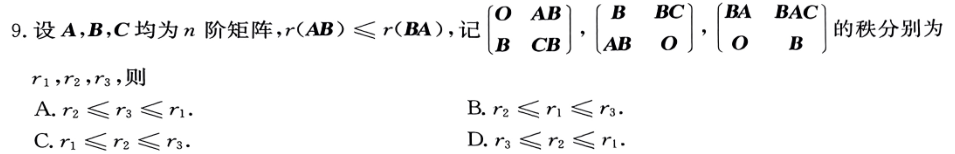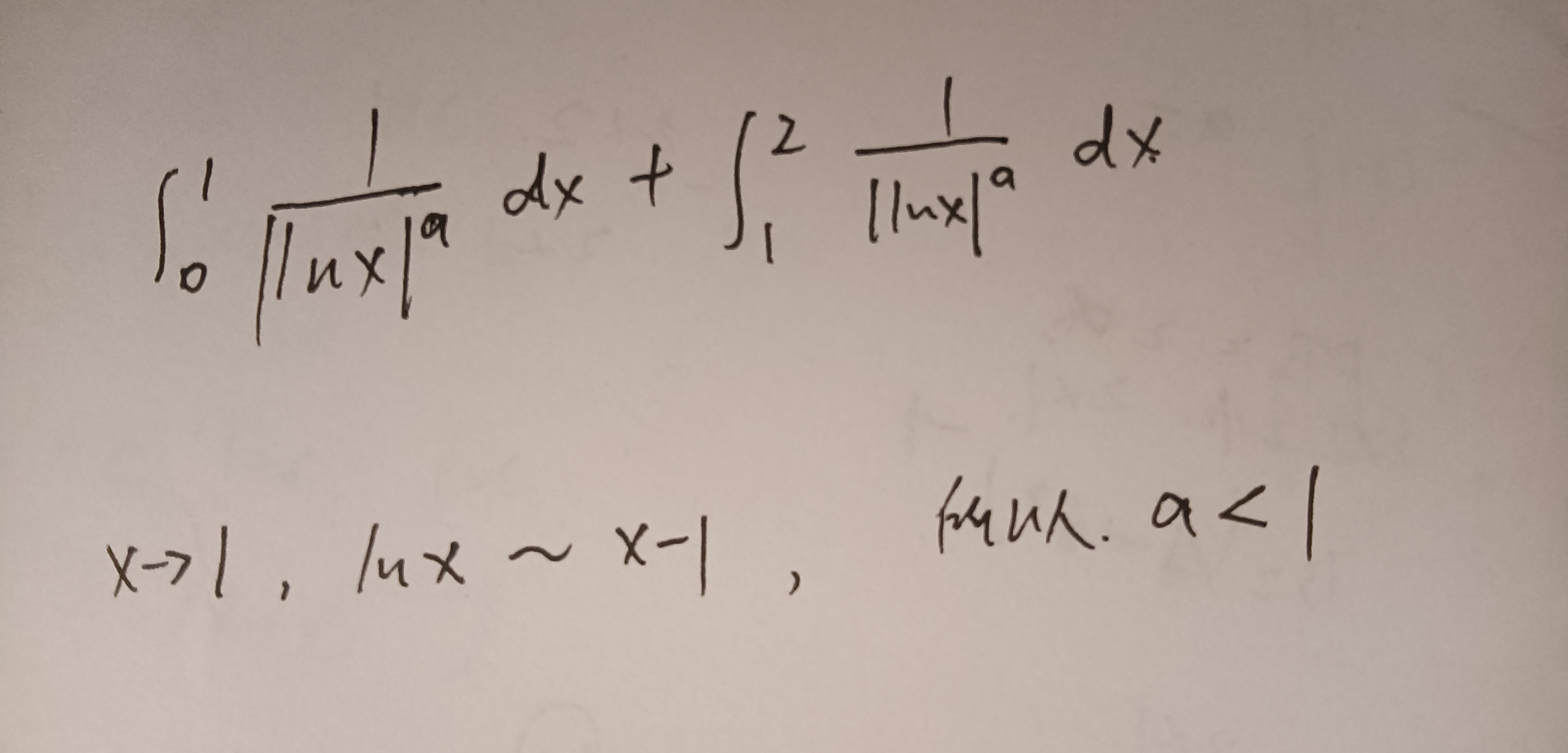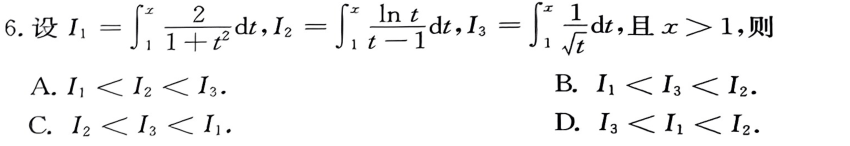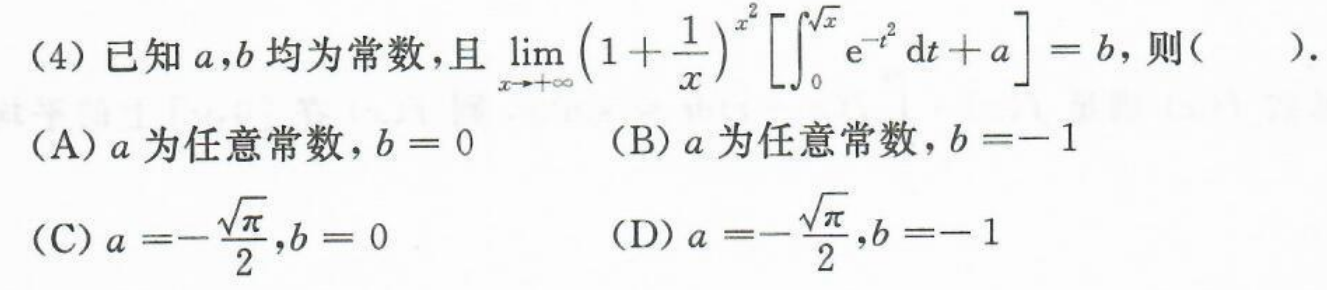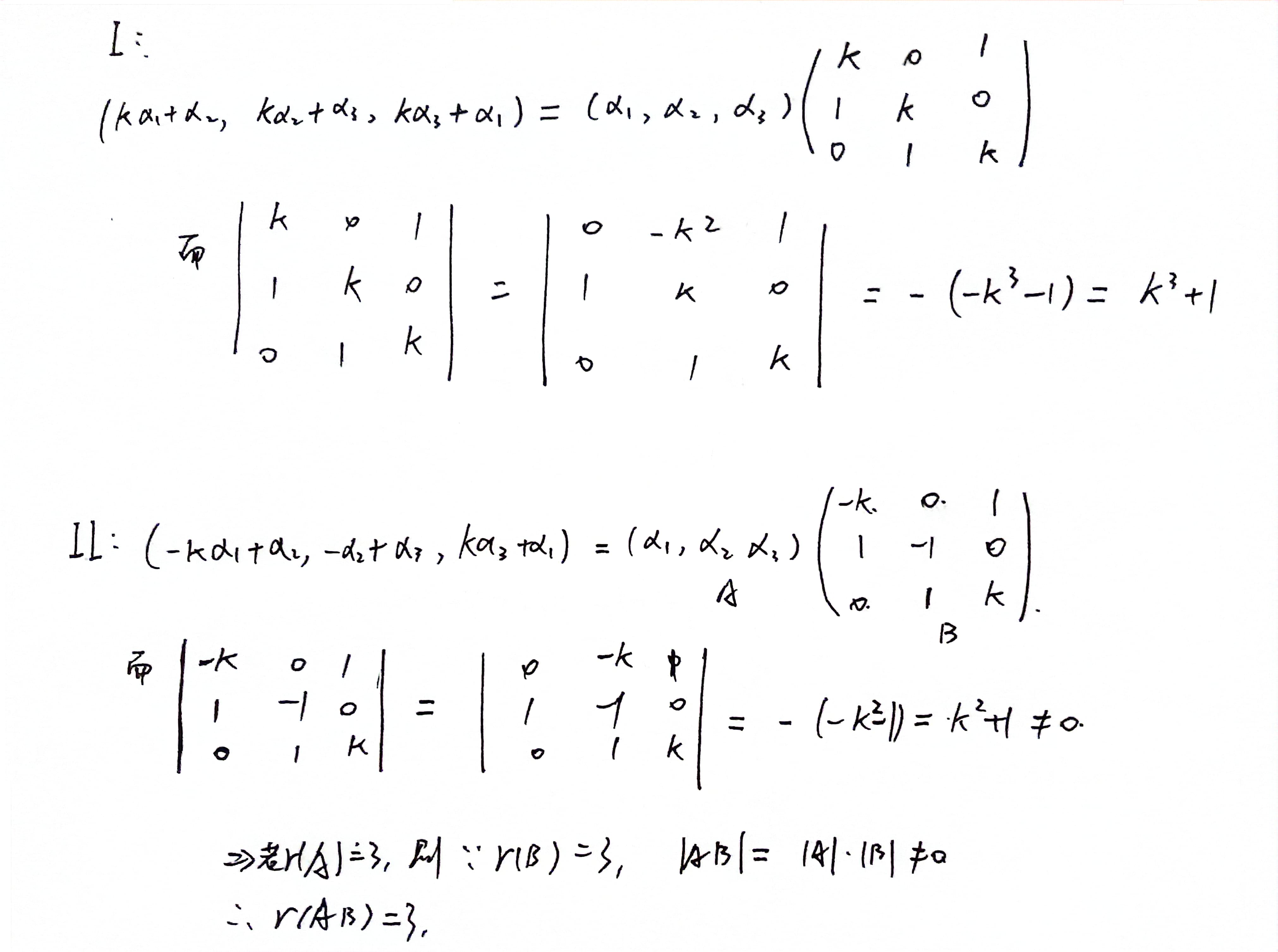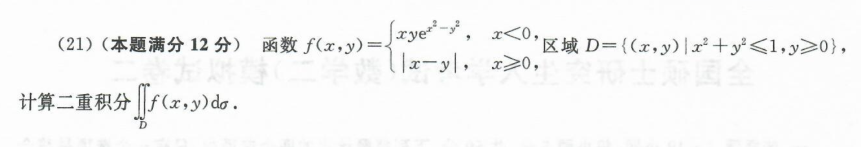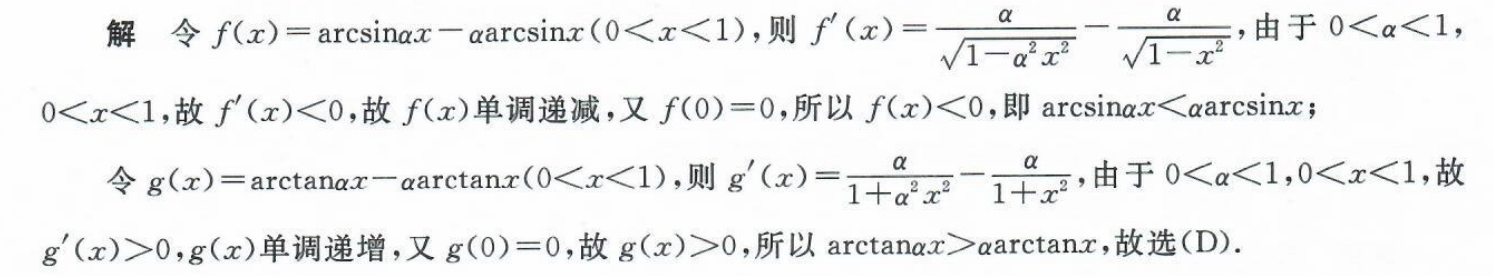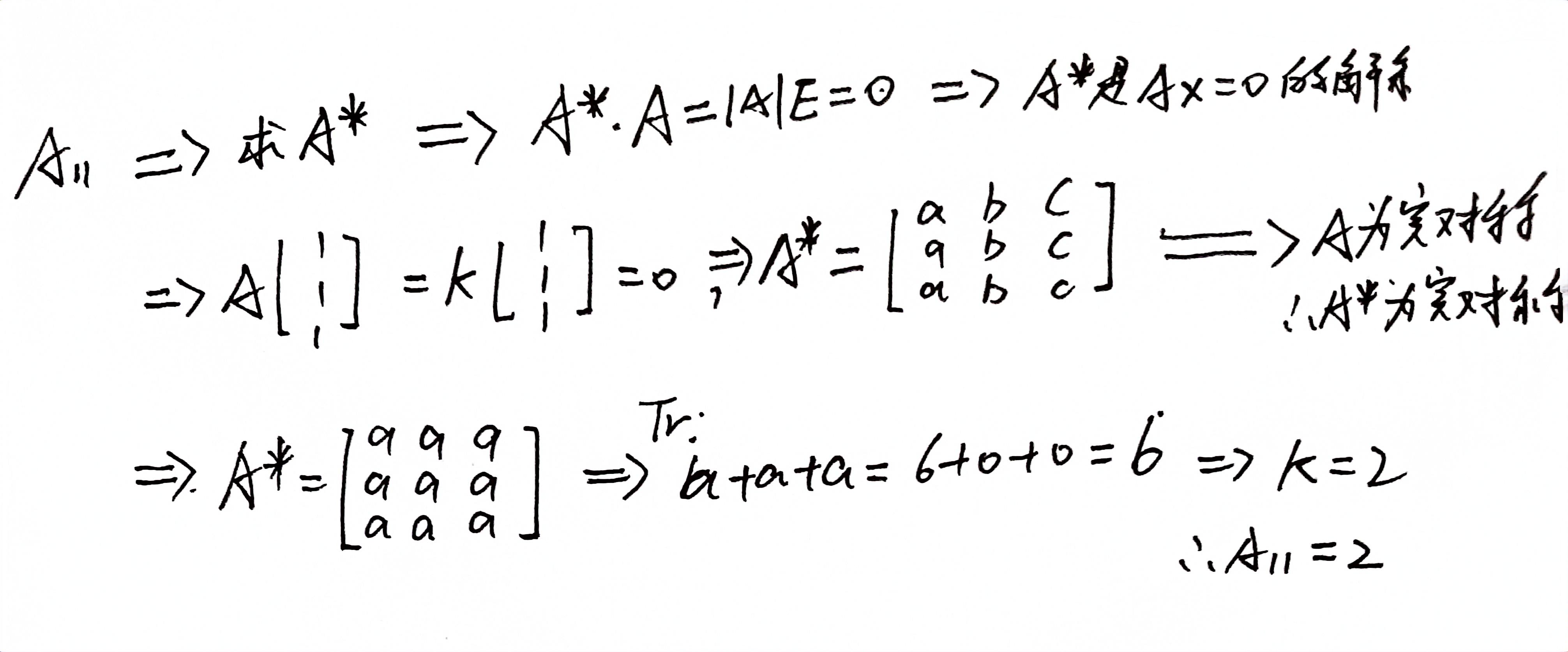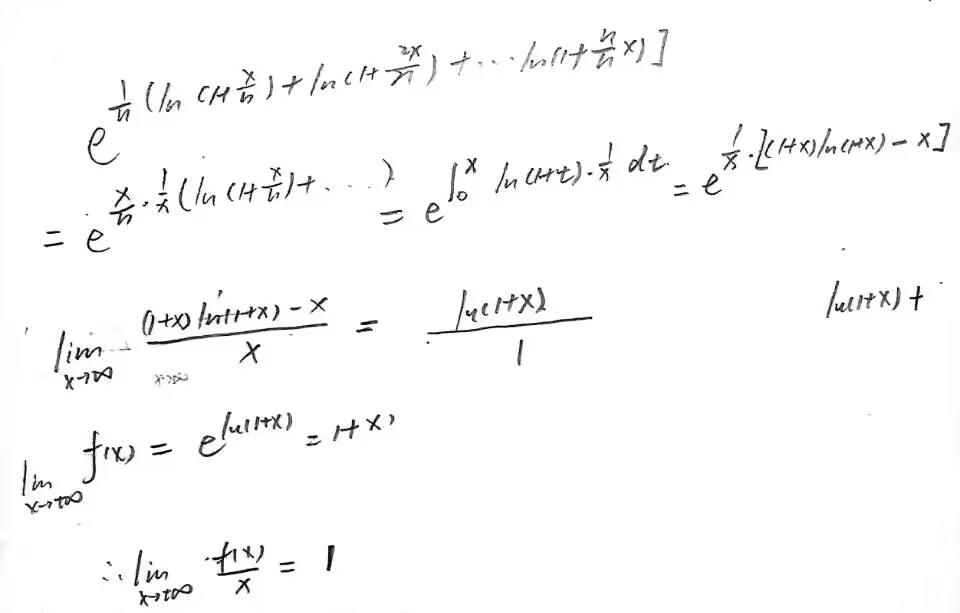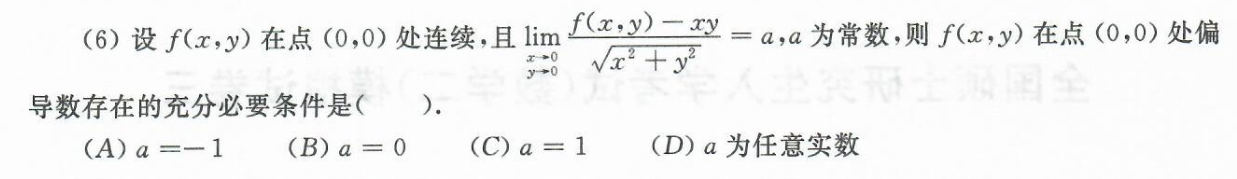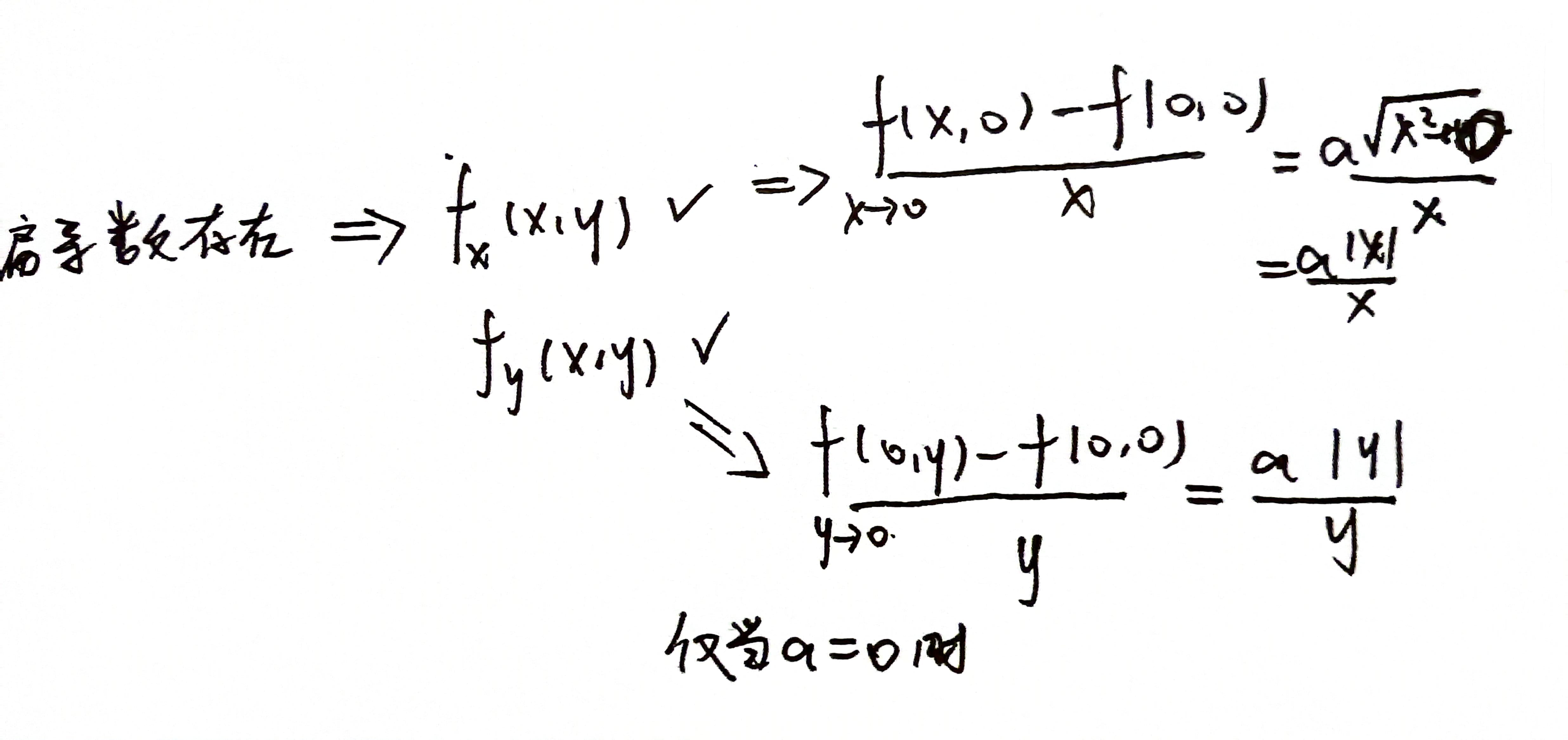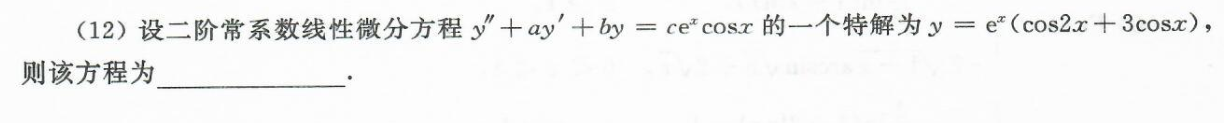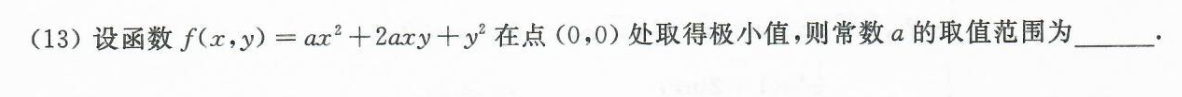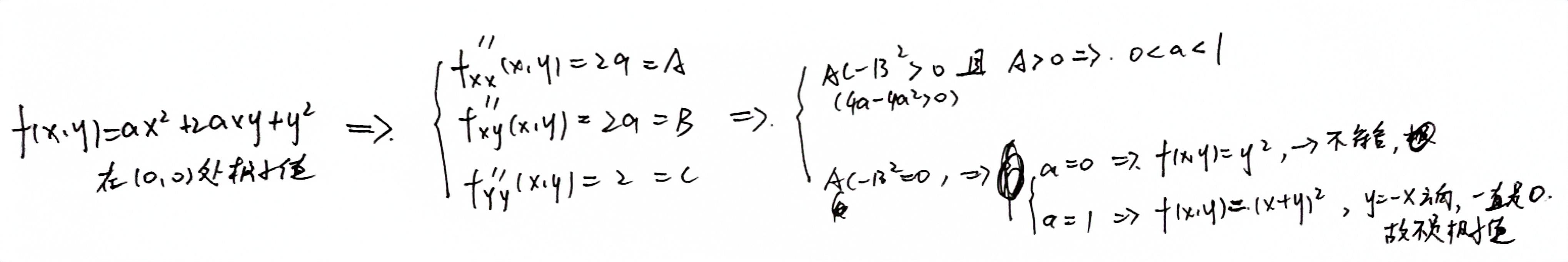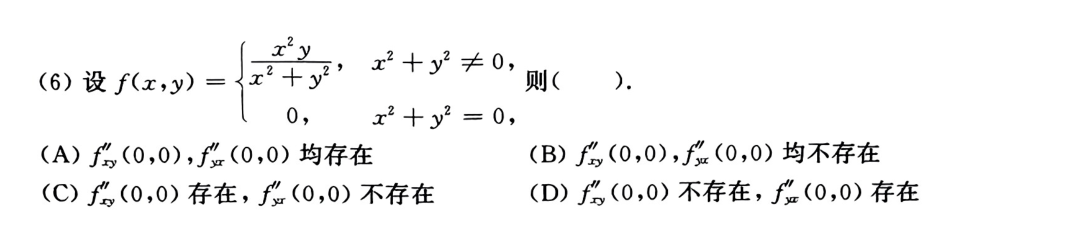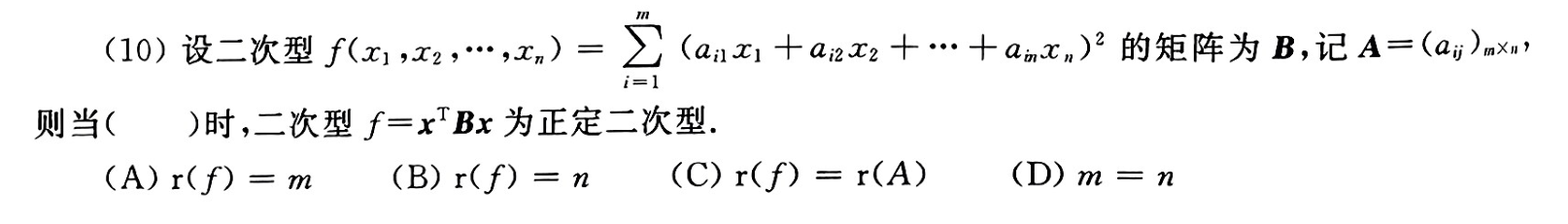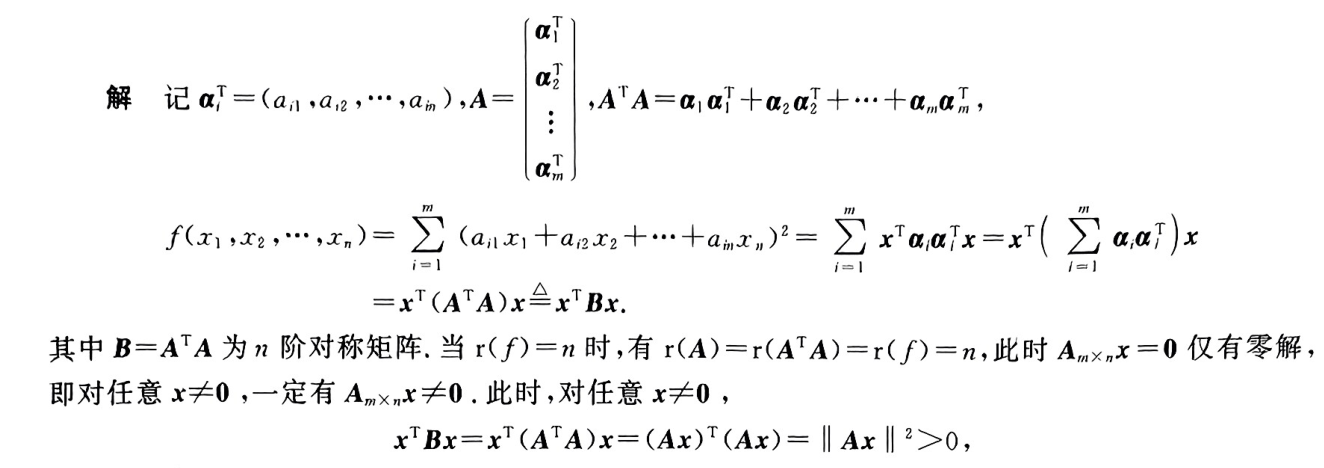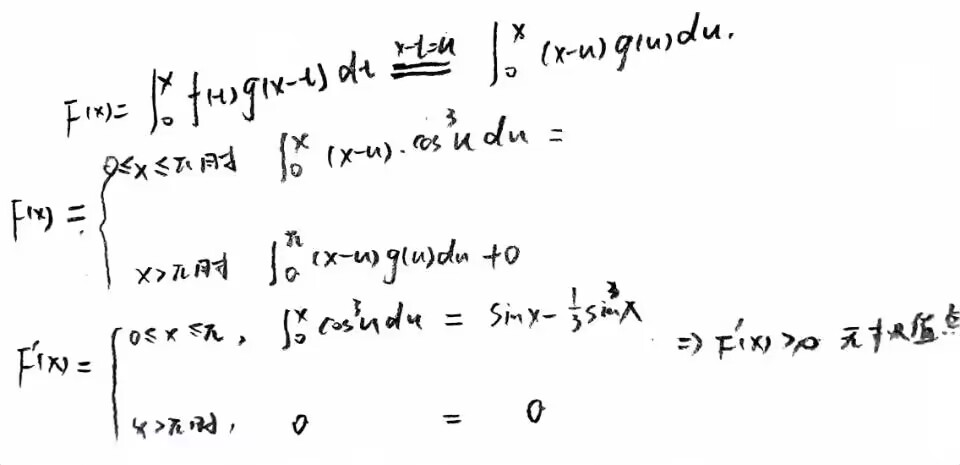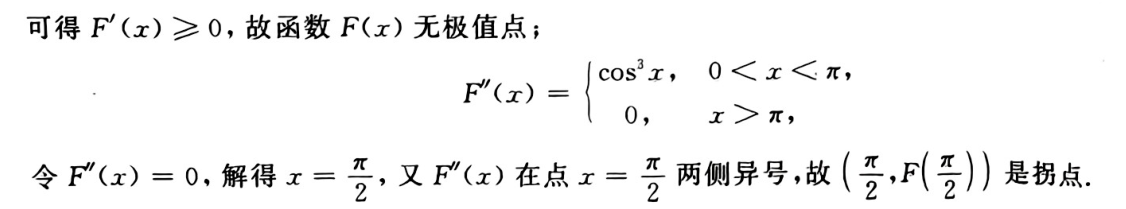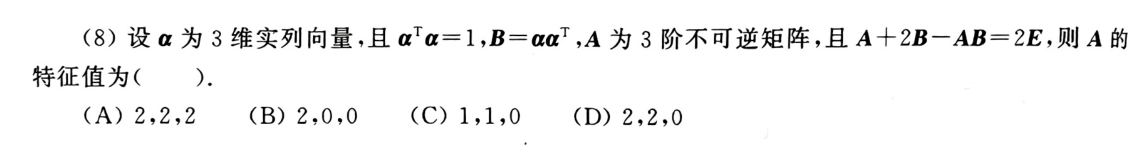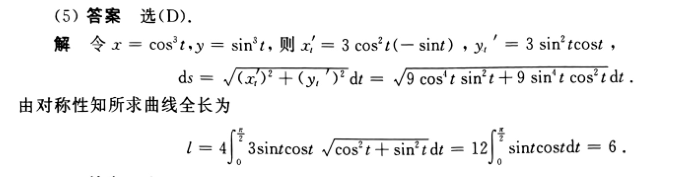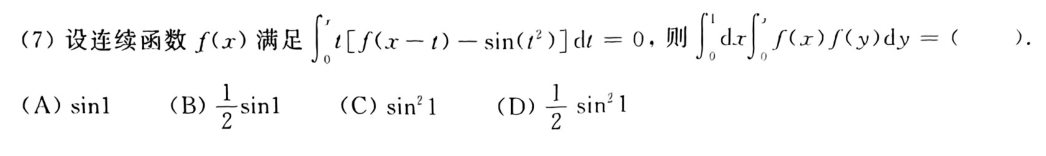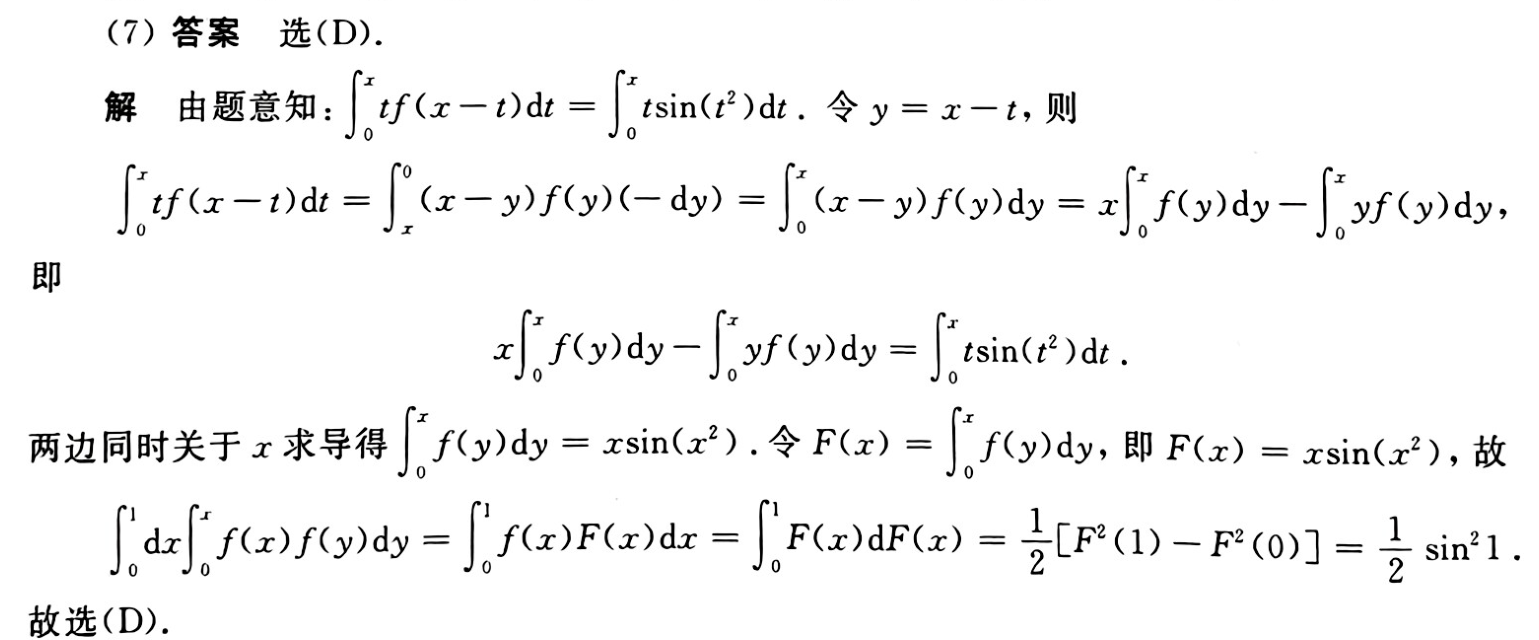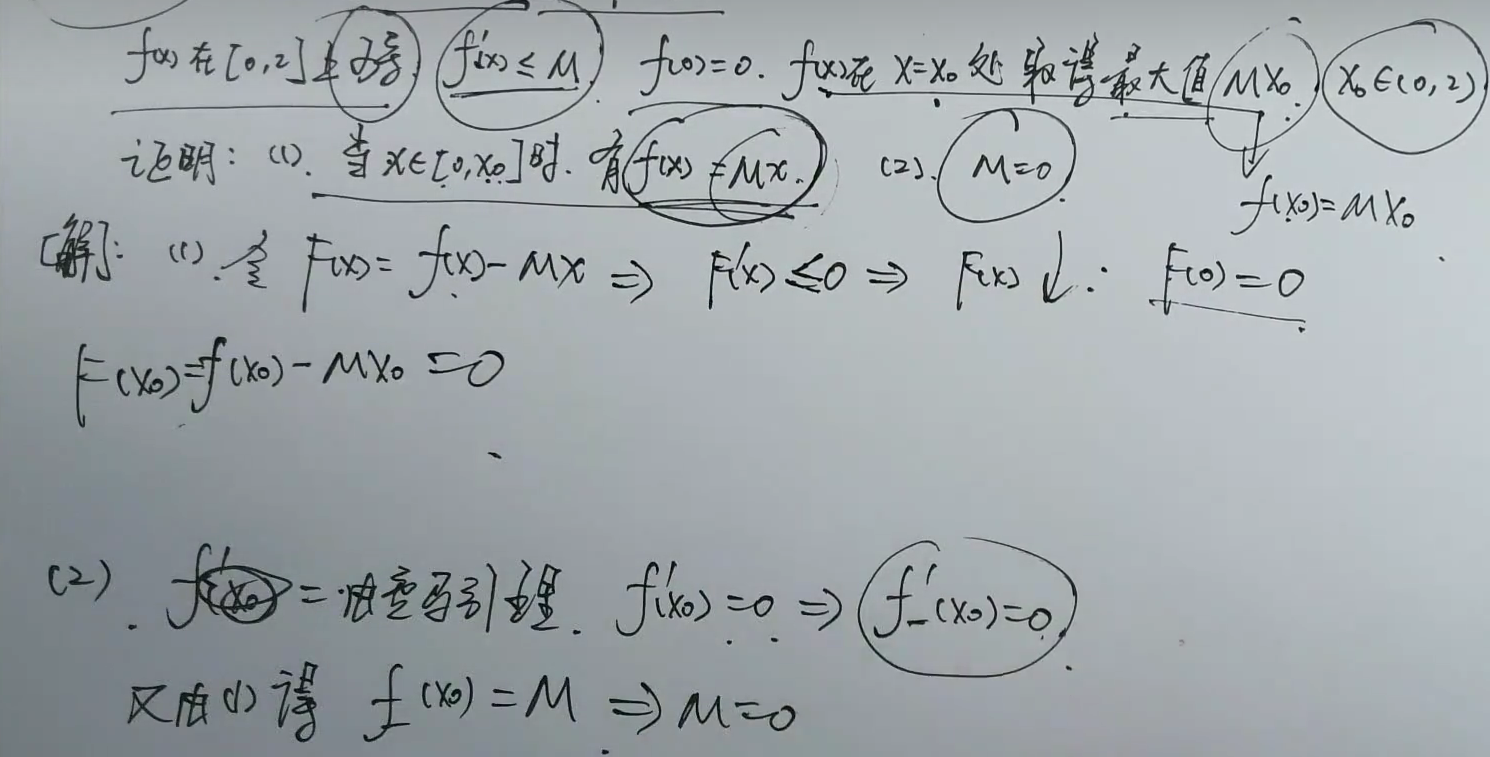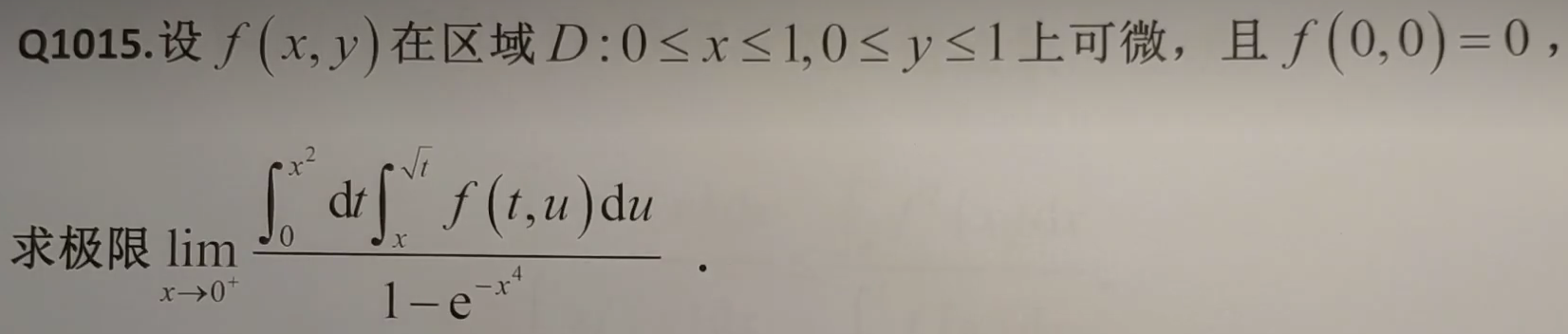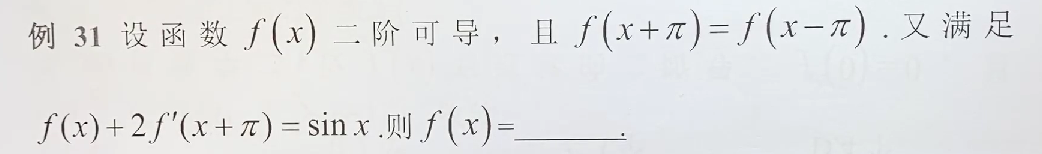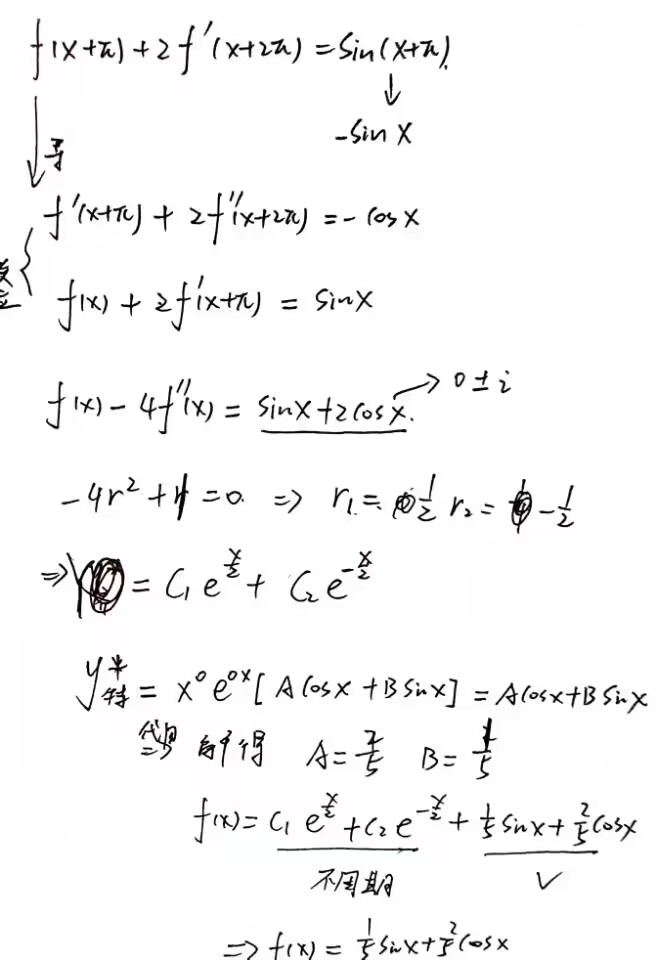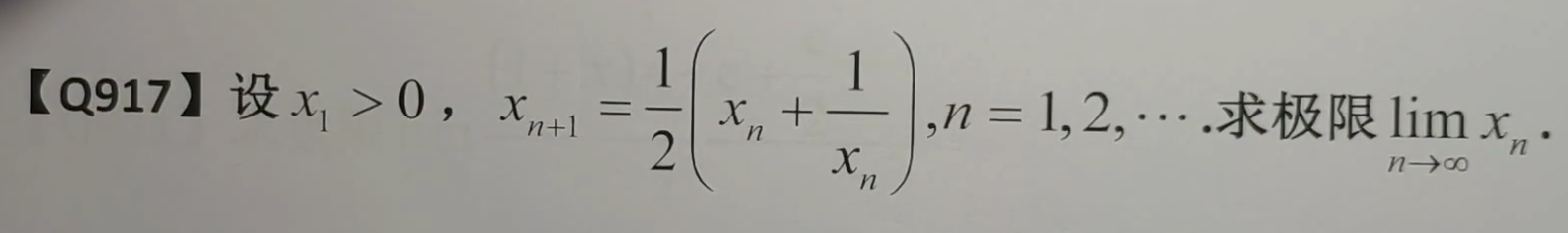高数题集

严选题

1.函数极限连续

选择题

开区间连续，两端点单侧极限存在，是函数有界的充分条件，而不是必要条件

相乘的极限存在，不想代表，各自都有极限

利用夹逼定理，单调有界准则

极限要求趋向于0，但不等于0，没有说明φ(x)不等于0

1.注意加减关系不能直接等价代换，等价代换实质上是一种精度不太高的泰勒展开(低阶展开)，当f(x)与g(x)存在加减关系时，例如这题是相加关系，如果f(x)与g(x)的低阶无穷小相互抵消(limf(x)/g(x)=-1),那么就需要比较高阶的无穷小；但是等价代换就没有高阶项，所以精度丢失- - ->
2.拆成两项极限求和的前提是–>两项极限都存在

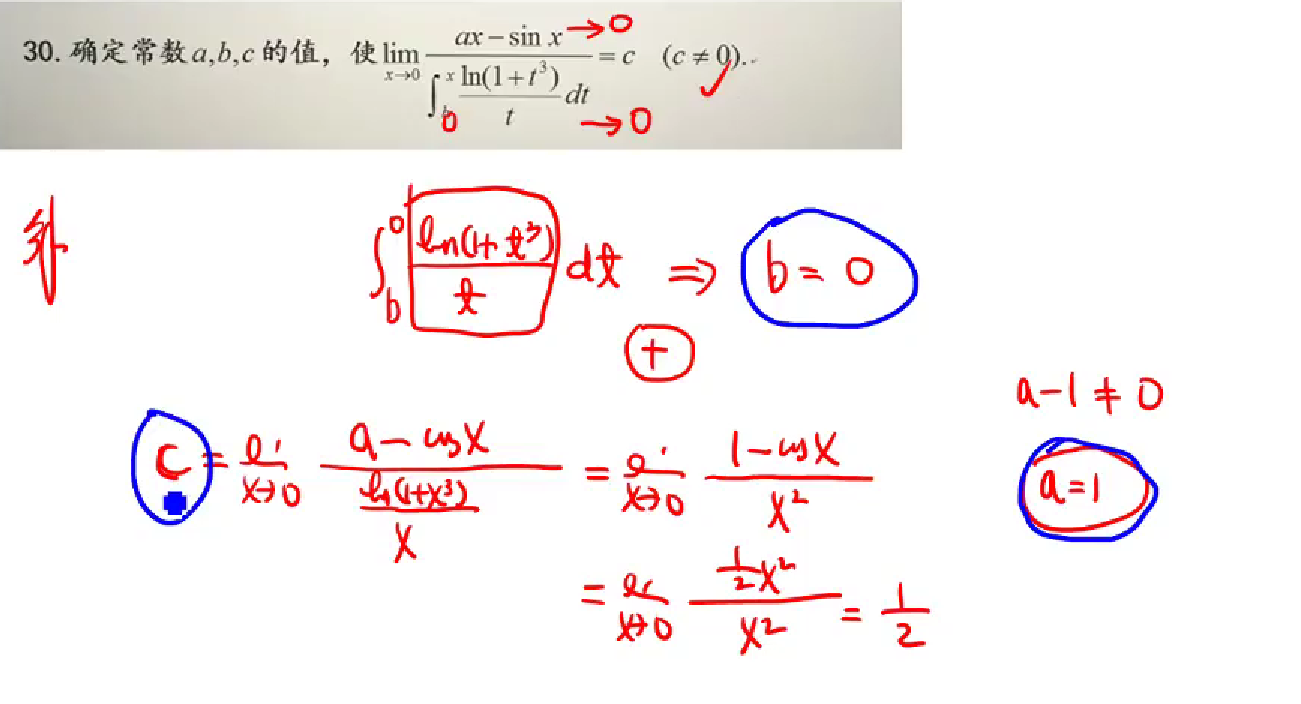
确定变上限积分函数，无穷小的阶数–>N(M+1)原则

1.当a=2,arctanx-sin2x可以分别等价代换，为什么？不是说加减不能等价代换吗？ –>等价代换实质就是一次低阶泰勒展开，当展开之后，最低阶的无穷小两者不相等时，意味着相减，不会消去这个低阶无穷小，就不需要比较高阶无穷小，那么就可以直接等价代换 ；arctanx-sin2x ~ x-2x

2.当a=1时，arctanx-sinx不能分别等价为x-x，因为低阶无穷小项，互相消去，需要比较高阶无穷小，但是arctanx的泰勒展开不熟悉，只能通过arctanx-x-1/3 x³ ,sinx-x -1/6 x³ ;

极限x->1不需要讨论1+,1-，因为极限保号性；同理x-> -1; 但是x->0,时，考虑0+,0-,因为两侧正负不同

最关键的还是，幂指函数指数化 来处理幂指函数

考察了基本极限x^n ,e^nx

填空题

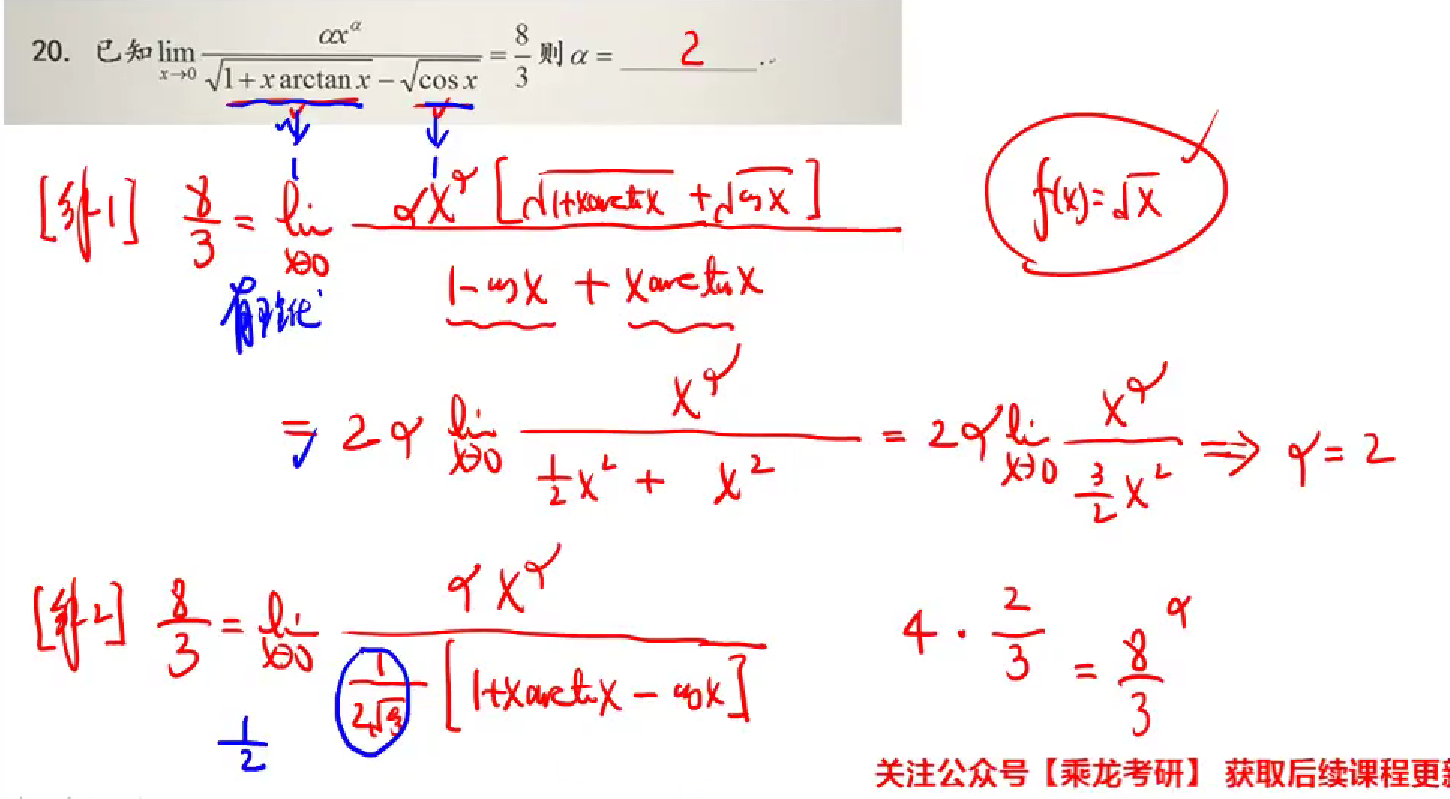
对于这种分母中含有两根号相减的，–>1.是有理化 2.是拉格朗日中值定理

考察知识点很综合
1.导数几何意义
2.基本极限求极限1^∞型
3.洛必达法则
4.变上限积分求导
5.导数的定义

ln(x+√1+x²) ~ x

1.利用到了ln(x+√1+x²) ~ x,判断时1^∞型
2.写基本极限标准型lim (1+a(x))^β(x) =e^ a(x)β(x)
*3.利用等价代换(1+a(x))^β(x) -1 ~ a(x)β(x) *

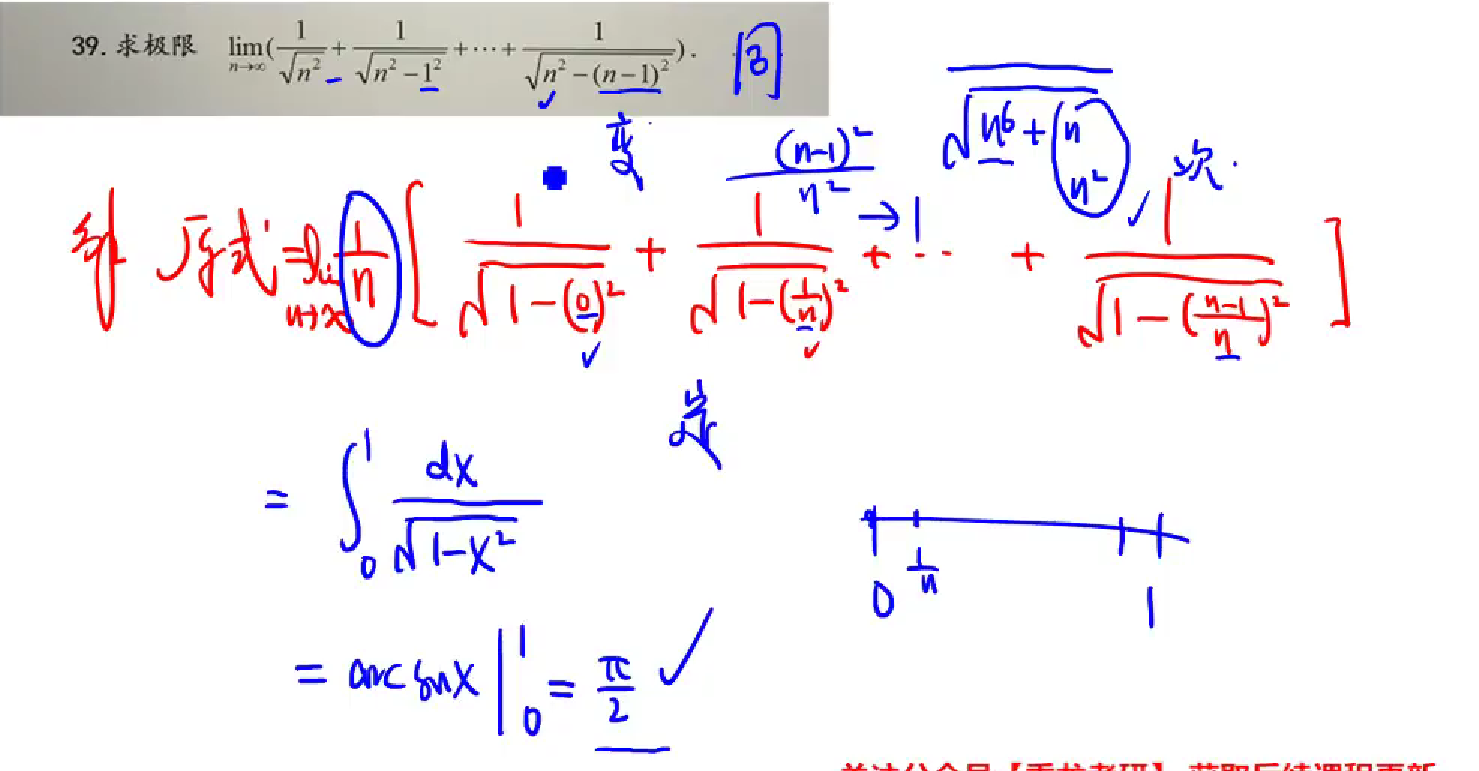
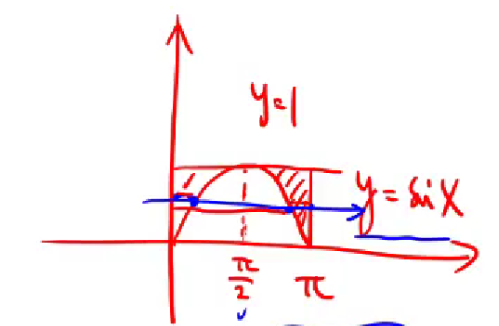
1.n项连乘 直接夹逼不出来，化为对数
2.关键再利用基本常用不等式
3.再夹逼

解答题

0/0型
1)洛必达法则
2)等价无穷小代换
3)泰勒公式

1.第一眼看，我想用1^∞型极限，但是这里不能拆开求极限因为，右半部分的极限不存在，所以不能1^∞极限直接做
2.正确的做法是将幂指函数，化为指数，然后将整个分子，e^x -1 ~ x等价代换

用到拉格朗日中值定理

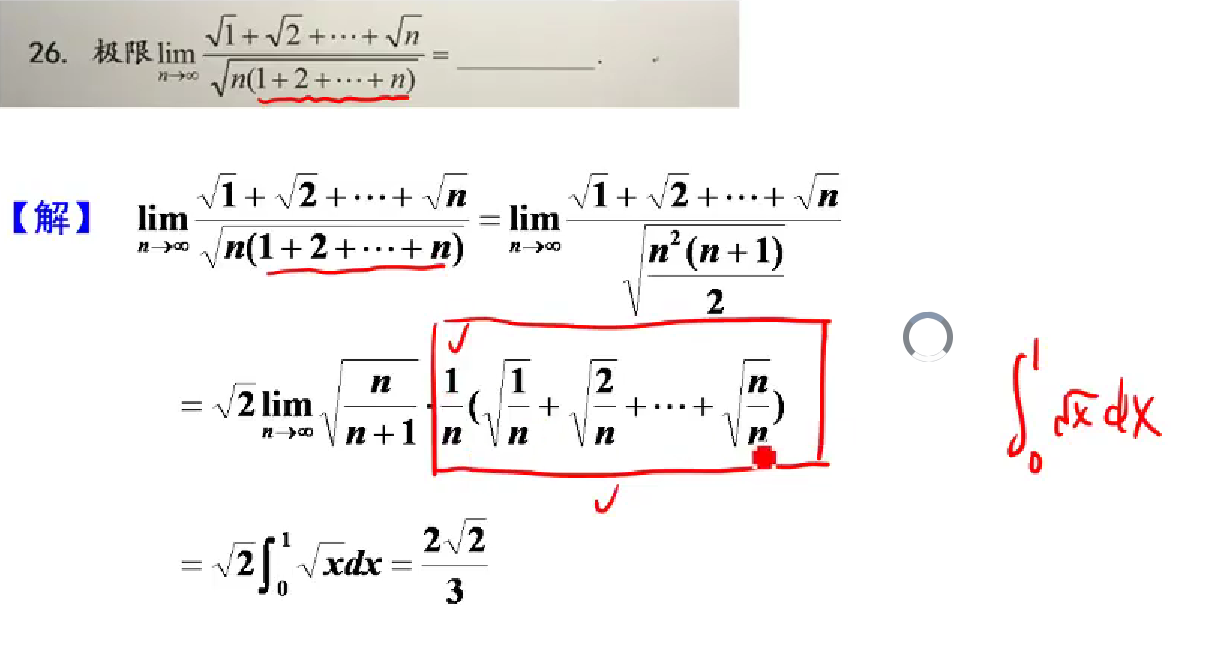
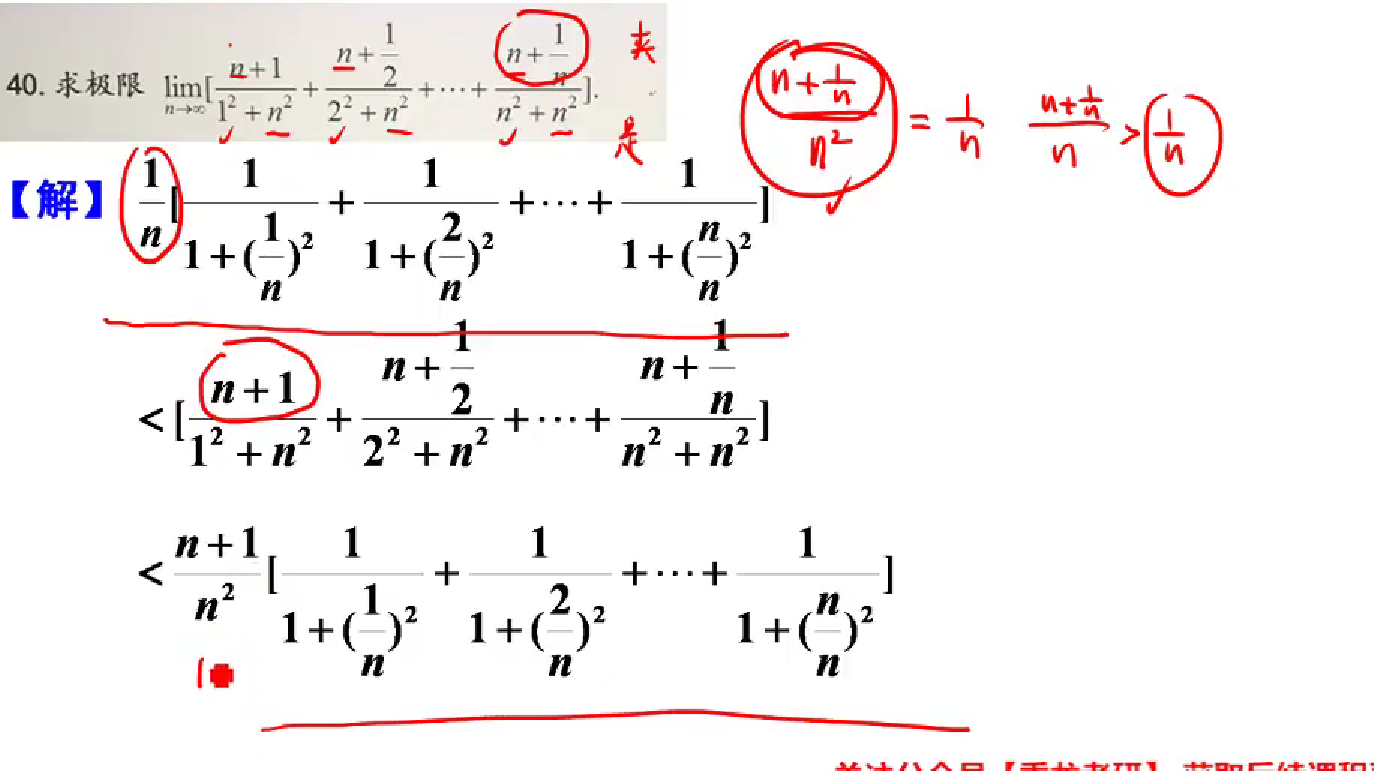
1.自平方项，前n项和，公式要记住
2.到底是选择夹逼，还是定积分定义，看每一项变化的那个地方，看是占大头(同量级，选择定积分定义)，还是小头(变化对分母整体量影响不大，用夹逼)

分子变化部分相对于主体是次量级，用夹逼；分母变化部分相对于主体是同量级，用定积分定义
对分子放大–>所有项分子=n+1/n; 缩小–>所有项分子=n+1
对分母提出1/n，可爱因子

经典的找间断点，和类型题目
在求间断点的极限时，是否要分开考虑左右极限，是根据，左右会不会对函数正负性有影响

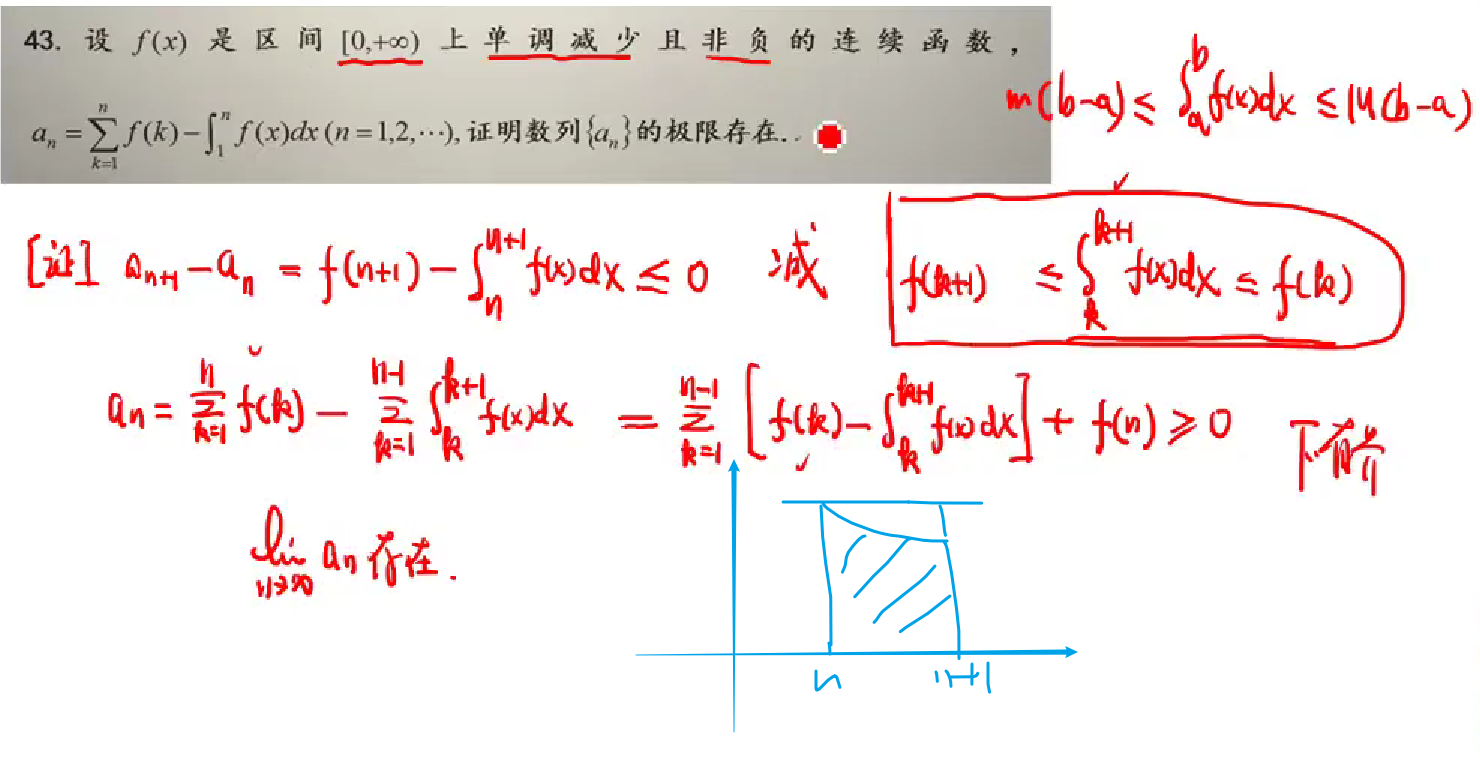
极限存在一般根据极限存在准则：
1.夹逼定理
2.单调有界准则
该题只需要证明极限存在，只需单调有界就可证明极限存在

1.先看递推式函数是否单调增
2.函数单调增说明数列有单调性，再根据x1,x2判断数列单调增还是减
3.假设极限=A，根据递推式代入A求出A
5.再证明有界且界限=A

1.先看递推式函数，是否单调增,如果单调减则数列没有单调性
2.接着没有单调性则，直接证明xn-√2的极限

零点定理–证明区间两端点异号，则区间内必有一点=0

介值定理–函数值介于最大与最小之间，必有一点,f(β)=该值

2.一元函数微分

填空题

既要趋近于0，又要同时趋近0+,0-，才能判定该点导数存在

考察连续的概念、导数的概念、导函数连续的概念

1.拆开求导。2.求得导数等于0的点，用二阶导数判定是极小还是极大

求得二阶导数=0，继续代入求三阶导数，看二阶导数是否单调，如果单调，那么该点就是拐点

*求斜或水平渐近线，直接将原式改写，为y=ax+b形式，利用x->∞极限求出a,b
*

填空题

不能用洛必达，没有一阶可导条件，并且数列不是函数，不连续

利用链导法，而不是将所有表达式求出来，再求导，那样太麻烦

反函数的导数，注意反函数是对y求导

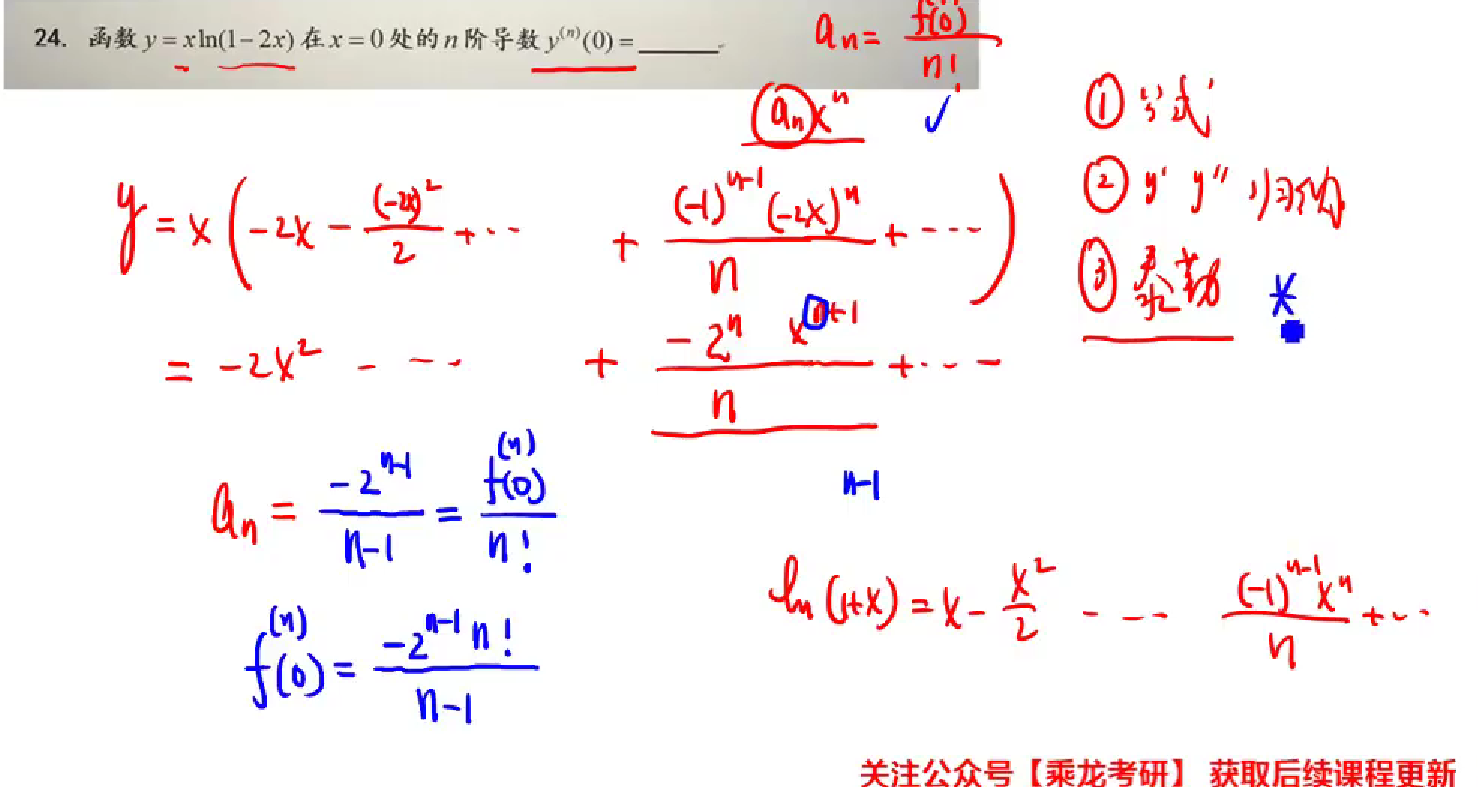
高阶导数具体点导数–用泰勒展开

求高阶导数–总结规律

根据罗尔定律

解一元三次方程=0，一般方法，凑1,2,3,4…整数

解答题

1.积分上限用变量代换
2.定积分定义求0点导数
3.求x->0，导数极限看是否=0点导数
4.运用到了积分中值定理

这种参数方程求积分问题，要注意变换积分上下限

单中值–微分中值定理证明题，主要是微分中值定理的构造

运用柯西定理、拉格朗日中值定理

双中值–两中值点没有要求不同
分开两部分

双中值–要求中值点不同
1.先将【0,1】段用c分开，假设存在一点c，使得…

证明中值，含有高阶导数–泰勒展开，在给出信息最多的那一点展开

3.一元函数积分学

选择题

原函数是否存在判定
1.函数连续，一定存在原函数
2.函数有第一类间断点，就一定没有原函数（证明：通过原函数的定义或者导函数的介值定理，F(X)在a,b可导，则其导数在[a，b]内不会有第一类间断。）
3.有第二类间断点，可能有原函数

直接判断导函数是否连续，如果有第一类间断点，那么原函数必定不可导

积分区域相同，比较被积函数，被积函数大，积分就大

旋转体体积问题

填空题

简单有理函数积分

对称区间，奇偶性判断

1.取根号，要注意加绝对值，分区间计算
2.善用结论

1.利用定积分定义，转化为定积分的计算
2.利用几何意义，想象为，一个半圆的面积的积分，直接求面积
3.也可以将x=sint，左变量代换

多项式分数，根式里面一次，一般变量代换

根式含有平方项，三角代换

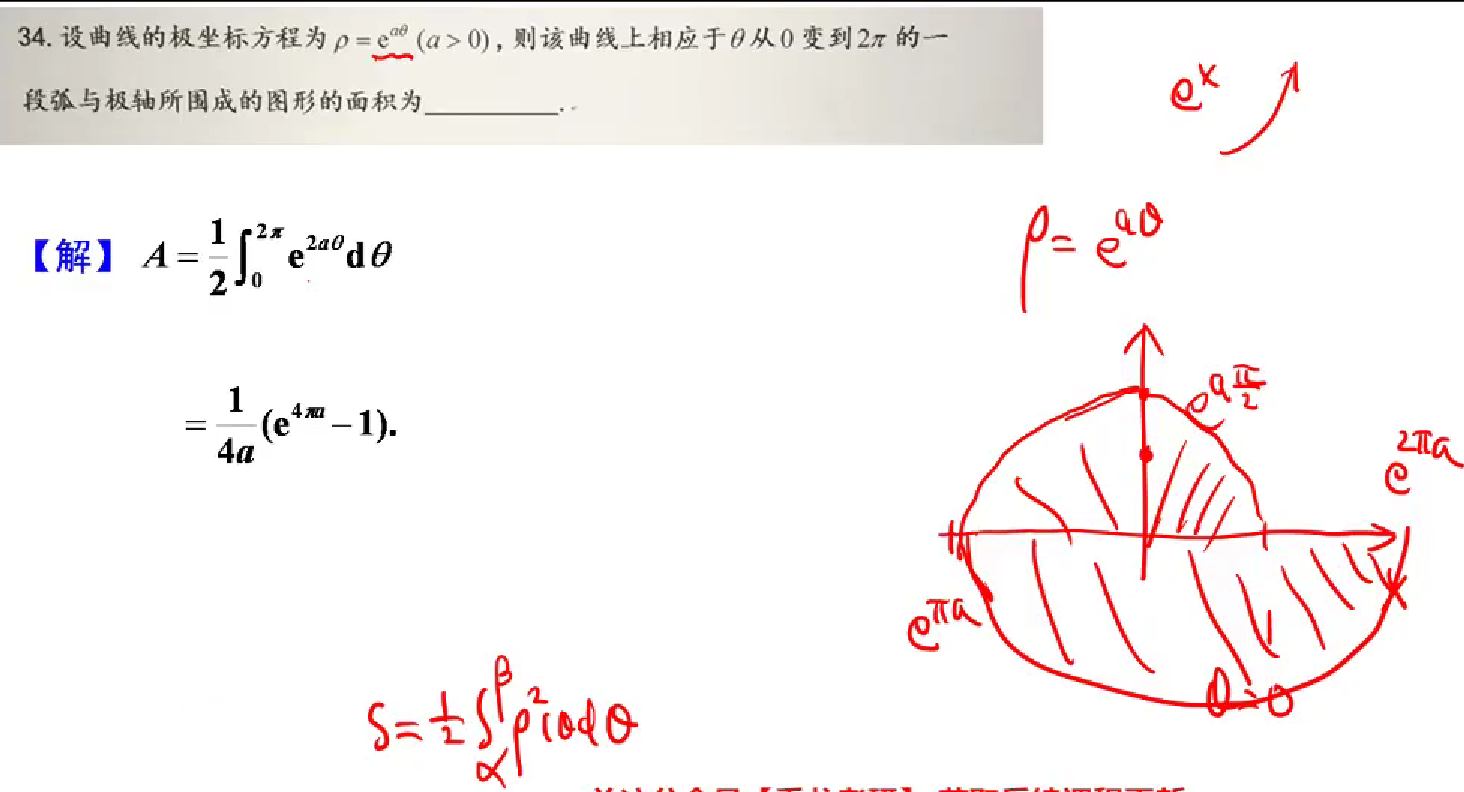
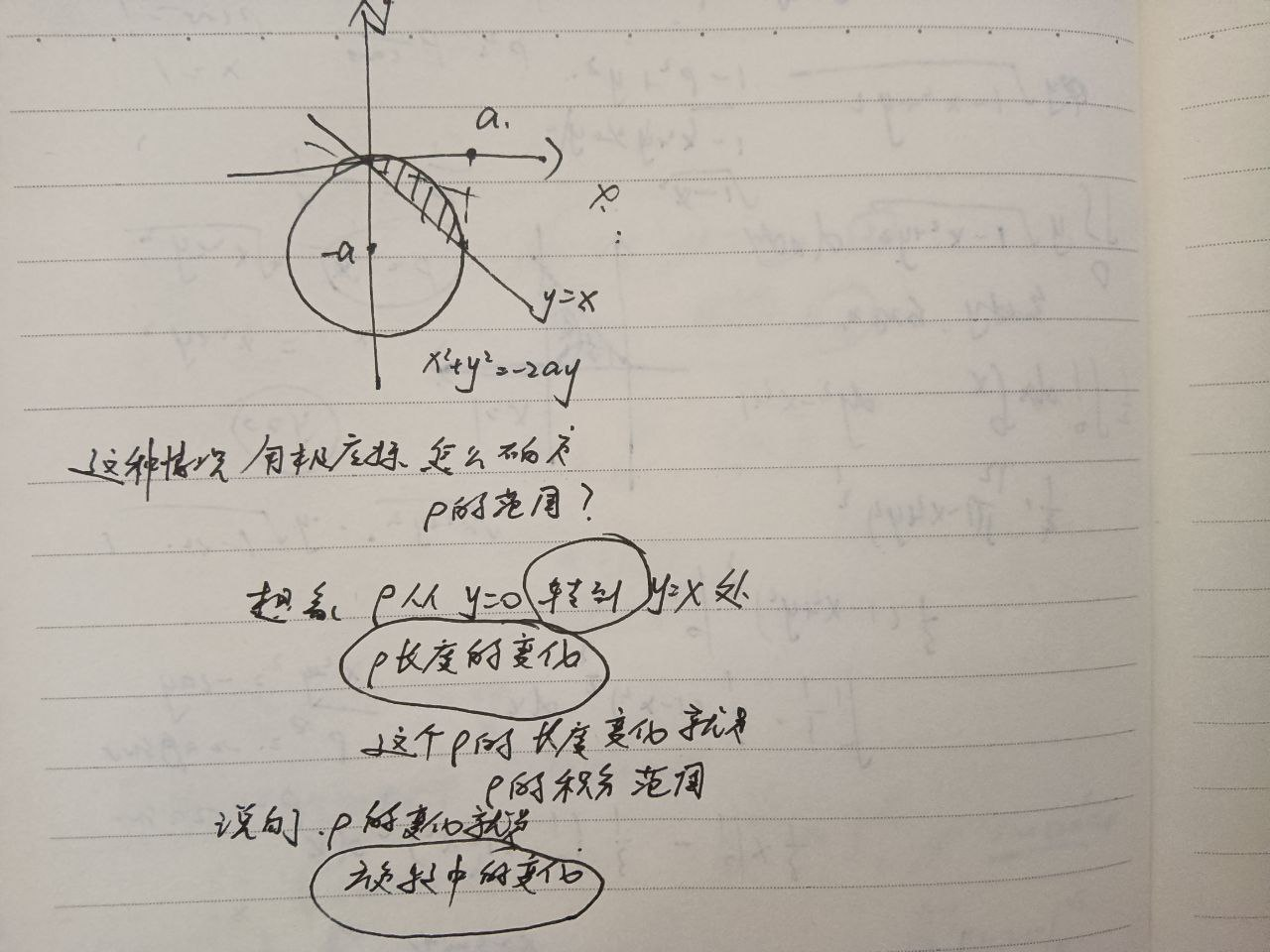
边界曲线，用极坐标给出，求面积的问题
可以直接套公式，
任然还有问题

对比着看

运用弧长积分公式

通过分部积分法，将f(x)写成导数计算

解答题

**

积分中值定理+介值定理+两次罗尔定理

方法1.利用介值定理，介于最大最小值之间

方法2.利用构造辅助函数，常规方法，然后再说明有两个点，辅助函数值相等(罗尔定理)，就证明等式成立

难题

长条中质心的积分计算公式

积分质心,又称质心坐标,它的计算公式为:

其中:

,  - 质心的坐标

,  - x方向的积分区间

,  - y方向的积分区间

 - x方向的积分函数

 - y方向的积分函数

这个公式表达了质心坐标是积分函数在对应方向上的质量乘以坐标的积分,除以整体质量的积分。

质心反映了物体的平衡点。利用这个公式可以计算出平面图形的质心坐标。

典型，积分求旋转体体积

4.常微分方程

选择题

直到三阶常系数齐次线性微分方程的特解，直接从特解中看出特征根，然后根据特征根写出特征方程，即可

非齐次解具有叠加性，可以拆开分析

填空题

解答题

1.三个线性无关特解，两两相减=通解
2.然后通过消去系数得到最终方程

不属于已知的类型，通过x,y对调,令y’ =1/x’,化为x为函数，y为自变量的函数

通过导数定义，构建微分方程

微分方程与全微分结合

5.二重积分

选择题

二重积分是一个数

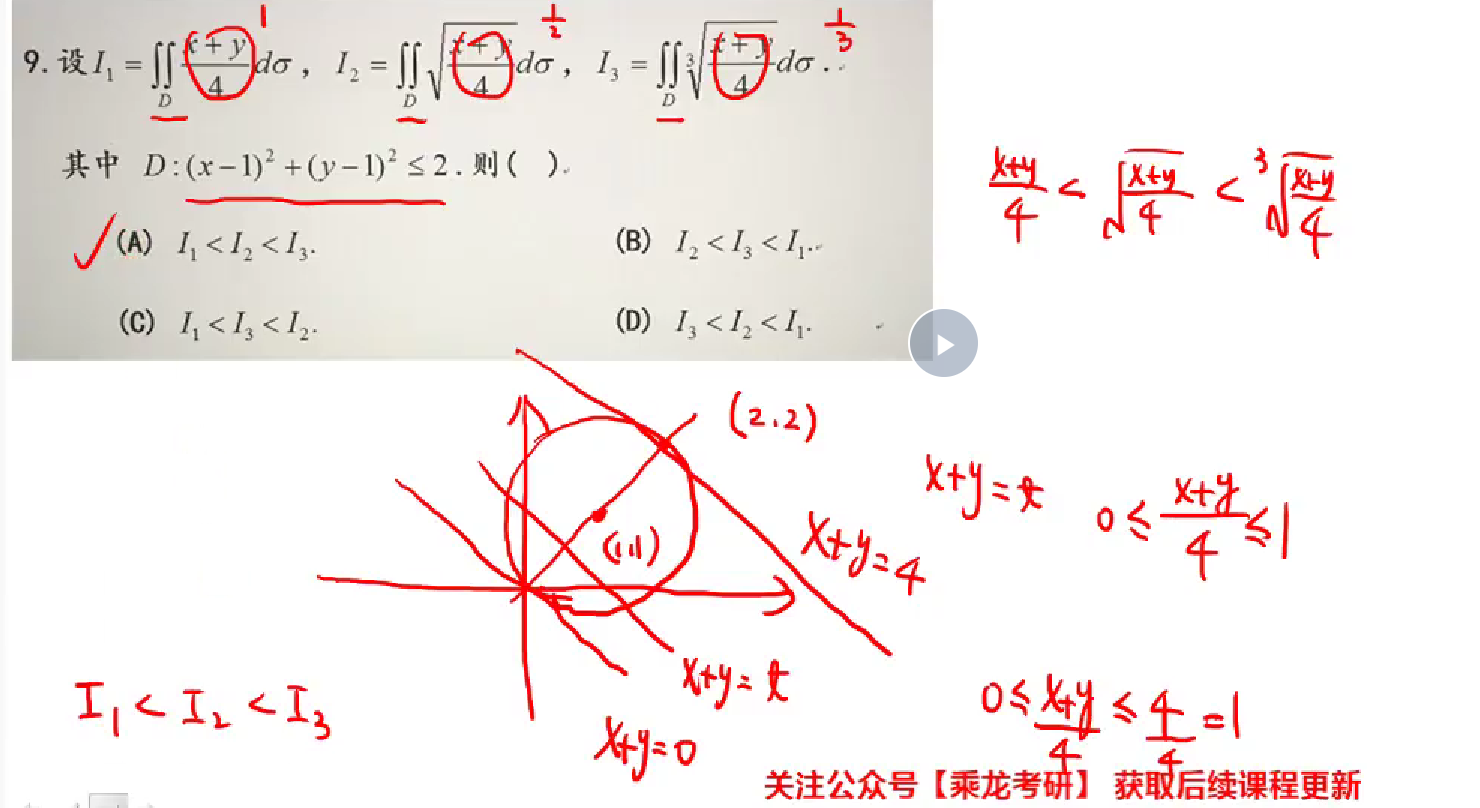
区域相同，比较被积函数大小

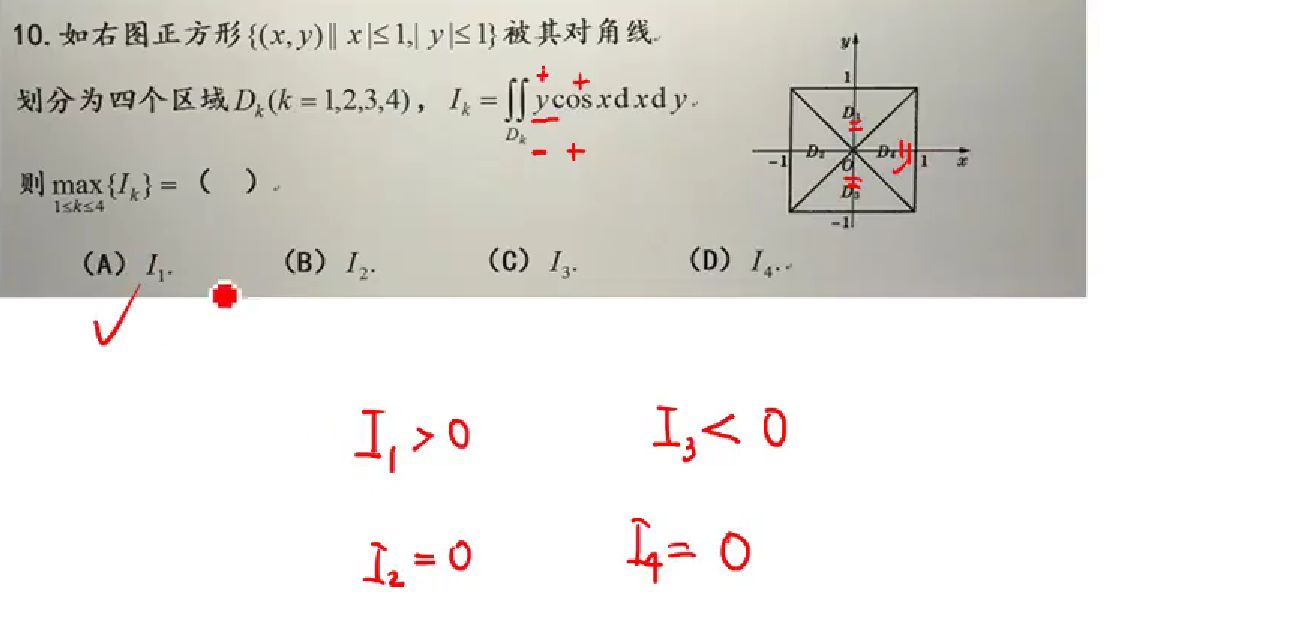
轮换对称性、奇偶性

经典

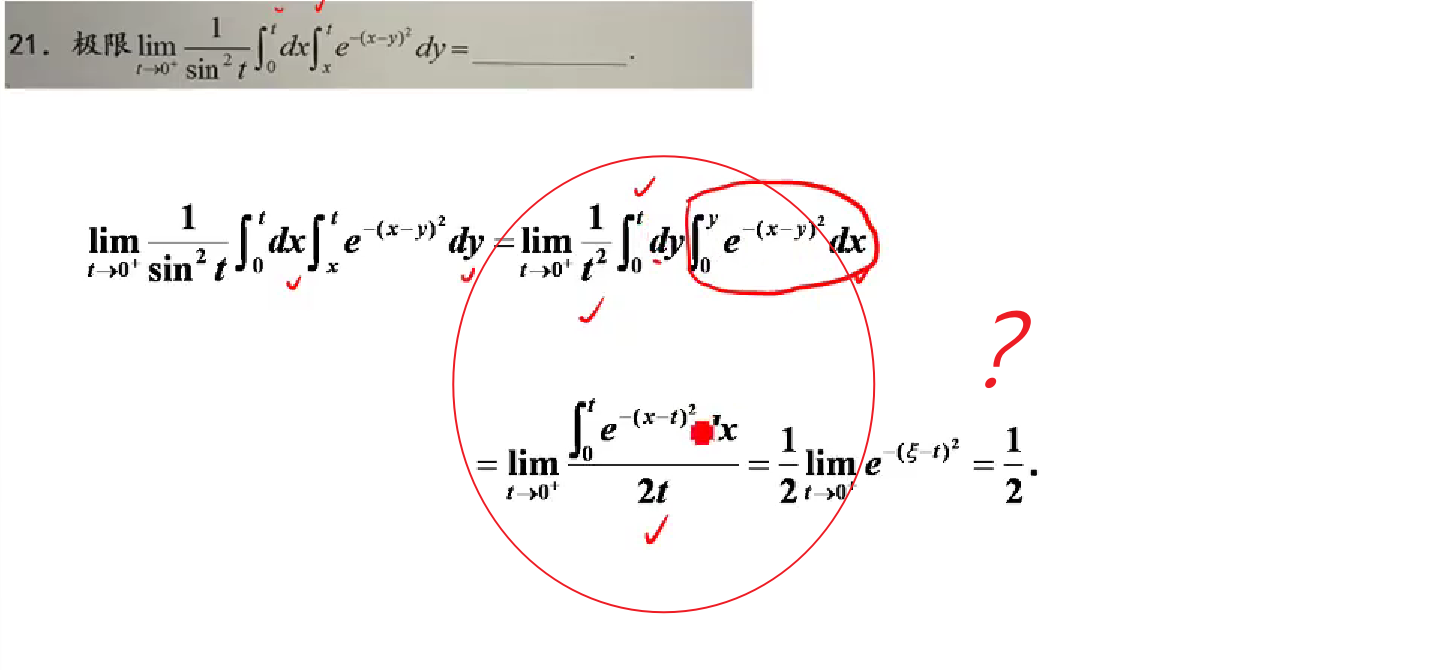
*累次积分对t求导
1.通过转换积分次序，使得只有外层积分保留t
2.将外层0~t积分对应微分的变量，在内层用t替换
*
例1

例2

例3

填空题

拆开、奇偶性、轮换对称性、极坐标法
太妙了

此时极坐标方便–>换位直角坐标，然后(x-1)关于(1,0)点的奇函数，利用奇偶性；最后计算简单

解答题

数列n项和，转化为定积分定义，最终得到一个累次积分

题目给的积分不好积分，就交换积分次序
1.先画域
2.重新确定积分次序，就可以简便积分

该题很有规律，不要硬算，算不出来

没想到的，极坐标不好用，换成极坐标

利用奇偶性、对称性

圆形不再原点的，通过平移，使得圆心在原点

注意奇函数乘偶函数=奇函数

积分的绝对值<=绝对值的积分

6.多元函数微分学

选择题

求偏导数

D.正确
从x方向趋向于x0,的极限，而y0固定的，相当于一个一元函数从x方向的一元函数，由于x方向的偏导数存在=a, 再根据一元函数可导必定连续，说明该函数极限就等于函数值f(x0,y0) ;同理y方向趋向于y0极限也存在也等于f(x0,y0)

1.首先证明偏导数存不存在(用定义法)
2.判断出两个偏导数都存在，接着通过可微判断式，判断是否等于0
3.最终式子如下，利用y=kx（其中一个方向趋向于y0）,看极限手否与趋向的方向无关(也就是如果极限与k有关，那么极限就不存在)

偏x方向导数>0,所以延x方向是增加的，同理延y方向减小

极限保号性，既然当x->0,y->0时 f(x,y)>0, 且f(0,0)=0,所以f(0,0)就是极小值

AC-B^2 <0 所以内部无极值点，那么由于这是一个有界区域，所以最值位于边界上的点

填空题

知道偏导，求函数本身–>偏积分法

*公式法，将x,y,z看做独立的变量，而不用再将z看做x,y的函数

解答题

AC-B^2=0，不能确定是否有极值，需要通过定义判定
1.极值的定义是，一个极小区域内无论函数从哪个方向趋向于极值点，函数值都是要么都同号，不会有正负都出现的情况
2.所以分别从y=x方向与y=-x方向趋向于(0,0)点，发现两个方向趋向于该点，一个方向值为+，一个方向为-，就说明该点不是极值点

我做错了

数形结合，起始就是求z坐标绝对值的最大值，由于|z|不好求，所以改为求z^2

1.利用齐次方程，有非零解时，系数行列式=0的特点
2.求长半轴与短半轴长度之比，实际就是求椭球距离原点最长最短距离之比

把证明不等式的问题，转化为证明一个条件下，最大最小值的问题

7-无穷级数

选择题

(1)好理解
(2)采用比值法，需要取极限，而不是单单相除，例如(1/n+1) / (1/n) <1 但是取极限就是=1，而1/n级数是发散的
(3)比值法，前提是两个都是正项级数
(4) 0<=bn-an<=cn-an ;与都收敛，所以收敛
大收则小收，bn-an也收敛，因为bn = (bn-an)+an,两个收敛相加依然收敛，故bn收敛

关键：级数与函数有关，函数连续，想到函数必定有界，设M

A. an->0,所以anbn<bn ,大收则小收，但是不确定bn是正项级数还是有负的

填空题

*级数是等价于,是发散的，
原级数看做是逐项求导，收敛半径不变。
将x=0代入，是条件收敛
又因为幂级数条件收敛的点只可能发生在收敛区间端点，所以0是区间一个端点，所以收敛半径=1；收敛区间（-2,0）

我的方法是直接代入，x=3,-3(根据直觉)，发现x=-3时条件收敛，那么x=-3一定是收敛区间端点，接着就能找出收敛域

解答题

考察对各类级数敛散性判定

x的范围一定要写，原公式-1<x<1

像是arctan，的幂级数展开，一般是求导，展开，再积分
积分是要变上限积分

省略二次求导，再积分

这种题，和函数的导四次，回到原来的和函数，建立微分方程，求解
【注意通解中含有4个变量，需要四个函数值，0! =1,所以y(0)=1,y’(0)=0….】

求常数项级数的求和，借助幂级数，写成常用的展开的形式，再代入x=1（这题来说代入x=1,恢复原来式子）

这种微分方程不好解，那只能代入方程，将x化为同次幂，关注其常数项系数=0，就能找出幂级数系数的关系式

与上面一样的做法，将x化为同次幂，找幂级数系数的关系

S’(x)，和函数的导数，这个导数幂级数要从n=1开始，因为n=0的项是常数a0,求导之后没了

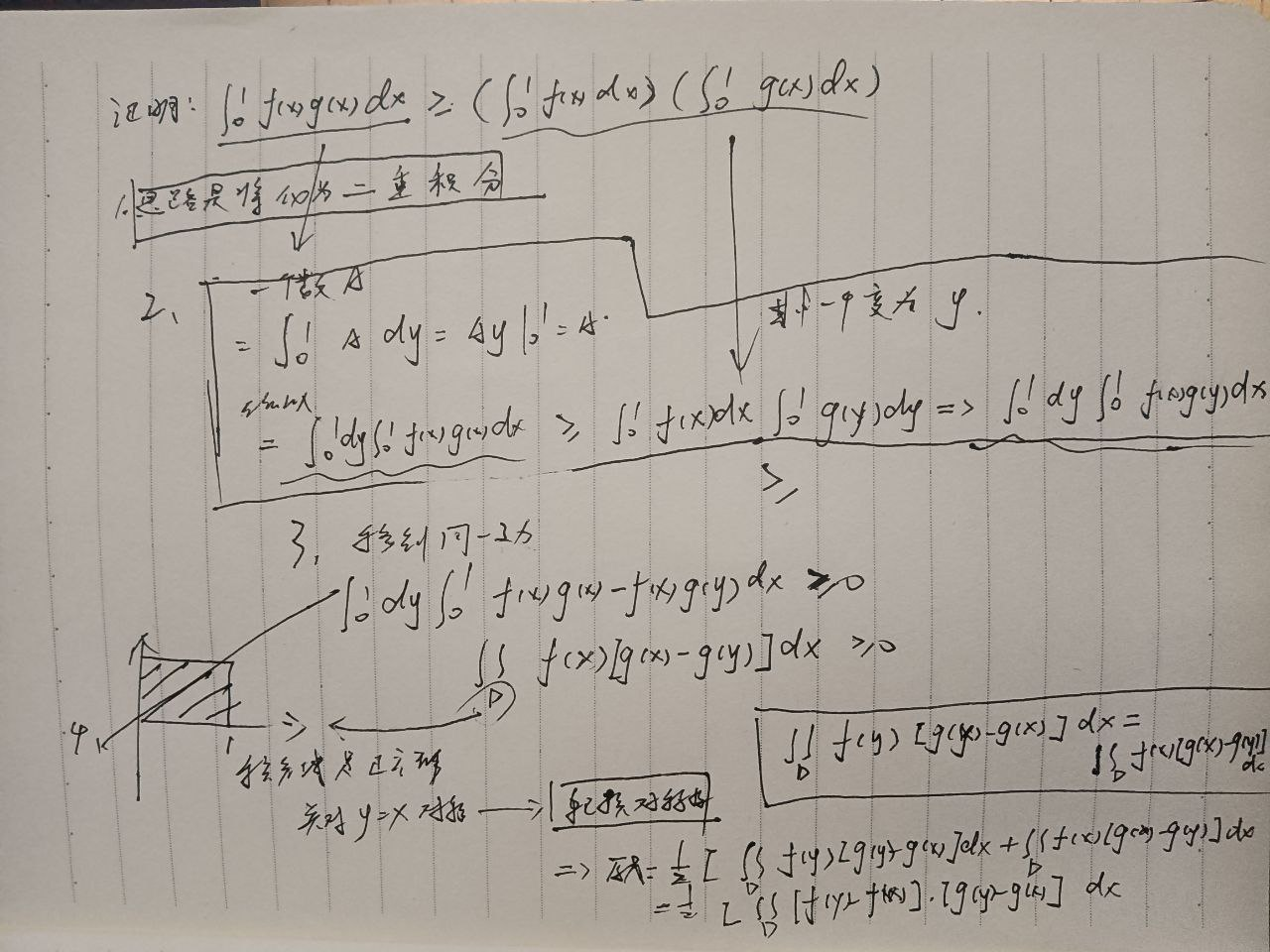
运用到了柯西积分不等式

傅里叶级数展开的系数问题

8-向量代数与空间几何

选择题

直线L2由两个平面相交给出，；
1.求出两条直线的方向向量，【L2,方向向量，由两平面法向量叉乘得出】
2.方向向量知道，就能求出余弦

曲面和平面的法线都是将函数写成F(x,y,z)=0,的形式，法线向量坐标都是对x,y,z求偏导

梯度计算

填空题

混合积有轮换对称性质

解答题

方向导数最大时，就是延梯度的方向且方向导数的最大值是梯度的模

投影直线绕某坐标轴转所得到的旋转面的方程

直线L的方向向量是(2,1,-1),而不是(2,1,-2)

根据两面写出平面束方程（经过该直线的所有平面），然后利用平面法向量垂直于该直线方向向量

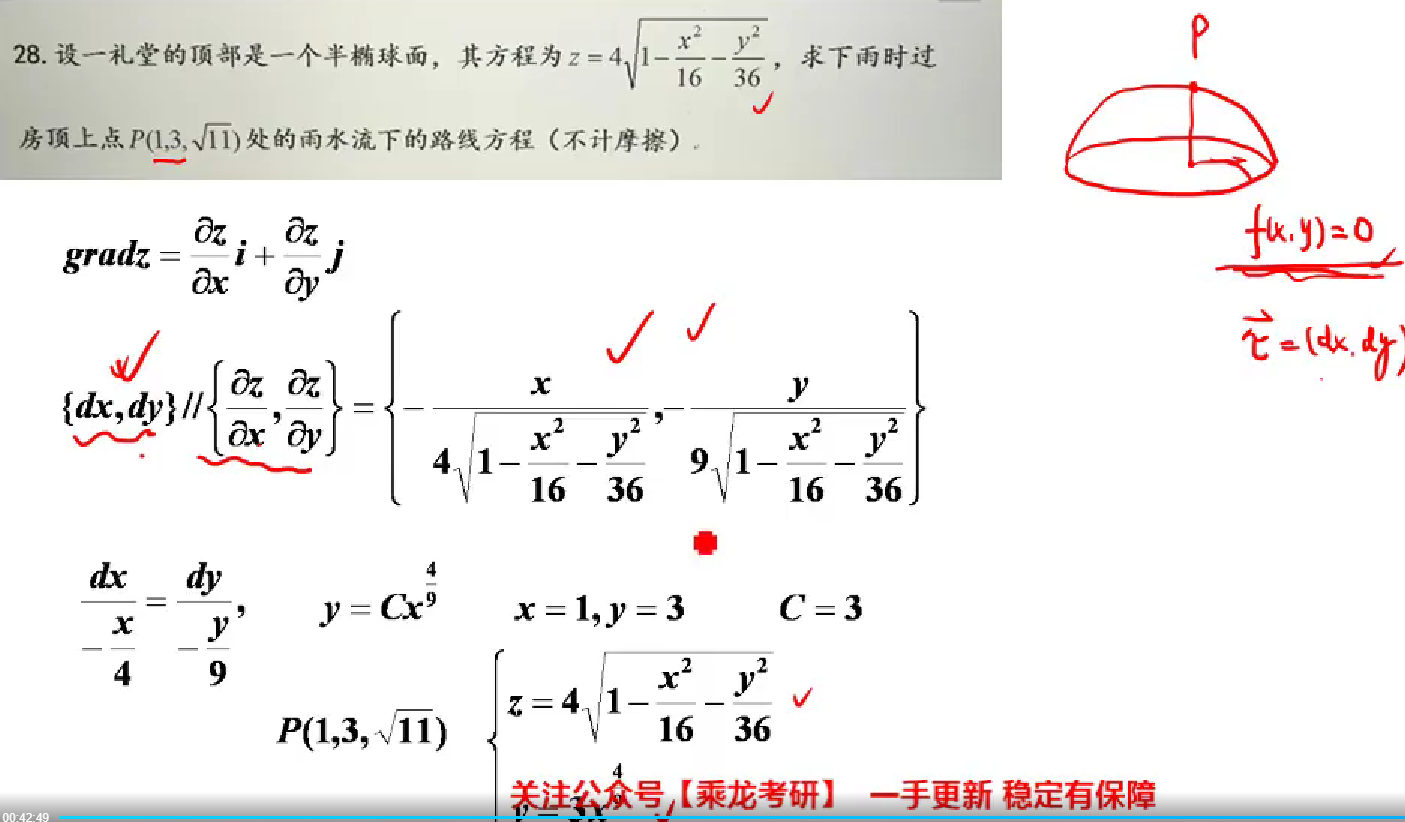
梯度向量是空间曲面在平面上的投影的水平方向的向量
这题就是利用了水滴会延梯度向量方向(平面向量)流动，并且流动轨迹xoy面投影的切线向量就是梯度向量方向
解微分方程，求出了投影曲线的柱面方程，联立球面方程，就是路线方程

9-多元积分的应用

在竖着的椭圆内是正的，在外边积分是负的

这题，先拆开利用奇偶性，消去部分项，然后，分别对三项积分，只积分其中一项，(中间利用椭圆面积=πab),然后推出其他两项的积分

画出积分域，交换积分次序

我做出来了

**

这题是对空间平面的积分，一般有几种方法：1,斯托克公式，2.化为一维平面(降维)

形心计算公式

严选题refine

1.

思路：

---

2.

思路：夹逼得到两个极限，不行，所以利用基本不等式

---

3.

思路：

---

4.

思路：==

---

5

思路：夹逼，平方项和公式

---

6

思路：夹逼+定积分定义

一次夹逼就可以了

---

7？

思路：利用罗尔定理，
令，根据罗尔定理至少有n-1个驻点

---

8

思路：多次项的方程的重根的那个点，就是驻点
心得：求多次数的方程的解，先猜出其中的解常常有1，2,，-1，-2,然后再根据已有的解假设最后的解a，构建因式还原方程(x+1)(x+2)(kx+a)，最终就能解出所有解

---

9

思路：

---

10 设且证明

思路：

---

11

思路：，

---

12

---

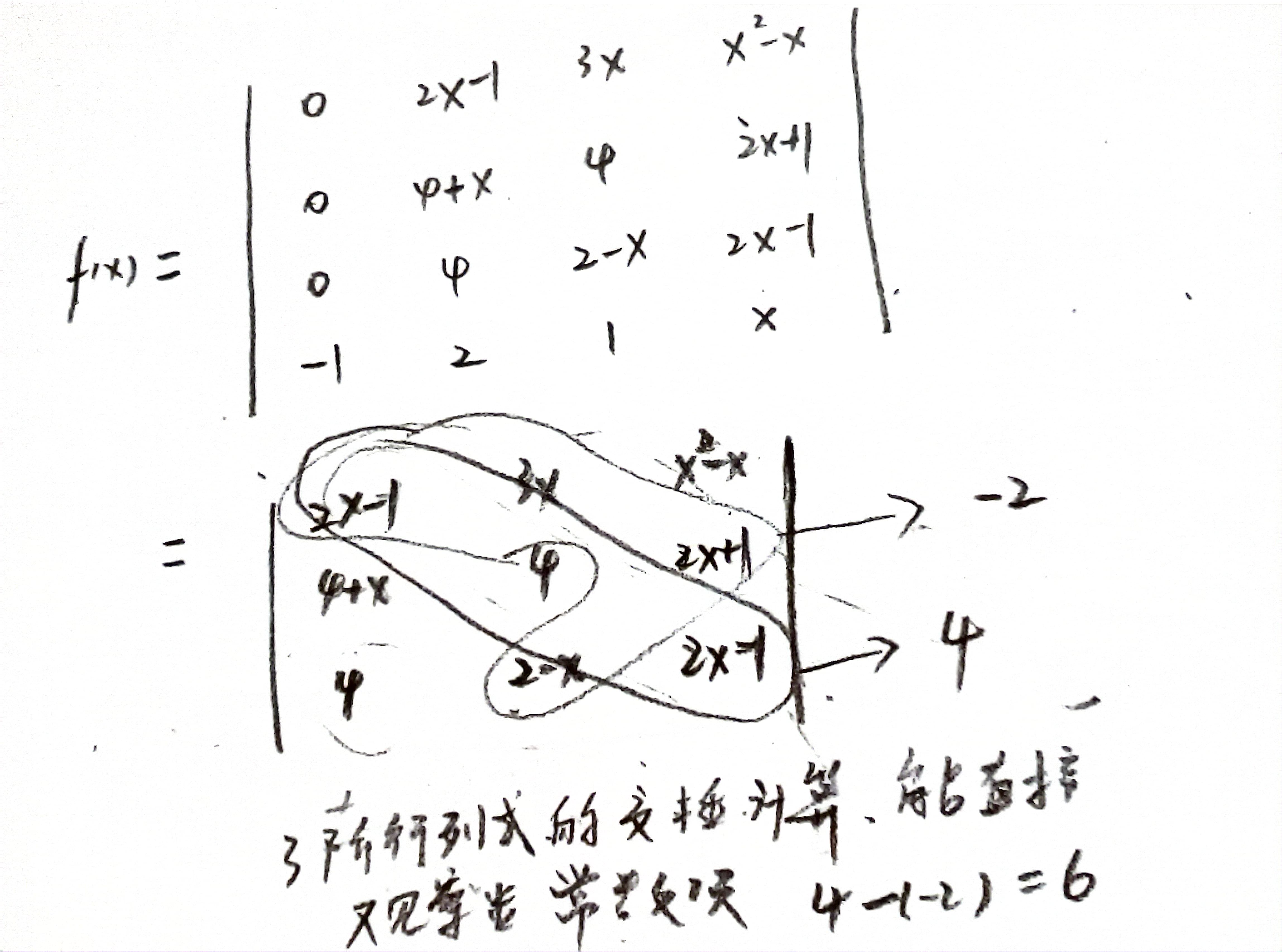
13求

思路：原式

---

14

注意：原函数在x=0处，左右导数都存在且相等，该点可导，所以原函数在x=0处必定连续，在确定常量C时，要注意原函数的连续
例：

---

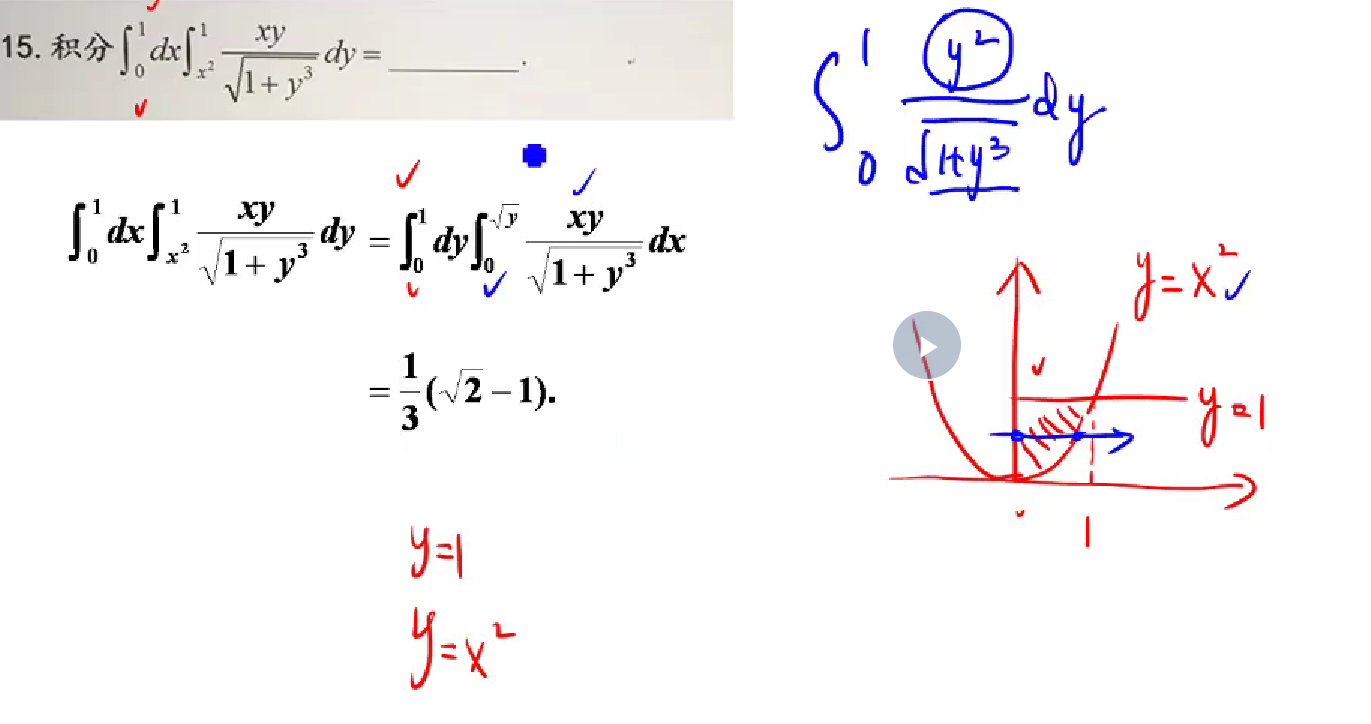
15

思路：首先想到对f(x)左变量代换，但是得到的是sinx/x的积分积不出，换个方向，例如对分部积分，

---

16

思路：第一问好证，利用积分中值定理。第二问，构造函数,积分上限将b作为变量。结合第一问的结果，结合f(x)单增，就可以做出来

---

17

思路：

---

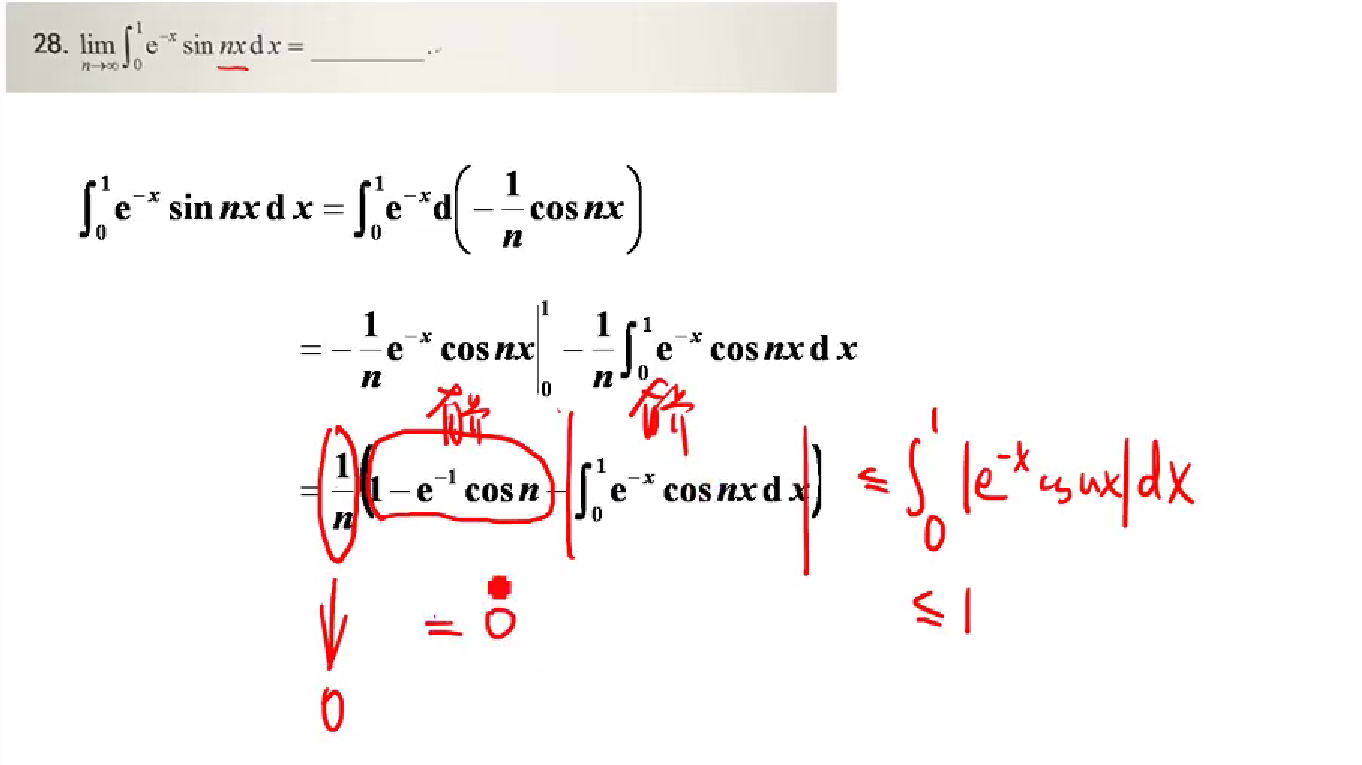
18

思路：
接着求n极限就行了,结果=0

---

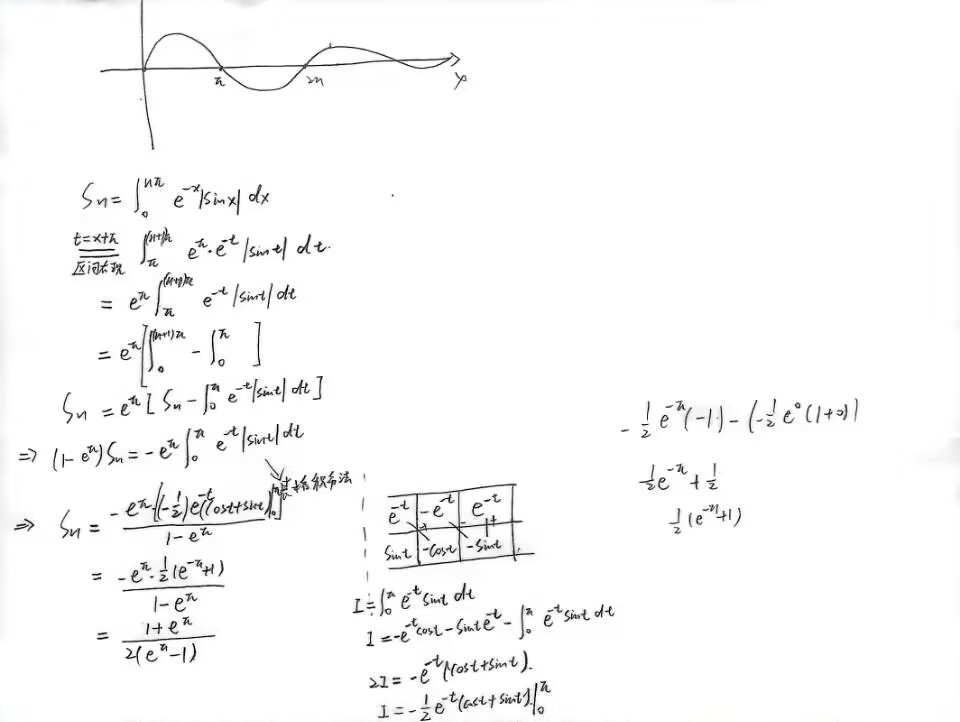
19

思路：

---

20🥝

思路：
（1）题目的暗示已经很明显了，等式左边

（2）
所以
…结果=1/2

---

21🥝

思路：

---

223阶常系数线性齐次微分方程
【例8】(2010年2)的通解为

思路：

r1=2；r2=r3=±i

【注意：有三个解时，r1不算是单根，所以按照双根的公式，r2,r3按照虚数解的公式】

---

23

思路：
注意这里丢解了，起始u=±1是解，取u=±1

---

---

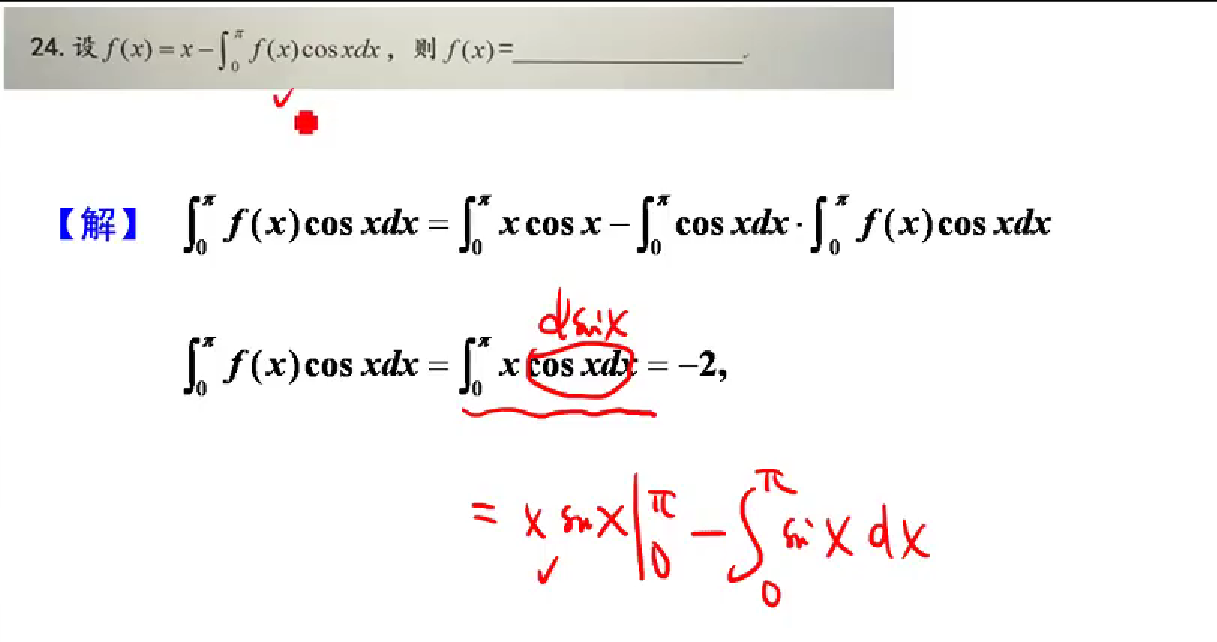
24

思路：求的是高阶非齐次的特解，按照特解公式求解。【这里的非齐次f(x)可以分为两部分，f(x1)=；f(x2)=；所以这是个叠加的特解，要分别算】

---

25

思路：

---

26

思路：f(x,y)=C 是一条直线，那么=0

---

利用保号性

---

分析过程
1.根据条件呼出区域D
2.分析区域内部与边界，分别分析。令俩偏导数=0，得驻点位于(0,y)、(4,0)、(2,1),只有(2,1)是区域内驻点，且是唯一驻点，那么在区域内(2,1)必定是极大/极小值
3.再讨论边界上的点，求得x=0时，z=0 ; x=4时，z=-64 ;
4.结合z(2,1)=4, 函数区域与边界是连续的，所以最大值=4，最小值=-64
这题的限制条件是直线，所以很好将y用x换，可以不用拉格朗日数乘法

---

29🍋

思路：

AC-B^2=0，不能确定是否有极值，需要通过定义判定,一个极小区域内无论函数从哪个方向趋向于极值点，函数值都是要么都同号，不会有正负都出现的情况

不同号，所以（0,0）点极值不存在。

---

30

思路:

---

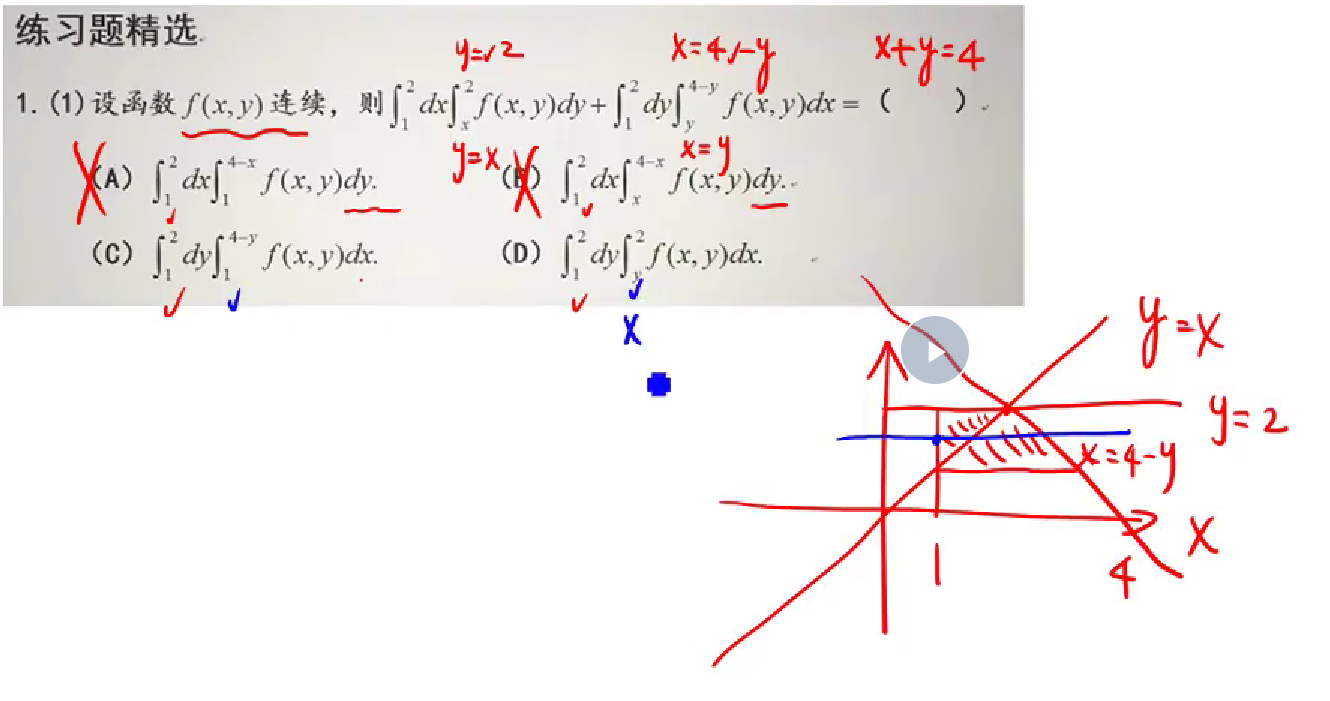
·31

答案：

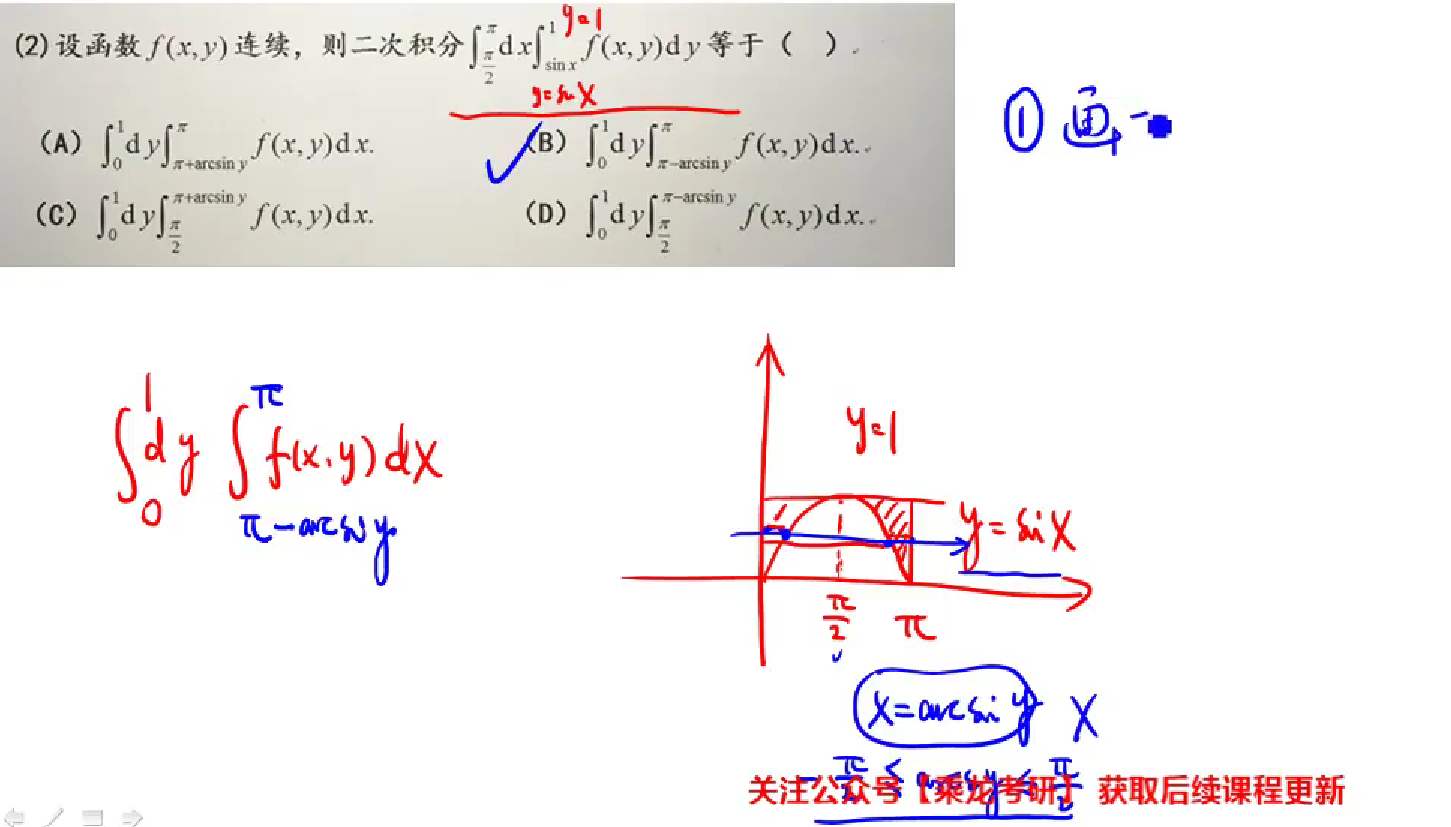
注意：arcsiny=x中x的范围是在(-π/2，π/2)，这里利用关于轴x=π/2的对称关系，转化

---

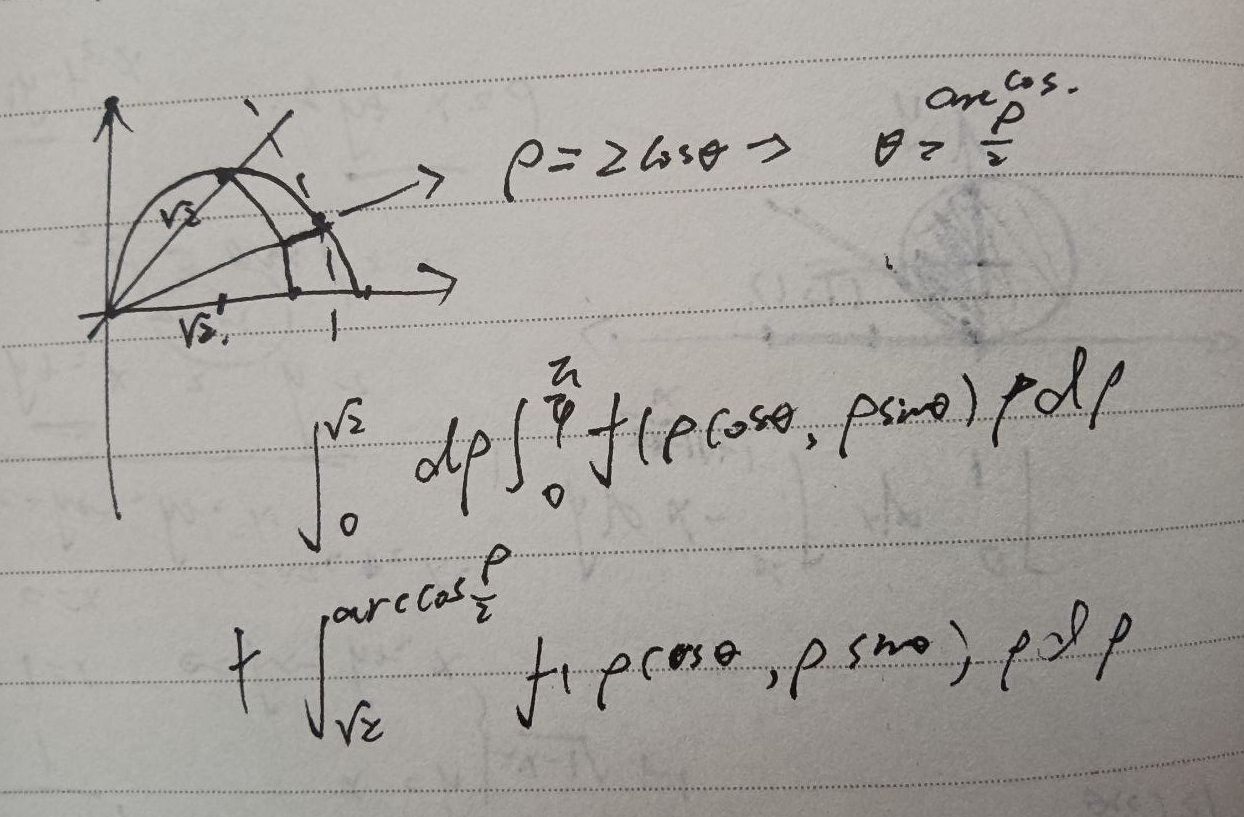
32

答案：

思路：运用洛必达去掉积分符号，但是，必须先将内层积分给积出来。但是，内层先对y积分明显积不出来，所以考虑交换积分次序。画出积分区域，先对x积分。

---

33🍊

思路：利用平移+奇偶性+极坐标

---

34

思路：化为二重积分

---

精选

1

答案👇

先拉格朗日中值定理+夹逼

2

答案👇

3

答案👇

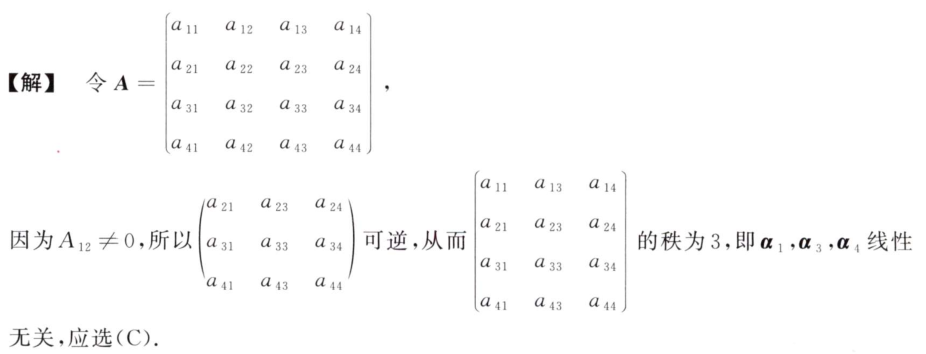
A.正交矩阵性质，向量互相正交，向量为e, 所以正交矩阵可逆。与B选项重叠
B.矩阵是否可以相似对角化的判断
C.非对称只能和非对称合同，实对称只能和实对称合同，如果一个矩阵不是对称的，那么不可能合同
D.是否与E合同，合同要满足正负惯性指数一致

4

答案👇

5

答案👇

6

答案👇

7

答案👇

8

答案👇

选择B
正交矩阵性质

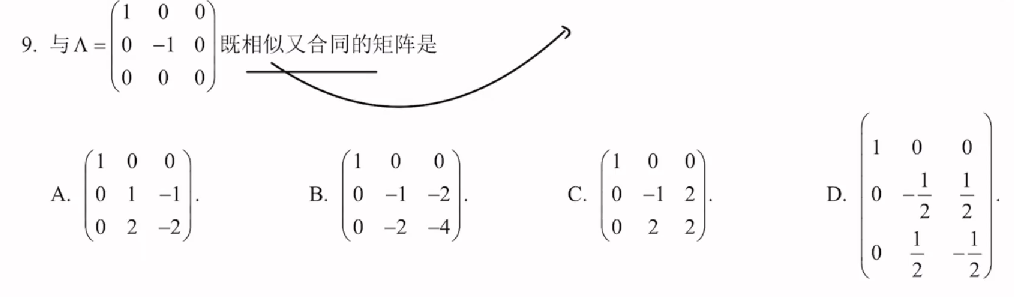
9

答案👇

10

答案👇

A.不是对角矩阵，所以不可能与对角矩阵合同，排除
B.对角线的迹，不同，排除
C.对角线的迹，不同，排除
D.只能选D

11

答案👇

求饶x轴面积，一定要注意当函数在x轴下方的时候。不能直接对区间求积分，需要取绝对值

12

历年真题

2023数二🎃

5

答案👇

8

答案👇

选择D

9

答案👇

拉格朗日配方法，必须每配一次将一个平方项配干净.

15

答案👇

20

答案👇

这一步一开始没想到

21

答案👇

微分中值定理题型，本题运用泰勒中值定理，进行泰勒展开。
第二问，运用放缩

2022数二🍊

7

答案👇

21

答案👇

法1

只需证明F(x)≤0恒成立，因为F(x)二阶可导，所以函数连续，即

故只需证明F’(x)≤0即可


因为x>a,所以f”(x)>0,才使得F‘(a)≤0。

法2
泰勒中值（高阶导、具体点、不等式）

20

答案👇

22

答案👇

正交变换不改变向量长度

• x^Tx是向量内积，也就是x向量长度的平方
• x=Py, P即是正交变换，只是换成以P为基底的坐标表示，实际y向量长度没变
  

2021数二🎁

7

答案👇

技巧：看x变量的变化跨度，与外面的可爱因子是否一致
A.变量x跨度是1/n,但是外层可爱因子是1/2n
B.变量x跨度是1/n,外层也是1/n符合
C.变量跨度是1/2n,外层是1/n
D.变量跨度是1/2n,外层是2/n

答案选B

8

15

答案👇

2020数二🍗

2

答案👇

注意：第二类间断点，可以是左右极限不一致，且至少有一个不存在。分别是2，1，-1

4

5

答案👇

反常积分审敛，根据lnx的性质，无论是趋向0+ 还是+∞，lnx趋向∞的速度都很缓慢

6

答案👇

构造辅助函数

7

答案👇

思路：A* A=|A|E . 因为|A|=0，所以A就是解的矩阵

18

20

答案👇

思路：柯西中值定理

21

答案👇

22

答案👇

拉格朗日配方法

• 拉格朗日配方法配出来的正交变换一定是可逆的
• 配成规范型, 由于合同特征值并不相等，但是正负惯性指数相同，所以利用规范型作为中间桥梁
  

23

答案👇

抽象矩阵相似问题
本题，第二问，实际考察对于将向量组合拆成矩阵相乘的能力

2019数二

14

答案👇

概念模糊：
代数余子式A，与余子式M，与行列式展开的关系没有理清
答案：-4

15

答案👇

做错的地方，在于忽略了不可导点，也可以是极值点。

16

答案👇

部分分式的拆解：

• 分母都可拆解为一次的因式
  
• 分母含有inrreducible的高次，其分子的式子比分母小一次
  
• 分母含有repeating项。
  

19

答案👇

利用区间再现，化繁为简

21🍗

答案👇

法2-多项式拟合

23

答案👇

2018数二🎉

1

答案👇

选B。考察泰勒展开

2

答案👇

注意：对于导数的定义要加深理解

4

答案👇

思路：函数f(x)在x=1/2处的泰勒展开，最后一项带有皮亚诺余项。

5

答案👇

⚠️upload failed, check dev console

8

答案👇

思路：考察秩的结论

17

答案👇

• 思路：由于无法画出积分域，所以只能设y=g(x)=1-cost，另外还要求很高的计算能力
• 最后积分运用表格法
  

18

答案👇

遇到这种项数多的式子

1. 先分析，缩小处理的部分，减小计算量
2. 例如这题，可以只对右因式处理，分为(0,1)和(1,∞)。

21

答案👇

单调有界

1. 证明有界：数学归纳法
2. 证明单调：拉格朗日中值定理

22

答案👇

23

答案👇

2016数二🍋

3

答案👇

要点：①中x->0^- ，②中x->0⁺

7

答案👇

19

答案👇

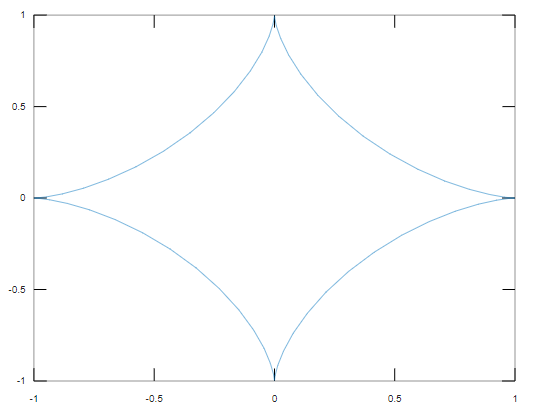
20

答案👇

参数方程为星型函数，图像如下：👇

*答案如下：👇*

23

答案👇

思路：

21

答案👇

2017数二🍇

8

答案👇

思路：👇
从特征值出发，三个的特征值均为 2, 2, 1.
要使得A与C矩阵相似👉A要能够对角化为C。
同理B也要能够对角化为C。
相同特征值必须有两个线性无关的特征向量，👉r(A-2E)=1
选择B

19

答案👇

第一问 略

22

答案👇

非齐次通解=齐次通解+一个特解(总是忘记加上齐次通解)

2015数二🥝

8

答案👇

思路：





选择A

21

答案👇

2014数二

17

答案👇

脑子糊涂了，一时间卡主了。

18

答案👇

info 提示塊標籤

20

答案👇

归纳法，找规律，推出第n项的式子

21

答案👇

22

答案👇

2013数二

10

答案👇

反函数的导数

19

答案👇

曲线的边界处x=0或y=0处也要考虑。边界处极有可能有最值

20

答案👇

23

答案👇

粗心de问题总结

1. 想当然，没注意题目给的条件，例如四阶矩阵，想当然认为三阶矩阵。
2. 最基本的加减失误，计算跳步，导致想当然的计算错误。
3. 求极限，指数化后，老是忘记指数e。
4. 求积分，计算时，总是忘记对数ln。
5. 打草稿，凌乱，导致列式子，前后总是丢式子,对于几次方写的自己都看不清。
6. 算曲率半径，总是求完曲率后还要求倒数。
7. 在一些很简单的地方卡壳,建议先跳过，回过头在看。
8. 利用泰勒展开求n阶导数时，最后总是忘记有n!
9. 选择题，总是看错选项，会做但选错。
10. 选填不会做，带特殊值。

张八

1

4

答案👇

选择D

6

答案👇

选D

8

答案👇

一个一个展开容易错，将某一行/列化0，简便计算

10

答案👇

广义初等变换

13

答案👇

平移坐标轴,注意是加还是减，答案二分之五π

19

答案👇

22

答案👇

• 实对称矩阵不同特征值对应的特征向量一定正交
• 实对称矩阵相同特征值对应的特征向量不一定正交
• 正交变换不改变向量的长度
  

2

9

答案👇

广义初等变换，左行右列

11

答案👇

info 提示塊標籤

20

答案👇

info 提示塊標籤

3

5

答案👇

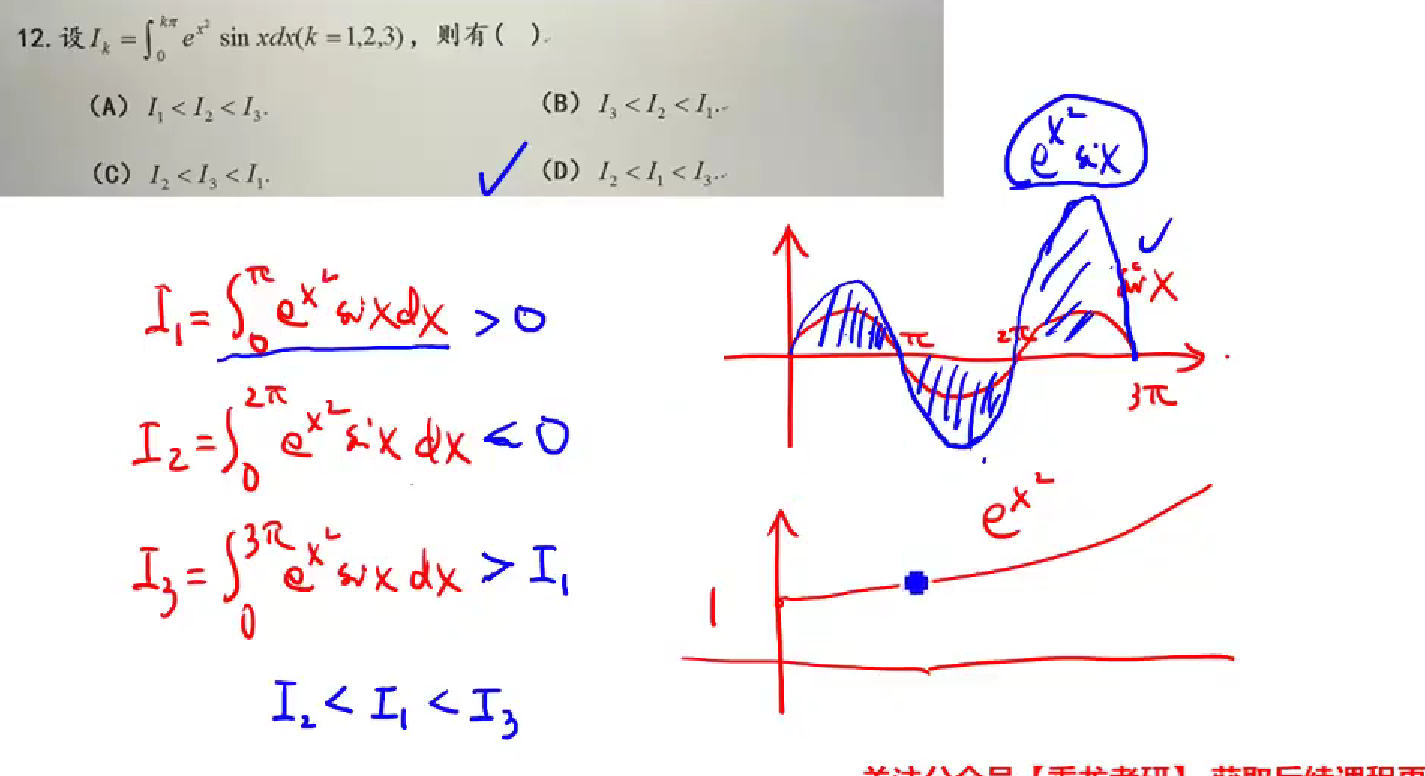
6

答案👇

• 画图法,根据起点相同，下降趋势不同判断。
• 对于I2，lnx增大速度比x的任意次幂都小
  

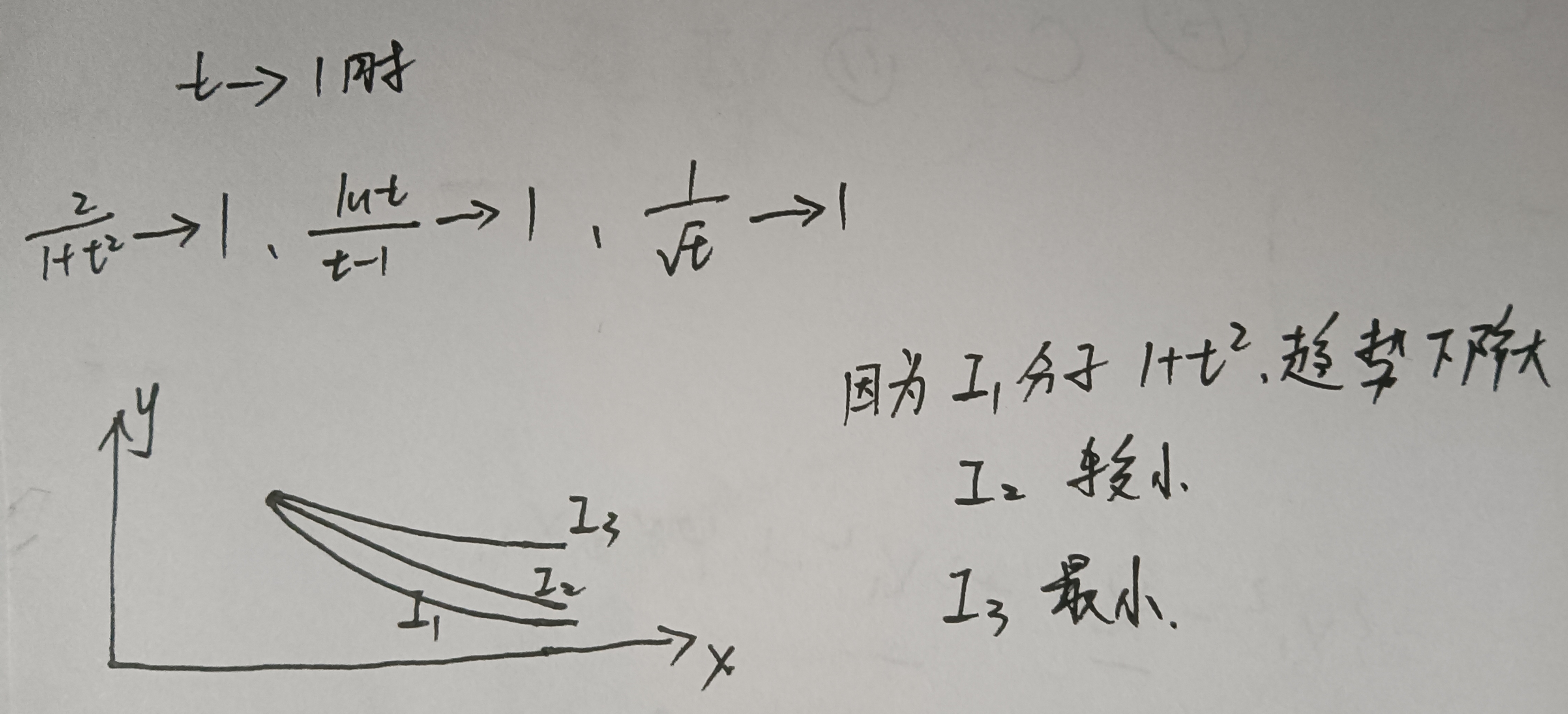
7

15

答案👇

21

答案👇

5

22

答案👇

张四

1

6

答案👇

矩阵多项式->十字相乘->提因式
=

21

答案👇

第二问求正交矩阵Q(正交且单位)，只能通过求特征值->求特征向量，求得矩阵P 再进行单位化正交化得到。因为不同特征值对应特征向量天然正交，并且单位化后任然是特征向量。配方法得到的变换矩阵没办法保证是正交矩阵和单位阵。

超越卷2023

1

4

答案👇

一维转二维积分

8

答案👇

这类比较向量组线性相关性的问题，统统转化为矩阵x矩阵的形式方便比较秩

9

答案👇

方程组同解

11

答案👇

以后看到求n阶导数，直接提出，剩下的直接代入，再乘以n!

21

答案👇

极坐标的换序积分

2

1

答案👇

4

答案👇

泰勒展开+带特殊值，非常的快速

5

答案👇

info 提示塊標籤

6

答案👇

判断函数可不可微

1. 先判断是否连续
2. 再判断是否可导
3. 最后凑微分看是否可微

8

答案👇

A的每行元素之和=Kk是A的一个特征值，(1,1,1)^T 是k对应的特征向量

推导链，所给的条件之间一定有某种逻辑联系，使用从后往前推导过程

10

答案👇

只有4是对的，选A

11

答案👇

使用区间再现

12

答案👇

注意跨度

20

22

3

6

答案👇

选B

8

11

答案👇

对称的区间，考虑区间再现

12

13

答案👇

必须考虑AC-B^2=0的情况

16

答案👇

17

答案👇

泰勒展开

22

答案👇

线代大题九大总结之一，运用谱分解定理

超越卷2024

1

6

答案👇

选择c

9

答案👇

10

答案👇

选择B。利用之前总结的结论

12

答案👇

方法1-任意项常数消去法

1. 两边连续求两次导数，凑微分方程
2. 得到三个方程，利用四则运算，将右边系数消去

方法2-变量替换，倒推

22

答案👇

3

4

答案👇

5

答案👇

8

答案👇

6

17

答案👇

微分算子法求特解

19

答案👇

info 提示塊標籤

7

5

答案👇

7

答案👇

15

答案👇

考察泰勒展开

凯哥微分中值总结

答案👇

预测

1

答案👇

2

3

答案👇

4

答案👇

差分方程法求三对角矩阵

5

答案👇

递推数列，首项不可知，xn-xn-1