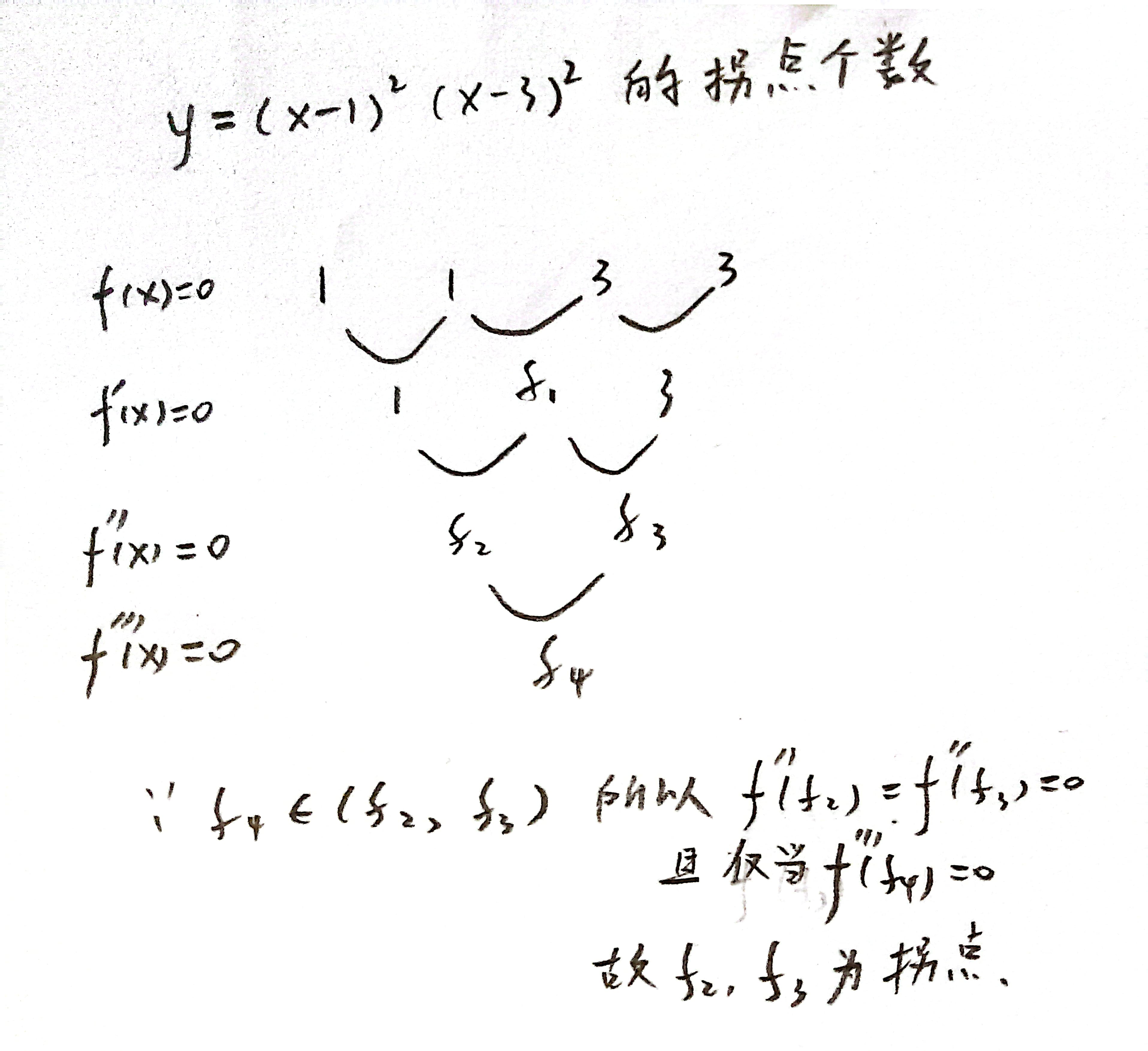
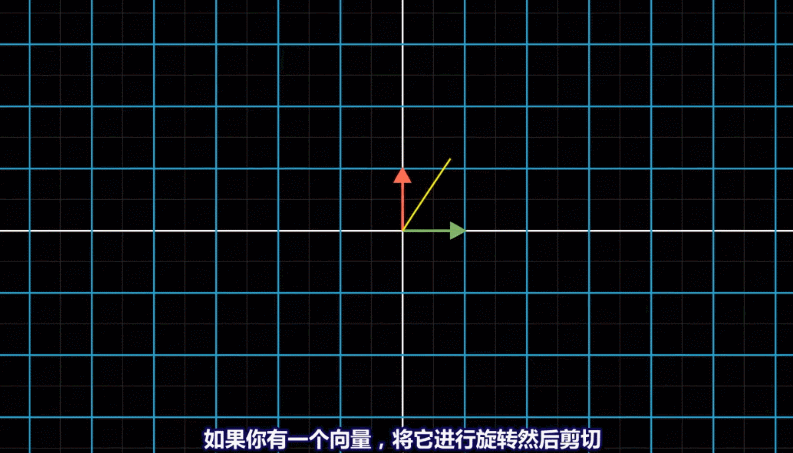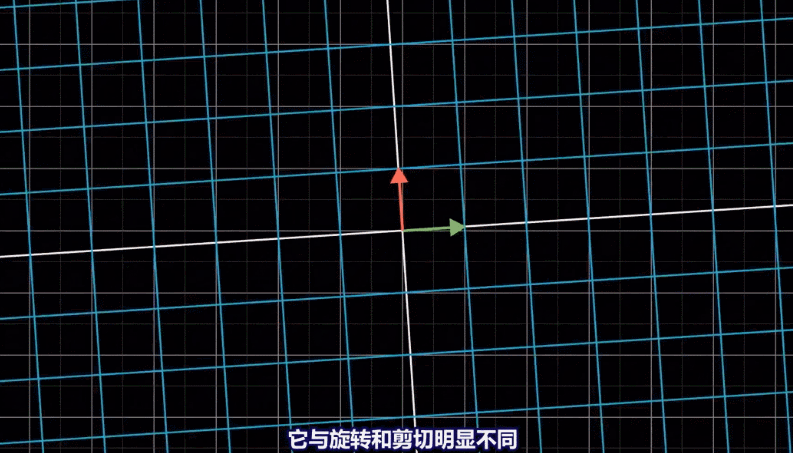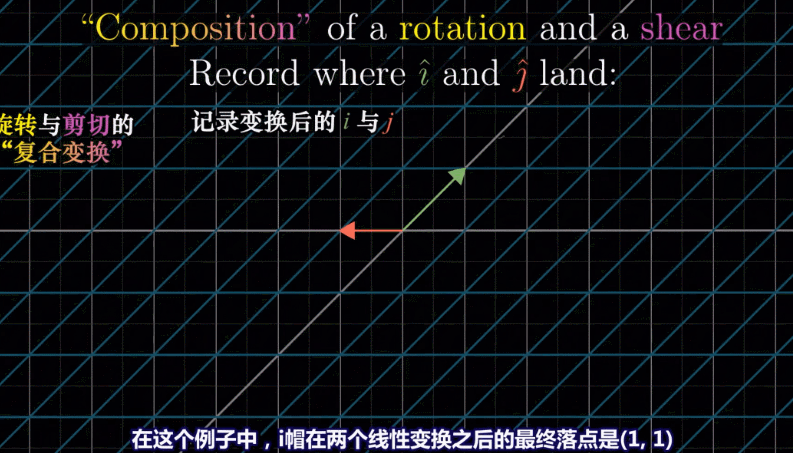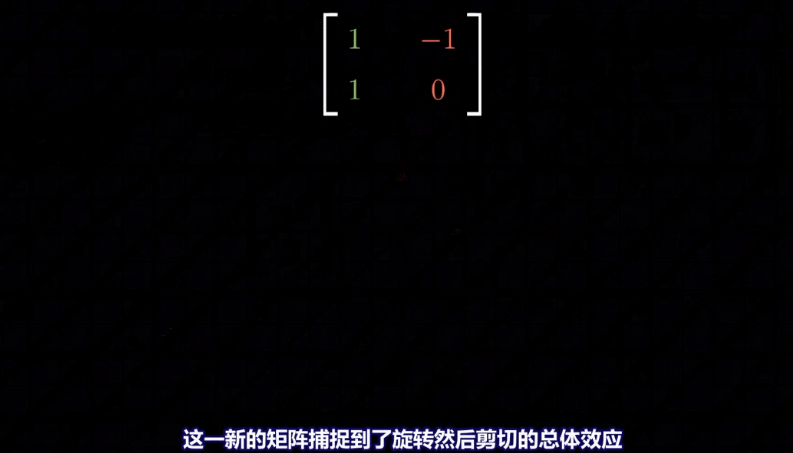
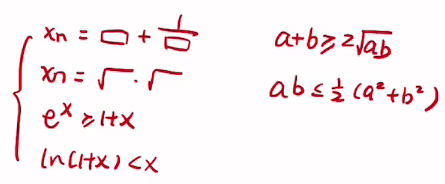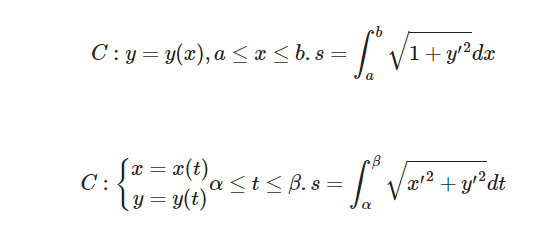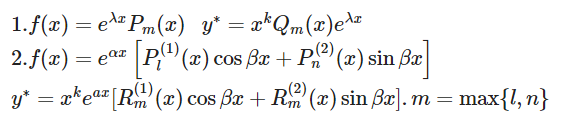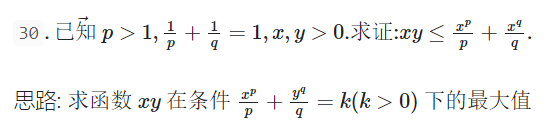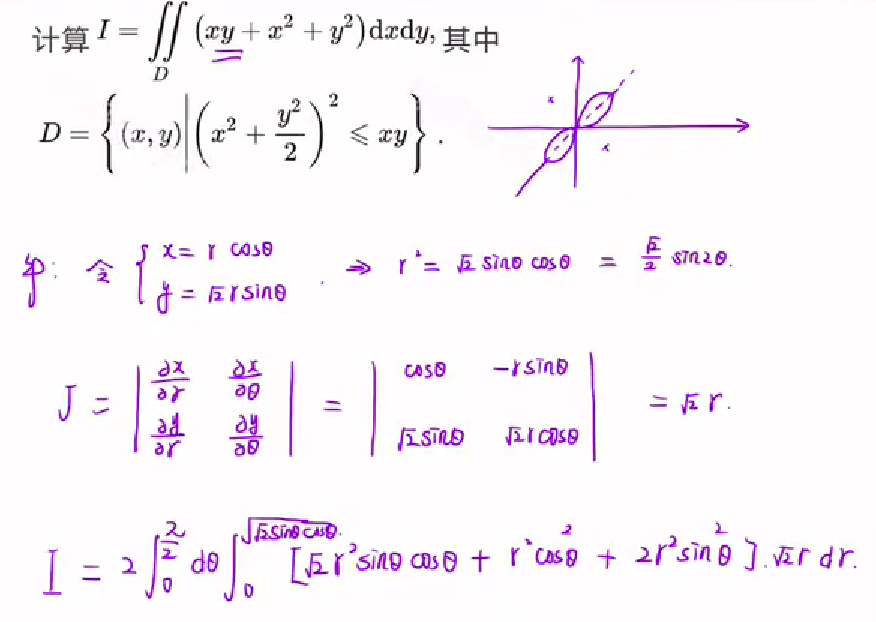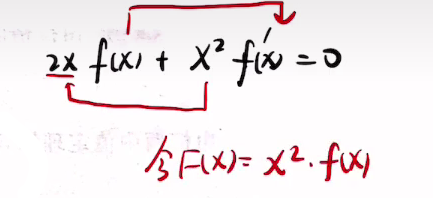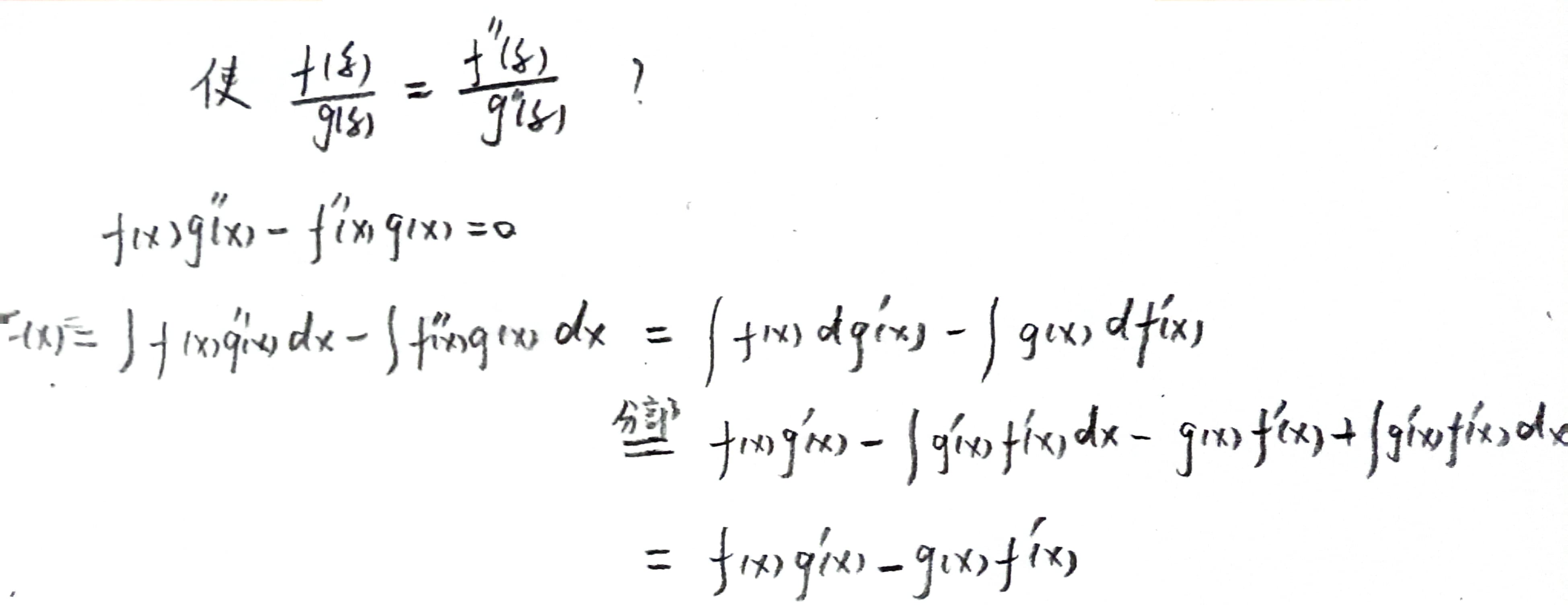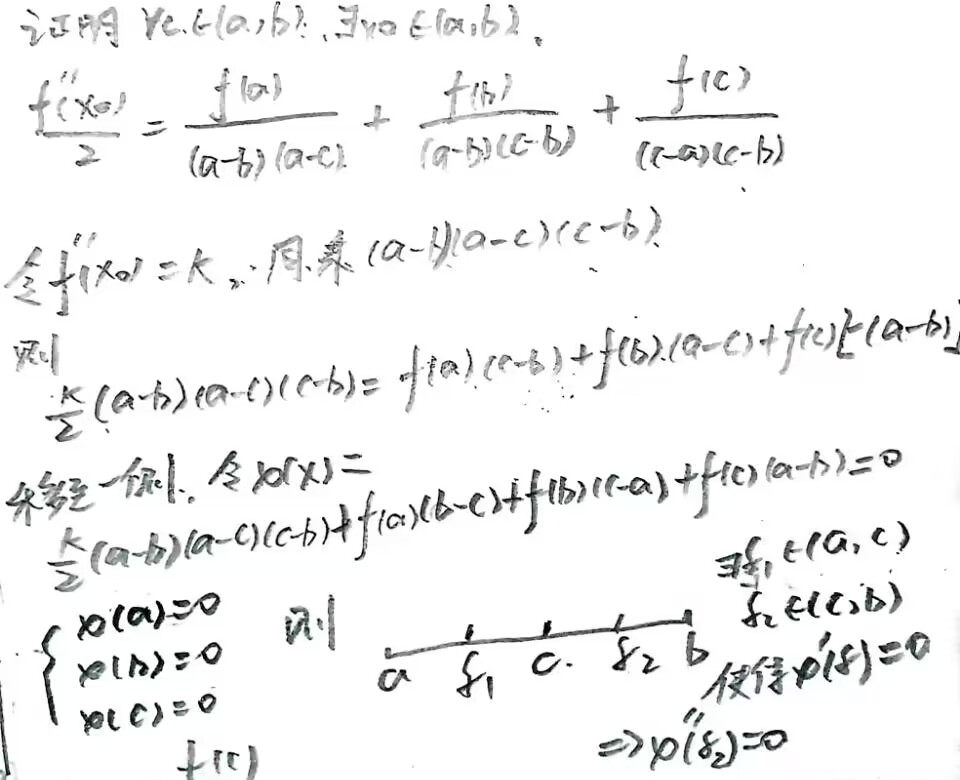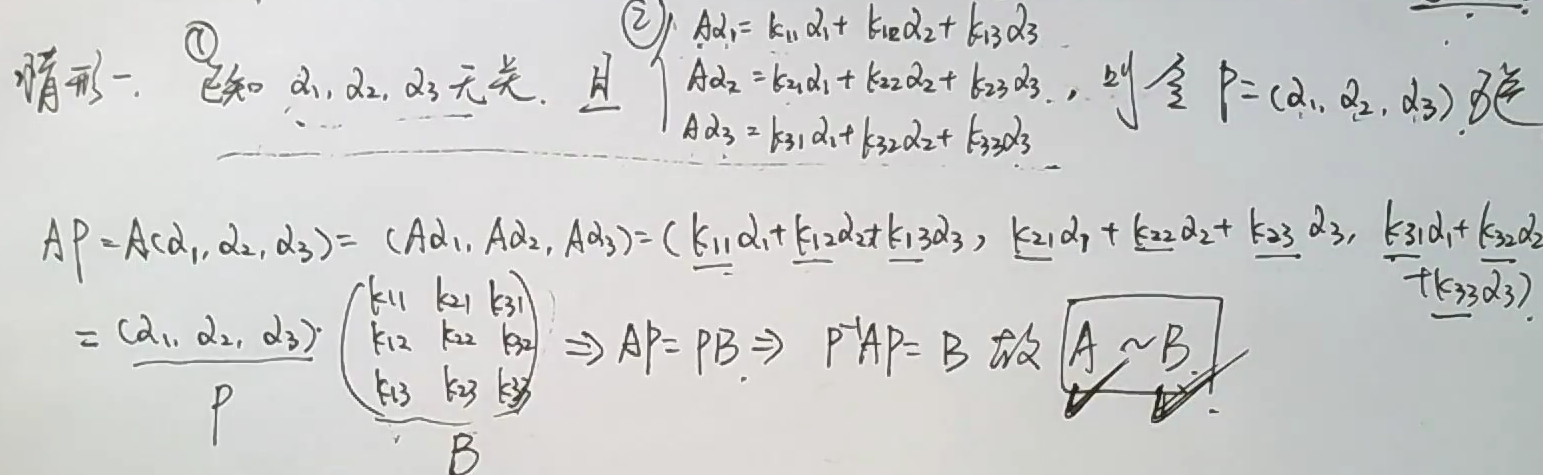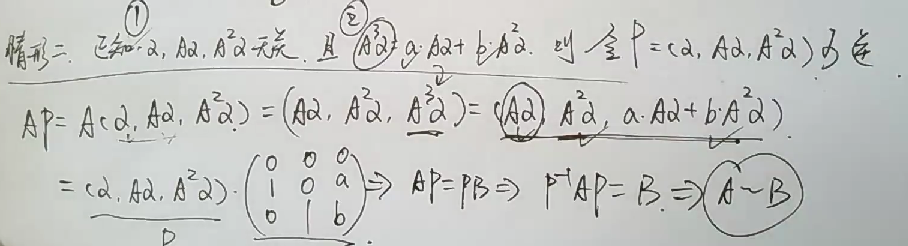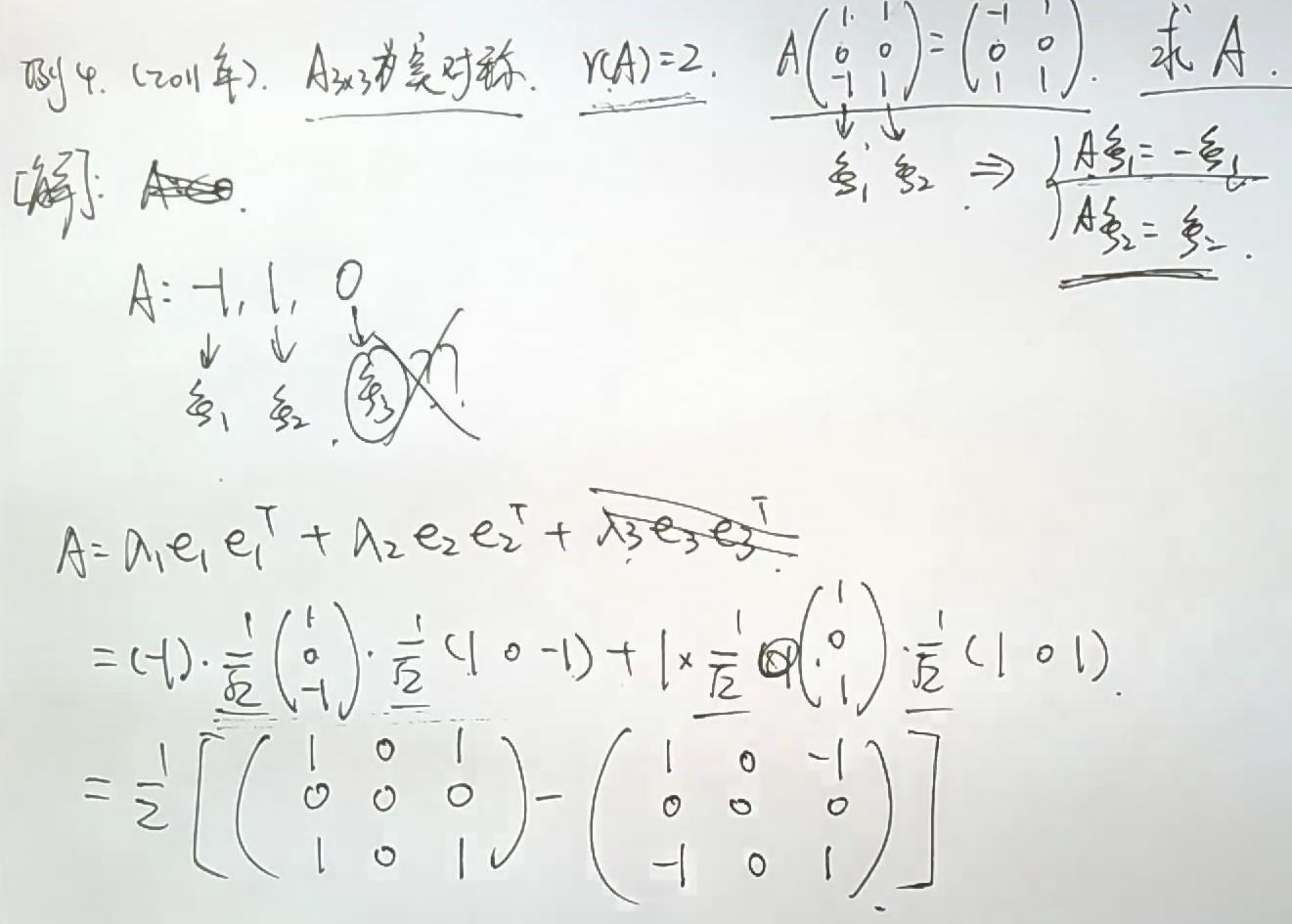formula
limt
函数极限
常用的无穷大比较
无穷大量与无界变量的关系
等价无穷小
a推广bc时 时 d
常用极限
不 存 在
型 若 且
则
泰勒公式
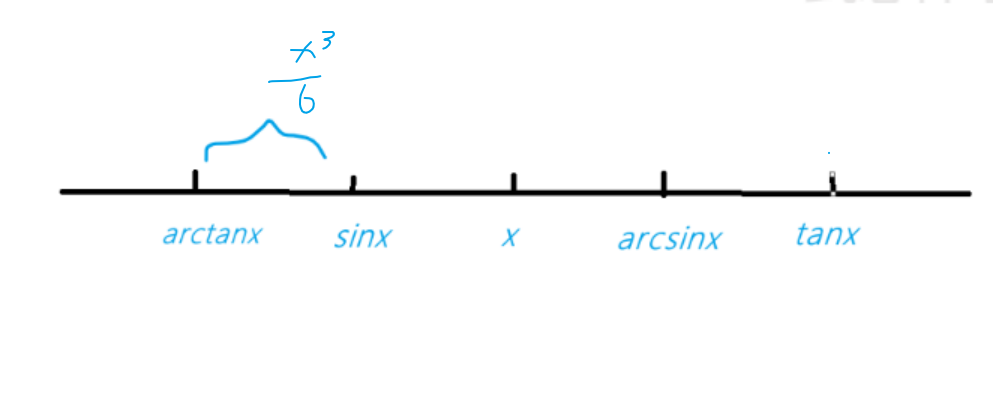
重要放缩不等式
求n项和的数列极限
当
变化部分与n次量级–用夹逼
当变化部分与n同量级–用定积分定义
平方项和公式
分母在变,分子也在变的–夹逼,然后定积分定义求 极 限
递推关系数列极限
证明数列收敛【数列收敛指的是第n项趋于一个极限】
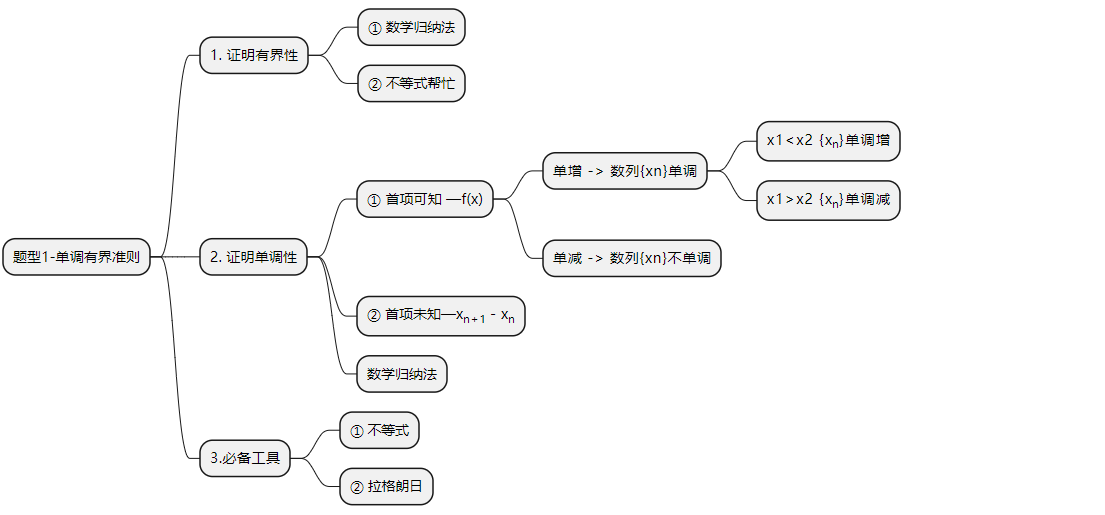
题型1.单调有界准则
题型2.压缩映射(先斩后奏)
①先假设数列的极限为A,想象趋向∞,求出A。
②验证A,列出式子 就能递推出 ,夹逼得出A即为极限
变积分上限无穷小量阶的比较
时, 是 的 m 阶无穷小 , 是 的 n 阶无穷小
则当时, 是 的 阶无穷小
continues
间断点的分类
1.第一类间断点:左,右极限均存在的间断点
2.第二类间断点:左,右极限中至少有一个不存在
Derivative
可导的概念:某一点x0处,左右导数都存在且相等
基本求导公式
高阶导数求导公式
1.求函数固定点的n阶导数,要么用求导公式,要么泰勒展开
2.求函数不定点的n阶导数【导数函数】,找规律或高阶求导公式
二级结论
设 其 在 处 连 续 在 处 可 导 的 充 要 条 件 是
Derivative applications
曲率公式
反函数的导数
方程根的存在性及个数
有 个 零 点 至 少 有 个 零 点 函数f(x)如果有n阶导数,n个零点,那么它至少n-1个驻点,至多n-1个驻点 至 少 有 个 零 点
Mean value theorem
构造辅助函数
欲 证 令
欲 证 令
欲 证 令
核心,记一个令
令
罗尔定理
拉格朗日中值定理
柯西中值定理
泰勒中值—拉格朗日余项! ! 介 于 与 之 间
1.单中值问题,一般只需要罗尔定理或柯西定理
2.双中值问题,要求两个中值不同,一般分为两个区间,然后两个区间分别用拉格朗日定理;没要求两个中值不同,分离两个变量到两边,用拉个朗日或柯西
3.单中值,高阶导数问题,一般泰勒展开,在提供信息最多的点展开
中值证明题两种思路
1. 构造辅助函数
2. 涉及高阶导数,尝试泰勒展开。或者区间分两块,用两次拉格朗日,得到二阶导数
Definite integral
本质是由区间再现公式推导得出
点火公式
为 正 偶 数 时 为 正 奇 数 时
重要积分不等式
线
质心
形心面
质心
形心
indefinite integral
原函数存在
原函数必须是处处可导的函数 => 有第一类间断点的函数一定没有原函数
不定积分基本公式
积不出积分
三角有理式积分
(1)一 般 方 法 万 能 代 换 令
(2)特 殊 方 法 三 角 变 形 换 元 分 部 若 则 令 若 则 令 若 则 令
Improper integral
无穷区间审敛–比较法极限形式
则 当 时 与 同 敛 散 当 时 收 敛 收 敛 当 时 发 散 发 散
一般与P积分比较
无穷区间的反常积分
收 敛 发 散
无界函数的反常积分収 敛 发 散
Applications of definite integrals
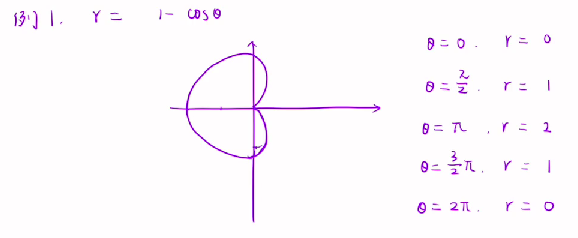
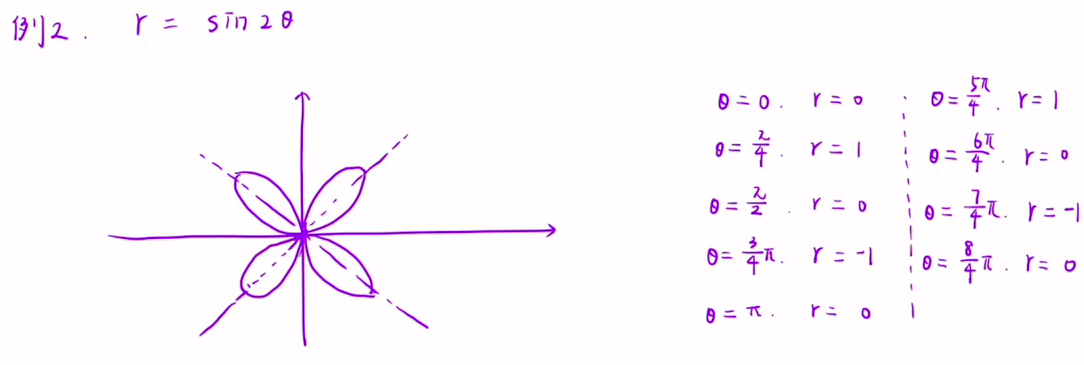
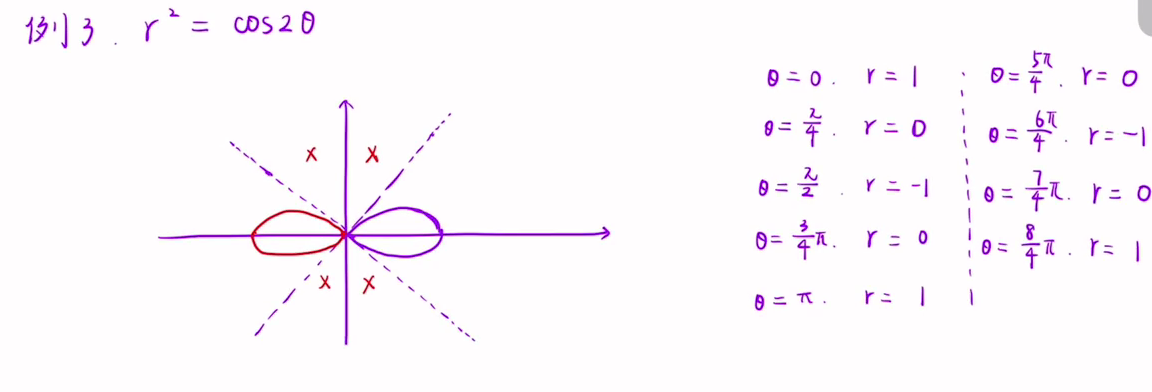
极坐标平面图形面积
若 平 面 域 由 曲 线 所 围 成 , 则
绕x轴转旋转体体积
绕y轴转旋转体体积
曲线弧长
旋转体侧面积
differential equations
线性方程公式通解
可降阶微分方程代换方式
1.包含有x的,令y’=p,p作为x的函数
2.只含有y的,令y’=p,p作为y的函数
高阶常系数线性微分方程通解公式
不 等 实 根 相 等 实 根 共 轭 复 根
高阶非齐次线性微分方程特解公式
常用积分
奇怪的微分方程利用xy对调
解微分方程求y表达式
解得
时,立马写出其共轭式
相加消去,即可求出y(x)表达式
Differential calculus of multivariate functions
定义法判定可微性
与 是 否 都 存 在 是 否 为 零
题目给
类微分定义式时,求全微分dz
方法1. 凑微分定义式
方法2. 直接找分子式中 , x 和 y前的系数乘-1就直接是两个偏导数
题型1-多元分段函数函数判断是否连续、偏导数存在、可微
- 判断是否连续:a.化极坐标,求该点极限 b.对函数加
绝对值->放缩(不等式)->夹逼,判断极限是否存在- 判断偏导数是否存在:利用偏导数定义式
- 判断是否可微:凑可微判定式,前提需要求出两个偏导数
题型2-给了含多元函数的极限等式,判断多元函数是否连续、偏导数存在、可微
- 判断是否连续:能拆则拆,将分式化简,例如(将极限=0的分式,消去),然后求极限
- 判断偏导数是否存在:利用定义式
- 判断是否可微:凑可微判定式,
没有偏导项->设偏导均为0,于是就是一个可微判断式
f(x,y)是n次齐次函数时
则 有
微分形式不变性
无约束极值–判断是极大值还是极小值点
记 则
当 时 有 极 值 极 小 值 极 大 值
当 时 无 极 值 当 时 不 一 定 化 二 元 为 一 元 取
条件极值–拉格朗日数乘法
函 数 在 条 件 条 件 下 的 极 值 令 快速解法: 由于太碍事,所以消去,简便运算
获得x与y的关系,代入第三个式子
任选两组,组成上例的形式,解方程
条件最值总结
求条件最最值的问题,一定是一个区域D外加边界。首先没有边界限制情况下求驻点P。若驻点P在区域D内部且只有一个,那么必定是该条件最值(最大或最小);若驻点P 在区域D外部,则最值D内没有极值点,最大最小值在边界上(此时使用拉格朗日数乘法)。
条件极值证明不等式
利用其中一边作为约束条件,构建拉格朗日数乘法,求左边的极大值,并且计算其最大值不会超过右边, 如下举例
保号性判定抽象多元函数极值
例求f(x,y)在(0,0)点是否是极值点?极大还是极小?
答:左式整体取负,分母=>0+ , 所以分子=>0- ,所以邻域内f(x,y)<f(0,0),所以(0,0)极大
double integral
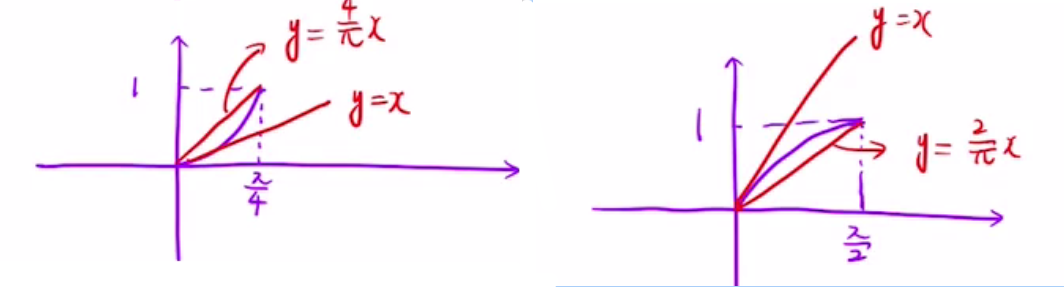
二重积分之直角坐标转换成极坐标画图
- 画图对于单
- 画图对于2
- 极坐标没有负数,当求出r<0时,其实是,按照当前所在角度,其原点对称位置画r轨迹
有时候不能简单的令x=ρcosθ,y=ρsinθ 不好计算
- 直角坐标换成极坐标本质就是换元
- 引入变换
乘以雅克比行列式绝对值 - 其中雅克比行列式
二重积分计算方法
- 交换积分次序
- 转换极坐标(极坐标不好积时,有时还需要
极坐标换序积分)- 利用奇偶性
- 变量对称性
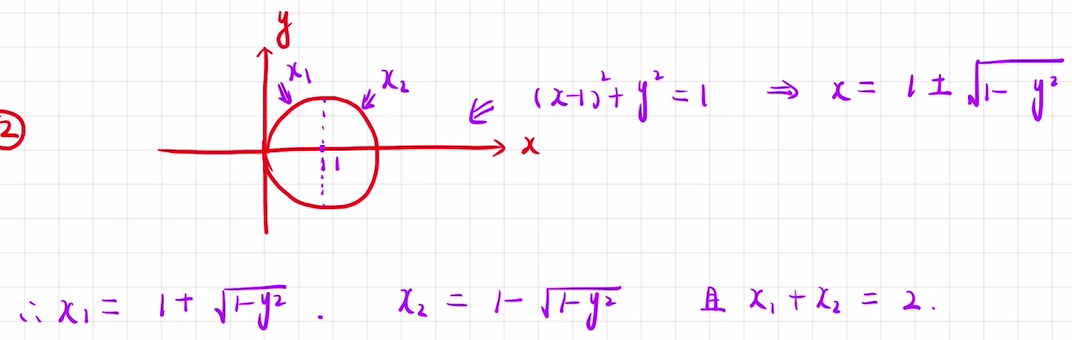
- 平移积分区域+椭圆变圆
- (椭圆方程
令u= v= 转化为 ,计算) 看到规则图形,首先尽量利用奇偶性和对称性(平移,凑奇偶性),极大简便运算
变量对称性
1.变量对称性 关于y=x对称
2. 扩展变量对称性, 关于y=-x对称
反解求图形的对称轴
有的函数式子,无法转化为极坐标画积分区域,需要有一种方法,判断该图形是否关于某个轴对称,反解求x=a的对称轴, 正解求y=b的对称轴
变上限累二重积分的极限问题
三个步骤
1.交换次序
2.洛必达
将内层的积分看做函数g(u)
3.积分中值定理
二重积分积分次序可换
skills
定积分比大小问题-相同区间
- 对称区间,可利用
奇偶性,比较被积函数大小- 可以
画图像解决,一般是被积函数起点相同,比较变化速率- 被积函数 和具体的数比较例如
1- 利用
不等式,;x+1 ; lnx ; ln(x+1) 之间的比较 - 有关三角函数定积分比大小的一些结论
6. 不好比较的尝试用用泰勒展开
反常积分审敛
- 找等价无穷小
- 比较各类函数趋近于0的快慢,一般与
作比较 - 比较各类函数趋近于无穷的快慢,一般
- 对
lnx的几种情况!比 都 慢 等 价 于 比 都 慢
递推数列证明题求极限,求如何证明单调有界
- 递推式出现相类似函数,例如
、 ; ; 考虑拉格朗日判断单调性 - 具体问题具体分析
中值定理辅助函数的构造-用罗尔定理
- 肉眼观察
- 求解微分方程
比如求的辅助函数,解微分方程得 即
解出的c即为辅助函数F(x)。因为F’(x)=0公式法(前面有总结):令 - 乘积求导形式
,构造原函数, 划线法,找出发点- 交叉式,高阶(二阶)导相乘形式
,构造原函数, 积分法- 一次积分构造得到的原函数与题目所给条件无关联,可以考虑做两次积分,再求一次原函数
- 能用拉格朗日解决的中值问题,一定能用构造辅助函数再用罗尔定理解决
- 能够用柯西解决的中值问题,一定能用构造辅助函数在用罗尔解决
多中值-互不相同-用拉格朗日 或柯西
多中值几种类型
- 两个不同中值,假设一个c1划分区间,
由(a,c1)和(c1,b)用中值定理获得 - 两个不同中值,假设一个c1划分区间,c1本身也是一个中值,
位于其中一段区间 - 三个不同中值,假设c1,c2分别划分,三个中值分别在各自区间用中值定理获得
- 三个不同中值,用一个c1划分,同时c1本身也是中值
泰勒中值证明
什么时候用泰勒中值?——当题目条件出现,高阶导数,和f(a),f(b)这些具体点时候;且出现这些特征时 题型1
- 一般在两个端点展开a,b,或者中点展开
- 常常结合带有绝对值的不等式证明,想到
用来放缩
题型2
- 题目中所给函数
n阶导数连续,但是给你的泰勒展开式只展开到n-1阶,没展干净- 此时就,自己展开到n阶,然后两式对比,相加减,获得里面的信息
多项式拟合-微分方程证明
- 适用情况 证明
(k为常数) - 可构造
(g(x)为多项式,具体次数看 是几阶导数) - 这样构造目的是为了g(x)求导保留常数
- 根据题目条件保证f(x1)=g(x2), f(x2)=g(x2)… 求出g(x)的多项式系数
- 得到F(x1)=F(x2)=…=0 ,即多次罗尔定理,可得到一中值,使得
,等式成立 就是所求常数k
常数k值法-微分方程证明
适用条件
- 适用情况 等式一端仅是与区间端点 a,b及其函数值、导数值有关的常数;另一端是只含导数函数 和函数在区间内某点(中值点)的值,即
- 如果把式中b换作a时,原式呈0=0形式,则称它是对称式
使用步骤
例👇
积分不等式证明通法——构造变限积分
若条件出现,可令
- 天然可得到两个信息F(a)=0,F(b)=A
- 接着凑微分、分部积分
例👇
多项式零点、极值点、拐点个数
- 极值点——f’(x)=0
- 拐点——f’’(x)=0,f’’’(x)
0 - 先将所有根(包括重根)列出来,再罗尔取中间必有1个下一阶导数为0的点(重根之间任然取回原来的数)
告别施密特正交化
- 实对称矩阵
不同特征值对应的特征向量一定正交- 实对称矩阵
相同特征值对应的特征向量不一定正交,所以需要正交化- 一个特征值的多特征向量,其实可以写成通解,然后随意选取一个向量,再选取另外一个,与之正交即可
AB=O大总结
- B的列向量,均为
A有特征值0,A有特征向量(B的非零列向量)A列相关—A列不满秩(因为Ax=0有非零解)B行相关—AB=0
相似大总结A∽B
- 秩、迹、行列式相同
- 对于任意a, 有
A-aE∽B-aE - $A^T\sim B^T,A^{-1}\sim B^{-1}, A^{}\sim B^{}$
线代大题九大考法
- 逆用矩阵乘法,结合相似理论
点击👇
- 已知特征值、特征向量,反求矩阵A(尤其是实对称 )
普分解定理点击👇
- 求逆矩阵P s.t
点击👇
info 提示塊標籤
同时相似对角化 s.t A. B 求P 使得
证明A、B共用一套特征向量点击👇
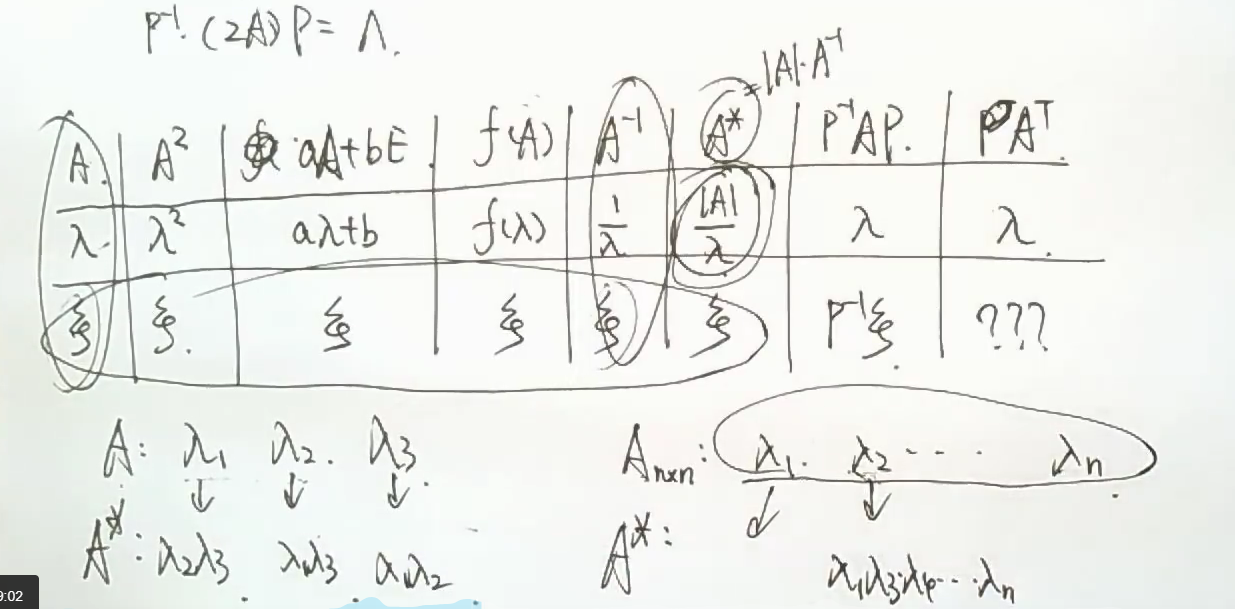
伴随矩阵A的特征值
要证明AB=BA,两个矩阵可交换,思路是证明f(A)g(B)=g(B)f(A),把括号打开,得到AB=BA
对A的各种变化不会改变特征向量
利用相似对角化 求
线性方程组与特征值特征向量结合
点击👇
求f(x1,x2,x3)=0 的解
将正定矩阵A ,分解为
答案👇
非对称矩阵的二次型问题,
区间再现求积分
- 对称区间的积分一般想到的是奇偶性
- 对称区间也很好使用区间再现
注:区间再现公式是普遍适用的常见需要运用区间再现解决的类型:
其 中
逻辑链推导法
很难形成思路,是因为没有在乎各个条件之间的逻辑关系,通过逻辑链一步一步推导,就能渐渐找到思路
微分算子法求特解
表示对f(x)积分 表示对f(x)求导
型1
型2换 ,D项用平方差变成平方项,重复 换 ,直到消去D
型3的 多 项 式
型4x的多项式
注意: 公比q只含D,这样才能使得P(x)求导为0
隐函数求驻点处高阶导技巧
- 一元函数
(通用) , (仅驻点处) - 多元函数
(三个都仅驻点处)
伽马函数例:
有理函数分式拆分技巧
型1
答案👇
型2
答案👇
计算心得
求导-> - 立方差公式
- 有理分式化为等比数列n项和形式->求n阶导数
是奇函数 - 椭圆面积=