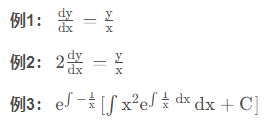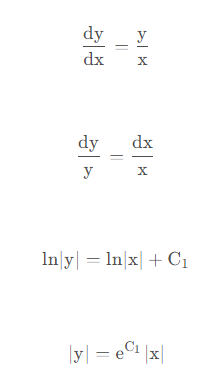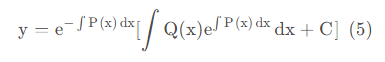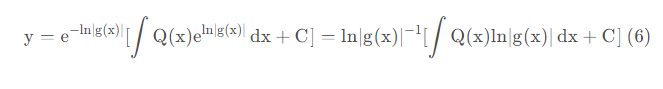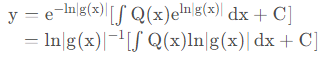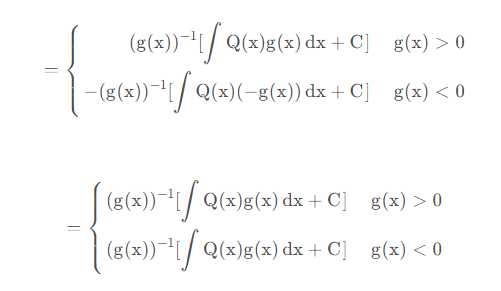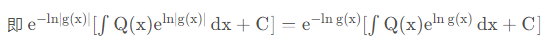关于一阶线性微分方程绝对值问题

摘要

在做某些微分方程问题时，有些题目的标准答案要加上绝对值，有些又不用加。按理说凡是涉及 ln 的我全加上就好了，但是加上绝对值又不便下一步计算，为此特地查阅一些资料，将考研数学微分方程中绝对值相关问题整理记录。

问题提出

开头提到的微分方程中绝对值问题其实本质上就是不定积分中对 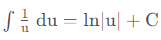中绝对值的去留问题。

分析与讨论

对于例1很好分析，我们按照常规方式来求解。

此时由于 y= ±e^C₁|x|，而如果我们令 ±e^C₁ =C₂，此时上式可以写为 y=C₂x，也就是说绝对值可以去掉，且C₂≠0。
但是上述讨论不具有一般性，不够严谨，我们还可以通过判断函数族是否相同的方式来判断两个解函数是否为相等。
那么现在问题描述如下：

如此一来对于经过积分运算，得到形如 (1) 式的微分方程的通解，是否去掉绝对值，取决于我们的选择，若去掉绝对值（即表示为 (2) 式的形式）则需要先将对数函数变为指数函数，再更改C₂的范围由任意常数到非零常数。

对于例2，求得的通解形式为 ln|y|² = ln|x| + C ,此时取对数y² = e^C|x|，显然绝对值是无法直接去掉的

但是对于例3却并不能用上述结论，因为一阶线性微分方程的解

的函数族不同于 (1) 式确定的函数族。那么当我们遇到 这种情况，绝对值是否可以省？

下面经过分类讨论来证明 (6) 式中 e 右上角的对数函数内的绝对值符号可以省去，不影响一阶线性微分方程的解。

所以例3中的绝对值可以去掉。

结论

对形如 l n ∣ g ( x , y ) ∣ = φ ( x , y ) + C 的微分方程，可以通过变对数为指数，同时改变常数​C₂的取值范围来去掉绝对值。对一阶线性微分方程通解同时，可以对 e 的右上角的指数同时去绝对值。