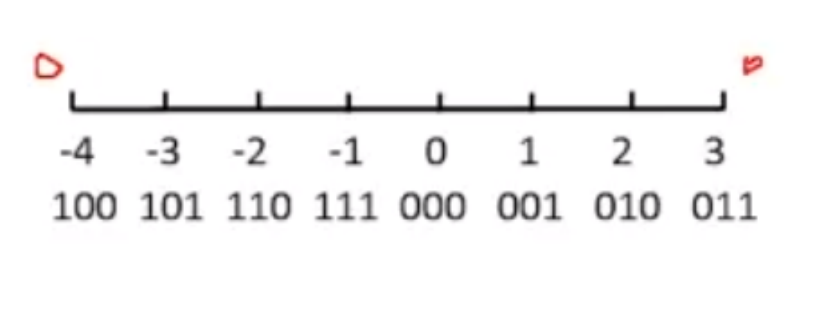
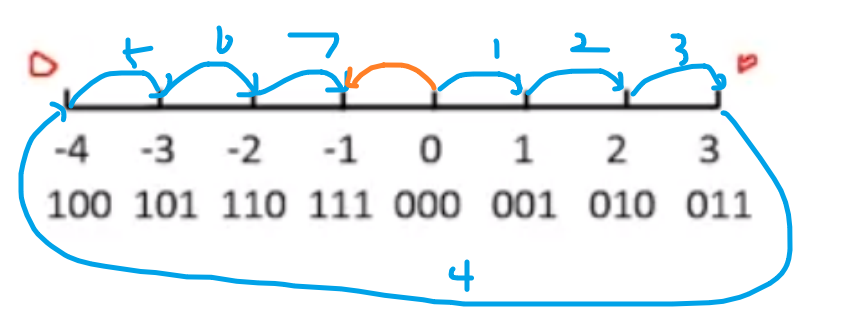
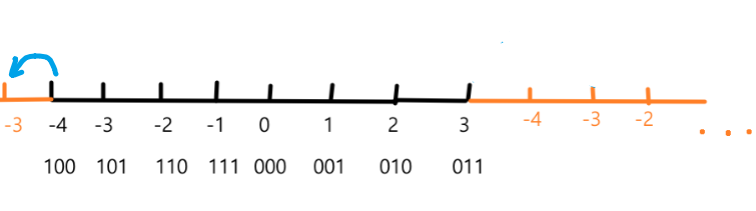
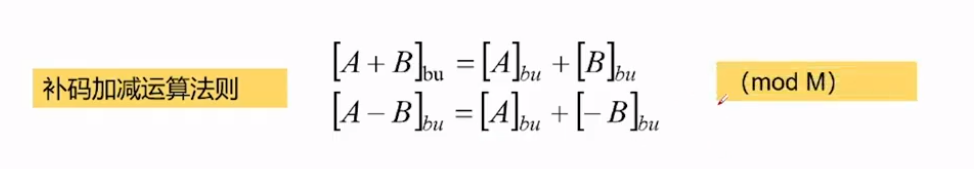补码、模与运算
引入补码的原因
1.原码的符号位无法参与运算
1 | //例如原码 3位数值位,1为符号位 |
2.将减法变加法
1 | //只有负数才有补码 |
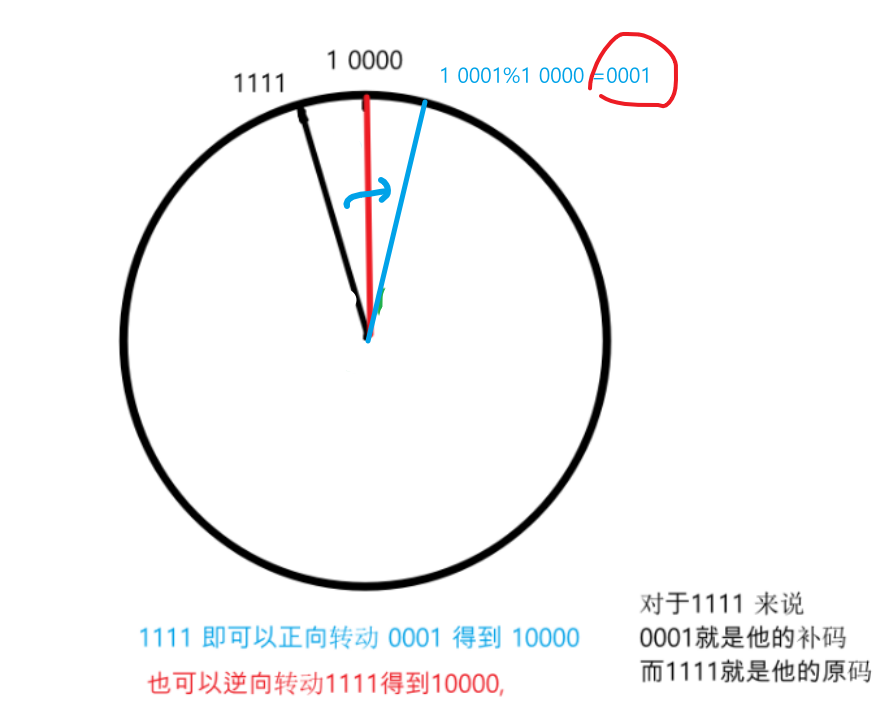
补码的“补”的含义
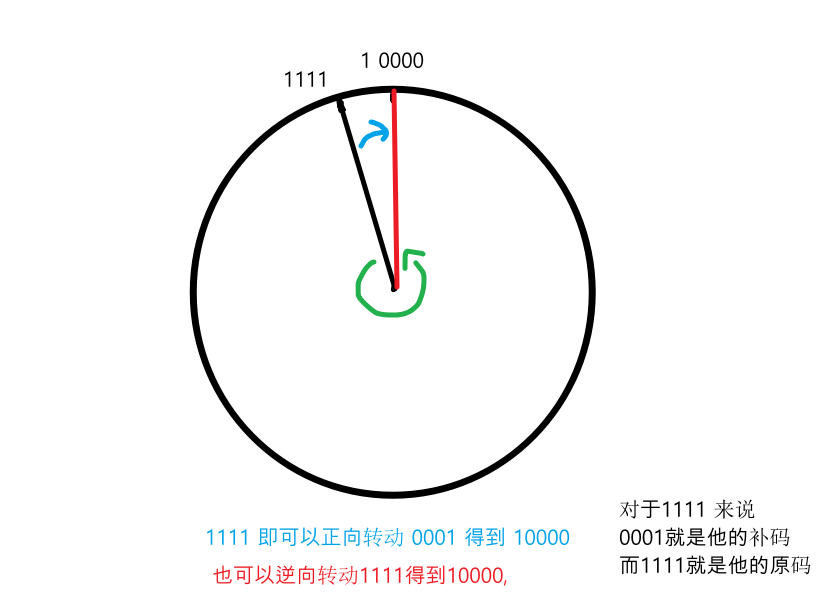
其中模M=10000,所以对于1111来说他的补码就是10000 - 1111 =0001;
补码加减运算
补码相加相减应该并不陌生。但是由于bit限制,存储的位数不够,补码相加或相减得到的数字超过最大或最小值时,就会发生符号位进位–>也就是溢出。
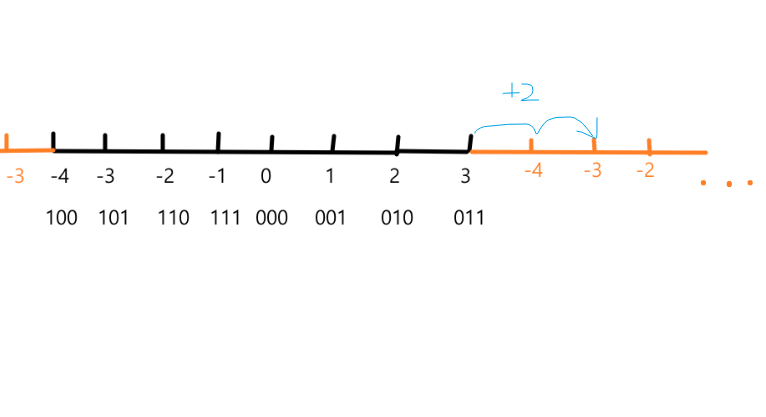
这个时候就需要通过取模运算,即有点像循环数组,超过最大模,则回到开始位置
所以要想补码计算正确,前提是,两数相加或相减不能超过模的绝对值,不然取模就不准确。
补码取模
- 定点小数
- 定点整数
补码取模,对于这个具体模的选取,有下面这样的规律。
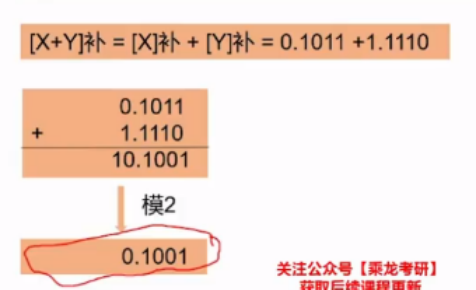
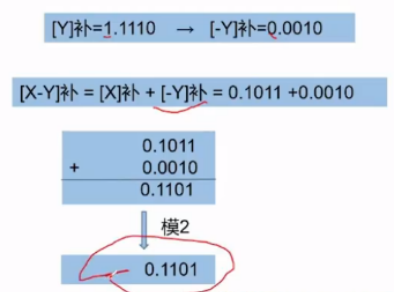
当参加运算的数是定点小数时,模M=2
当参加运算的数是定点整数时
模M=2^(n+1),n+1表示n位数值位,1位符号位;n+1代表总共存储位
1 | [x]补 = 1100 0000 |
1 | [x]补 = 100 --> -4 |
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 风起之时'blog!