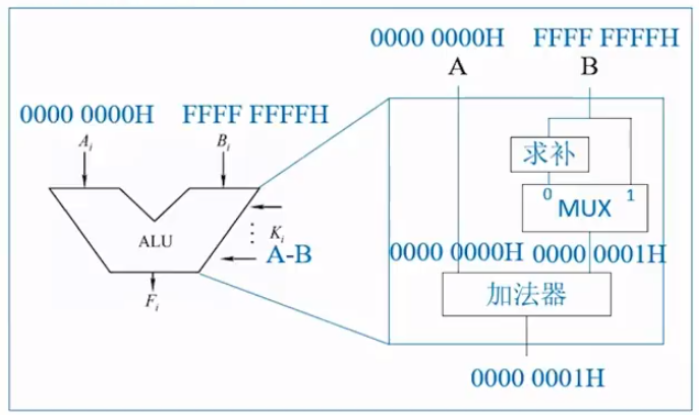
机器数内部运算逻辑
- 机器数一般都是补码,是由于补码可以对于有符号数进行机器运算。
- 本质上,机器处理二进制串只是做简单的与运算,不会在乎是不是补码。
- 我们所说的补码的运算规则是由于经过了ALU的一系列操作后,而反应的一种规则。
- 所以我们在做机器数的运算时,不需要管那么多运算规则(背后已经被ALU转化过了)
补码的移位
对补码左移运算
书里介绍的是补码左移符号位不变,仅仅数值位左移,低位补0.其实这是不准确的说法。这是建立在补码左移数值不溢出的情况。以8bit存举例。
1 | 1111 1110 补码 -2 |
但是如果负数补码左移,发生了数值溢出,也就是。
1 | 1011 1111 补码 -65 |
以另一种方式左移,也就是将符号位一起参与左移。
1 | 1011 1111 补码 -65 |
因此,实际上机器上处理补码的左移,只是对二进制串进行简单左移。
只是在补码没有溢出的情况下,数值最高位会始终为1,左移补上符号位后,表面上看起来符号位没有发生变化,实际上符号位向高位左移了。
所以补码左移连同符号位一起左移,不溢出的情况正负性不改变,溢出的话正负性变化
补码右移
- 正数补码:高位补0,低位舍去
- 负数补码:高位补1,低位舍去
1 | 两者本质上都是符号位参与了移位,只是,右移只会使数值减小,不会发生溢出 |
1 | 1011 1111 |
ALU对于运算规则的底层实现
①ALU的加减运算:[A+B]补=[A]补+[B]补[A-B]养=[A]补+[-B]补
A 、B对应的补码分别为0000 0000H , FFFF FFFFH。两数进行运算时,分别从ALU两端输入。
A add B时,A B的补码分别做机器相与运算A sub B时,B取相反数,对于补码来说就是全部取反(包括符号位),后再加1。然后再对A的补码与[-B]的补码做与运算
CF标志位如何判断?
- CF标志位,进位/借位标志位,针对于
机器数是否溢出的标志 - CF=最高位进位 ⊕ sub
- sub (减1,加0)
1 | 补码相减 0: 0000 [减去] -1: 1111 |
OF标志位如何判断?
- OF标志位,有符号数溢出标志位,针对于有符号数是否溢出的标志
- OF=最高位进位 ⊕ 次高位的进位
1 | 补码相减 0: 0000 [减去] -1: 1111 |
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 风起之时'blog!