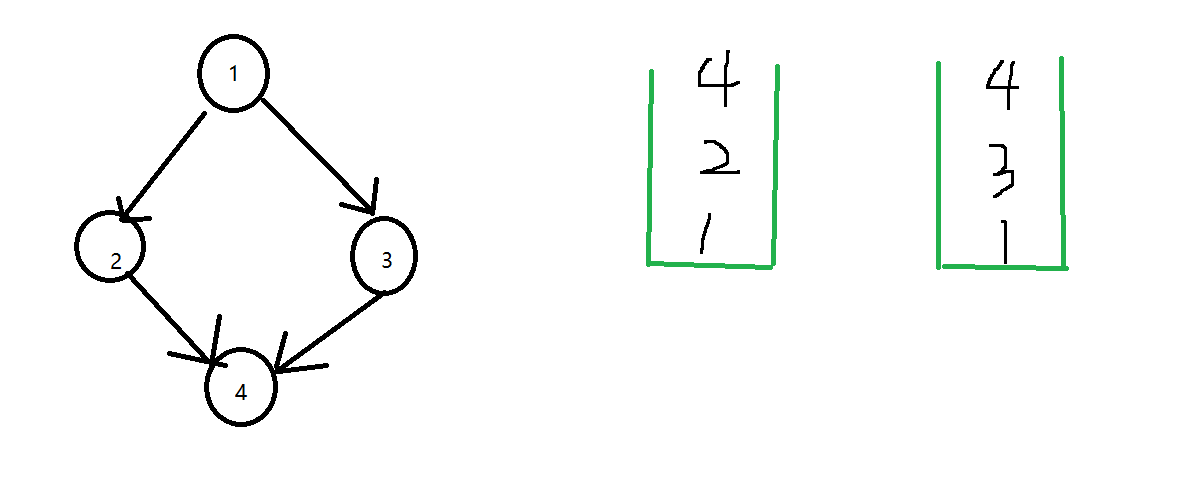判断有向图是否有环
关键路径
关键路径能否判断有向图是否有环存在争议
关键路径有争议,因为求关键路径,需要先求各个事件的最早开始时间和最晚开始时间,但是如果有环的话,那么就导致事件无限循环无法结束,最终报错–>至于通过报错判断是否有环是否可以利用还存在争议
深度优先遍历
深度优先遍历如何判断有向环是否有环?
基于深度优先遍历,如果只是用来遍历每个结点而不重复,那么会给每个遍历过的结点标记为1,弹栈后标记依旧存在,于是这遍历过的结点会影响其他深度的继续前进。导致不会有重复的出现。
但是如果通过深度优先遍历来判断有向图是否有环的话,就要在标记1的基础上,给每次弹栈之后的顶点去掉标记(类比为真正意义上的弹栈)。至于为什么要这样做?
因为首先要搞清楚对于有向图环究竟是什么?就是对一条路径上探索到最深处而不出现首位相连的情况。因此只需满足该次递归直到结束,过程之中不会出现重复顶点即可,如果不清除标记,那么被访问过的顶点如果同时出现在其他深度的递归里面,那么该深度的前进就会碰到所谓”重复的顶点”,但是其实并没有在该条递归中重复出现(并没有环),那么就无法判断是否有环了。
下面是一个有向图无环图。从深度优先1–>2–>4,弹栈回到1–>3–>4.在各自的栈内都没有重复元素,说明无环存在。
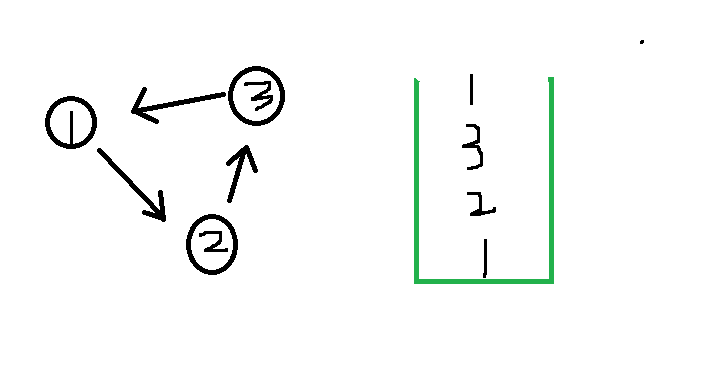
下面是一个有向环图,深度优先从1–>2–>3–>1,发现重复元素,说明有环存在。
广度优先遍历
广度优先遍历无法判断是否有环存在
为什么广度优先遍历不能判断有向图是否有环存在呢?
因为广度优先遍历是按照图的层次结构,从起始顶点开始,依次访问与它相邻的所有顶点,然后再访问这些顶点的邻接点,直到所有顶点都被访问为止。在这个过程中,如果一个顶点有一条边指向已经访问过的顶点,并不能说明这两个顶点在同一个环中,因为它们可能是不同层次的顶点。
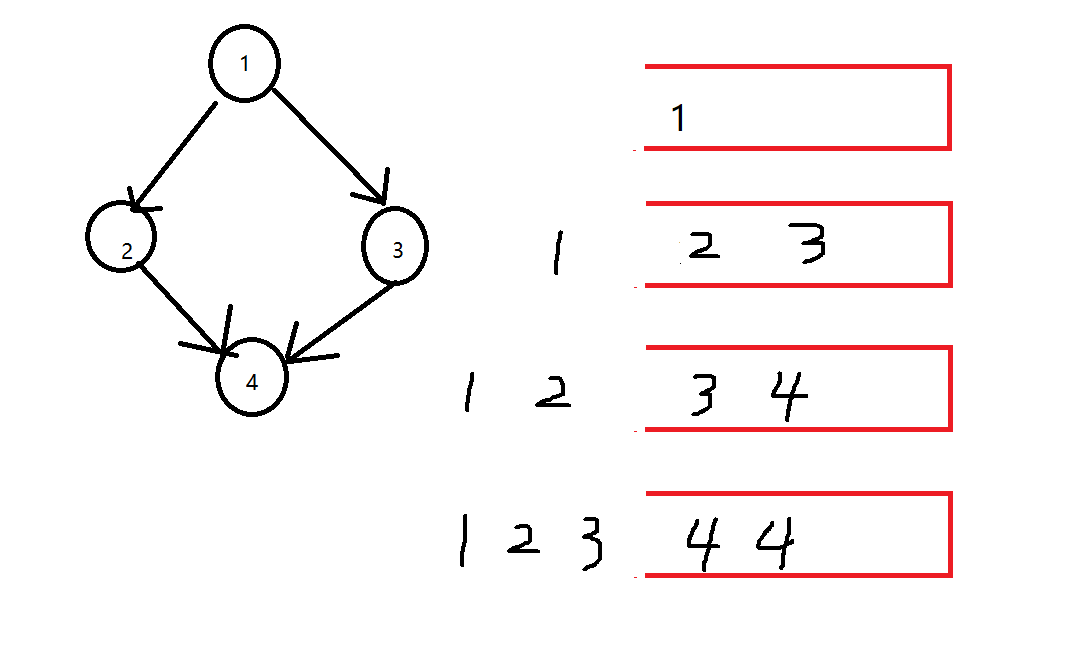
举下面的例子,每次入栈前都对顶点做了标记,发现,广度遍历对于无环图,也判断为遇到了重复顶点,因此广度优先遍历无法区分有向图的有环情况